Характерным для описания процессов передачи данных пакетным трафиком являются обнаруженные на практике свойства самоподобия, которые называют фрактальными процессами.
В случае самоподобного трафика при расчете параметров качества обслуживания трудно получить аналитически обоснованные результаты характеристик систем массового обслуживания в силу непредсказуемости самоподобных потоков. Кроме того, доказано, что на параметры качества обслуживания влияют и вероятностные законы распределения длительности обслуживания [1]. В работах [2, 3] показано, что исследование данной проблемы представляется важным, поскольку при наличии самоподобного трафика в системах передачи, как правило, ухудшается качество обслуживания по сравнению с тем, которое наблюдалось бы, например, в случае потока с пуассоновским распределением. Поэтому, вопросы исследования трафика с непуассоновкими функциями распределениями вероятностей длительностей поступления и обслуживания остаются актуальными.
Цель исследования
При решении таких задач, в современных телекоммуникационных сетях, трафик описывается с помощью распределений с «тяжелыми хвостами», которые приводят к самоподобным процессам [2, 4]. Для анализа выбираем наиболее встречающиеся распределения с «тяжелым хвостом» – Вейбулла и Парето. Используя данные распределения можно смоделировать систему массового обслуживания типа G/G/1, которая наиболее адекватно описывает работу любого сетевого элемента, и исследовать характеристики реального трафика.
С учетом вышесказанного, одной из целей исследования является аппроксимация неизвестной функции плотности распределения вероятностей, описывающей закон длительности поступления пакетов и обслуживания в узле связи. Поиск метода аппроксимации функции сводится к получению приближающейся кривой, которая полностью будет удовлетворять и, с наименьшей погрешностью, описывать фиксированные параметры трафика.
Определена задача исследования непуассоновского трафика посредством поиска функции, которая аппроксимирует неизвестные функции плотности распределения вероятностей времен, поступающих и обслуживаемых запросов внутри сетевого устройства. Необходимо, чтобы аппроксимирующее выражение удовлетворяло свойствам функции плотности распределения случайной величины, расчет его производился быстро и рационально, а метод аппроксимации имел простой алгоритм.
Методы исследования и их сравнительный анализ
Задача аппроксимации функции произвольного распределения вероятностей сводится к тому, чтобы оно имело рациональное преобразование Лапласа [5] и численное решение интегрального уравнения Линдли [6, 7].
В качестве видов аппроксимации распределений рассмотрены следующие методы:
- кумулянтный анализ;
- метод Прони;
- аппроксимация суммой затухающих экспонент;
- селектирующие функции.
Ф. Эджвортом [8] были введены одноименные ряды, а их асимптотические свойства исследованы Г. Крамером, который показал, что при довольно общих условиях ряд Эджворта дает асимптотическое разложение плотности распределения с остаточным членом порядка первого отброшенного члена.
Применение кумулянтного анализа для аппроксимации функций плотности распределения вероятностей и возможность представления функций через кумулянты позволяют получить аппроксимирующее выражение плотности распределения вероятностей на выходе обрабатывающего устройства и построить соответствующий график.
Кумулянты случайной величины, являющиеся коэффициентами разложения логарифма характеристической функции случайной величины в степенной ряд, определяются формулой (1).
(1)
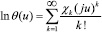
Для решения поставленной задачи были рассмотрены первые четыре коэффициента.
В результате проведенного анализа [9,4] было выявлено, что в случае произвольных потоков расчет средних значений характеристик обслуживания заявок обычно проводится на основе аппроксимации закона распределения интервалов времени между заявками в потоке с учетом первых двух моментов. Такой подход особенно широко используется при разработке приближенных методов расчета неэкспоненциальных систем массового обслуживания. Однако, как показывают исследования, если для расчета характеристик функционирования системы на уровне средних значений, в частности, среднего времени ожидания заявок в очереди, достаточно задать только два момента длительности обслуживания, то при описании интервалов времени между заявками в потоке этого оказывается недостаточно. Другими словами, на средние значения характеристик обслуживания заявок оказывают существенное влияние моменты более высокого порядка [10, 11].
Следовательно, кумулянтный анализ может применяться для решения задач только с определенными ограничениями и условиями обработки, учитывающими погрешность приближенного значения аппроксимирующей функции [12, 13]. Таким образом, аппроксимация функций плотностей распределения вероятностей интервалов времени между поступлениями пакетов на вход обрабатывающего устройства и распределения вероятностей длительности обслуживания пакетов с помощью ряда Эджворта возможна при некоторых ограничивающих условиях.
Для случая, когда функция плотности распределения вероятностей задается в численной форме, одним из подходящих методов является метод Прони [7, 14, 15], осуществляющий моделирование выборочных данных в виде линейной комбинации экспоненциальных функций. С помощью данного метода осуществляется аппроксимация функций с использованием некоторой детерминированной экспоненциальной модели [16]. Анализ аппроксимации функций плотностей распределения вероятностей интервалов времени между поступлениями пакетов на вход обрабатывающего устройства и распределения вероятностей длительности обслуживания пакетов с помощью метода Прони показывает, что аппроксимация является удовлетворительной при условии вещественных и отрицательных показателей экспонент.
В силу невозможности использования выше перечисленных методов для аппроксимации распределений с «тяжелыми хвостами», без наложения ограничений на условия начальных параметров, был разработан метод аппроксимации суммой затухающих экспонент. При этом методе существенным было выполнение требования наличия показателей экспонент, которые являются вещественными и отрицательными при положительных значениях аргумента. На рисунке 1 показан пример данного вида аппроксимации при распределении Вейбулла.
Рис. 1. Сравнение двух плотностей распределения Вейбулла при аппроксимации суммой затухающих экспонент
На данный момент, в результате проведенных исследований, определено, что для распределений, существующих на отрезке около нуля, предложенный метод аппроксимации распределения суммой затухающих экспонент даёт неудовлетворительные результаты по точности аппроксимации на «восходящих» ветвях распределений. Кроме того, аппроксимация «восходящих» ветвей распределений приводит к появлению в сумме затухающих экспонент слагаемых с отрицательными коэффициентами, что нивелирует вычислительные преимущества спектрального метода, обусловленные использованием гиперэкспоненциальных распределений.
Таким образом, было предложено представить функцию в виде «сшитой» функции через кусочно - нелинейные ϕ1(x) и ϕ2(x)(2).
(2)
Такая аппроксимация должна обладать существенно меньшей погрешностью, по сравнению со случаем, когда используется единая аппроксимация распределения суммой затухающих экспонент, так как функции рассматриваются на обоих участках отдельно (на участке около нуля – аппроксимация полиномом, на участке «тяжелого хвоста» – аппроксимация суммой затухающих экспонент), а затем результаты объединяются или «сшиваются» для адекватного представления аппроксимации распределения в целом.
Выводы
Представленный анализ служит начальным этапом для исследования сетевых параметров и разработки моделей, учитывающих реальный характер пакетного трафика и детали его обслуживания в сетевом устройстве для разных коммуникационных приложений, что является приоритетным вопросом при анализе и прогнозировании сетевого трафика.

