В работах [1,3,4] описана термостимулированная ЭДС, возникающая только в высоколегированном железом кристалле ниобата лития с напыленными электродами из пары различных металлов. Знак термоэдс определяется положением электродов, нанесенных напылением в вакууме на противоположные грани кристалла, и не зависит от ориентации кристаллографических осей образца относительно электродов.
Исследование природы данного явления является актуальным, поскольку твердотельные электрохимические источники эдс являются наиболее востребованными источниками энергии для микроэлектронной промышленности [9-11].
В данной работе анализируется электродинамическая модель данного явления. В данной работе приведены результаты экспериментального исследования термостимулированных токов в тонкослойной структуре металл – ниобат лития – металл.
В предлагаемой модели МСМ-структура рассматривается в качестве источника ЭДС с внутренним сопротивлением, равным сопротивлению кристалла. При этом зависимость термостимулированной ЭДС от температуры определяется температурной зависимостью сопротивления полупроводникового кристалла Rкр.
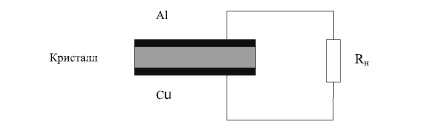
Рис. 1. Схема включения кристалла в измерительную цепь
В предлагаемой модели МСМ-структура рассматривается в качестве источника ЭДС с внутренним сопротивлением, равным сопротивлению кристалла. При этом зависимость термостимулированной ЭДС от температуры определяется температурной зависимостью сопротивления полупроводникового кристалла Rкр.
Экспериментально измерялся коэффициент
где Un- напряжение на нагрузке, T- температура кристалла, Rn- сопротивление нагрузки, S-площадь электрода кристалла. Из закона Ома имеем:
(1)
где E0- электретная ЭДС, Rk-сопротивле-ние кристалла. Отсюда для коэффициента Pel получаем:
(2)
где ρ-удельное сопротивление кристалла, L-толщина кристалла, ρꞌ-производная удельного сопротивления кристалла по температуре,
Согласно работе [2] температурная зависимость удельного сопротивления кристаллов ниобата лития, легированных железом с концентрацией более 0.3 вес. % (для которых в [2] были получены основные экспериментальные результаты), описывается законом Мотта:
(3)
где ρo, ,To - эмпирические константы, зависящие от концентрации легирующей примеси. Из (3) получаем:
(4)
Окончательно имеем для тока на нагрузке и коэффициента Pel :
Сопоставление полученных аналитических зависимостей с экспериментальными позволяет проверить адекватность модели.
Для анализа модели использовалась линейная аппроксимация экспериментальных зависимостей величины Pel от геометрии и температуры кристалла, концентрации легирующей примеси.
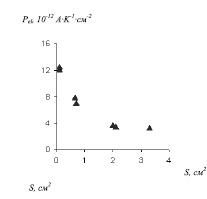
Рассмотрим зависимость Pel от площади одного из двух электродов, нанесенных на противоположные грани кристалла - Рис.2. Приводя (6) к линейной функции, получаем следующее выражение:
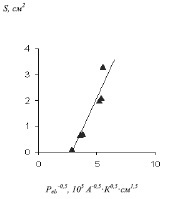
Экспериментальные данные (Рис.2а) в линеаризованных координатах согласно формуле (7) показаны на Рис.2б. Прямая соответствует численной аппроксимации выражения (7) по методу наименьших квадратов.
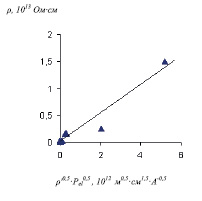
Величина удельного сопротивления определенного из рисунков 2-3 составляет 7*109 - 1010 Ом*см соответственно, что по порядку величины близко к значениям, полученным в работе [328 ]-109*1010 Ом* см.
Из этих же графиков можно получить значение параметра E0ρꞌ, который составляет величину около 109 В* Ом*см* К-1
Подставляя значение ρꞌ =1011 Ом*см* К-1, имеем оценку E0=10-3 В.
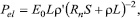
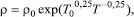
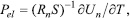
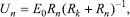
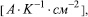
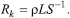
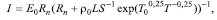
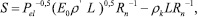
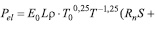
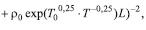
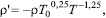
а) б)
Рис. 2. Экспериментальная зависимость коэффициента Pel от площади электрода S
(L =1 мм; 0,3 вес.% Fe; электроды Al-Cr) - 2а; линейная аппроксимация согласно формуле (7) – 2б. Критерий R2 =0,95; E=0,0013 В.
а) б)
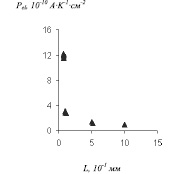
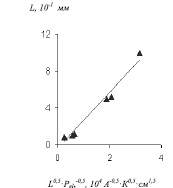
Рис. 3. Экспериментальная зависимость коэффициента Pel от толщины кристалла L (S=5мм2; 0,3 вес.% Fe; электроды Al-Cr)- 3а; линейная аппроксимация согласно формуле (8) Критерий R2 =0,99; E=0,0085 В
а) б)
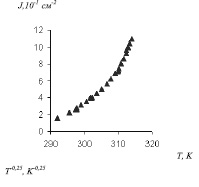
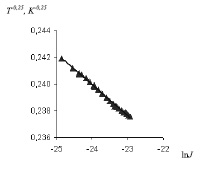
Рис. 4. Экспериментальная зависимость плотности тока от температуры кристалла (LiNbO3:Fe – 0,43 вес.%, 10x5x1мм3, Y – срез; Al – Cr) и линейная аппроксимация согласно формуле (9); Критерий R2 =0,99
а) б)
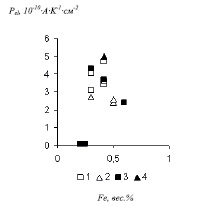
Рис. 5. Экспериментальная зависимость коэффициента Pel, от концентрации примеси железа в кристалле ниобата лития для разных срезов и материалов контактов(1–Al–Cr, Z -cрез; 2 – In – Cr, Z – срез;3–Al–Cr, Y – срез; 4 – In – Cr, Y – срез) и линейная аппроксимация зависимости ρ’0,5·Pel0,5 согласно формуле ( ). Критерий R2 =0,93
Аналогично, линеаризуя зависимость Pel от толщины кристалла (Рис.3а.), получаем:
(8)
Соответствующий график представлен на Рис.3б
На рисунке 4 показана экспериментальная зависимость плотности термостимулированного тока от температуры кристалла. Данную зависимость можно так же аппроксимировать линеаризованной функцией , полученной из формулы (5.15):
(9)
Из рисунков 2-4 видно, что экспериментальные зависимости достаточно близки к линейным, что свидетельствует в пользу предлагаемой модели.
Концентрационная зависимость коэффициентаPel (Рис.5) так же может быть обусловлена зависимостью ρꞌ- и ρ- от процентного содержания легирующей примеси.
Таким образом проведенное сравнение экспериментальных данных и численных расчетов на основе электретной модели демонстрирует неплохое качественное и количественное соответствие. Небольшие отклонения расчетных и экспериментальных данных наблюдаются в области малых толщин МСМ-структуры, что может быть связано с влиянием контактных явлений. Более корректное определение величины термоэлектретной ЭДС требует точных экспериментальных значений ρꞌ- и ρ- исследуемых образцов.
В данной работе предложена термохимическая модель исследуемого явления, обусловленного полем контактной разности потенциалов на границах раздела металл – сегнетоэлектрик. Предполагается, что появление тока вызвано появлением разности потенциалов в области контакта электрод – кристалл. В случае одинаковых материалов электродов контактные разности потенциалов равны и противоположно направлены. Тогда результирующая ЭДС равна нулю.
Полученные результаты можно использовать для разработки приемников излучения [5-8], а также при интерпретации экспериментальных результатов по изучению свойств сэндвичных пироэлектрических структур [12-15].

