Scientific journal
International Journal of Applied and fundamental research
ISSN 1996-3955
ИФ РИНЦ = 0,593

Personal portfolio

 §1. Постановка задачи.

Будем рассматривать дифференциальное уравнение шестого порядка следующего вида:

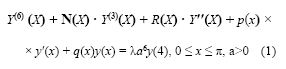
где коэффициенты ν(x), r(x), p(x) и q(x) в дифференциальном уравнении (1) являются суммируемыми функциями, то есть удовлетворяют условиям теоремы Римана-Лебега:

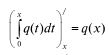 почти всюду ∀x ∈ [0; π]

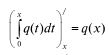почти всюду и т.д.

В диффер. уравнении (1) число λ является спектральным параметром. Цель статьи — найти асимптотику решений дифференциального уравнения (1) при больших значениях спектрального параметра λ.

§2.Асимптотика решений дифференци-ального уравнения (1). Пусть λ = s6, s =6√  — некоторая фиксированная ветвь корня (мы её выберем условием 6√1 =+1 ). Пусть ωk, (k = 1, 2, …,6) — различные корни шестой степени из единицы: ω6k = 1,

Про числа ωk известны следующие свойства:

Методами работ [1] и [2] доказывается следующая теорема. Теорема 1. Решение дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерра

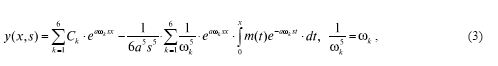
при этом в силу свойства (2) имеем:

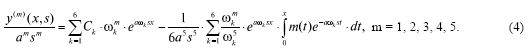
где m(x) + ν(x) · y(3)(x) + r(x) · y"(x) + + p(x) · y′(x) + q(x) · y(x), Ck (k = 1, 2, …, 6) — произвольные постоянные.

Доказательство теоремы 1 заключается в подстановке формулы (4) (при m = 5) и (3) в уравнение (1) с использованием свойства (2).

Далее применим метод последовательных итераций Пикара. Находим y(t, s) из (3) и y(m) (t, s), (m = 1, 2, 3) из (4) и снова подставим в интегральное уравнение (3). Затем произведём необходимые оценки, аналогичные оценкам монографий [2] и [3]. При этом приходим к выводу, что справедливо следующее утверждение.

 Теорема 2. Общее решение дифференциального уравнения (1) имеет следующий вид:

где Ck — произвольные постоянные, причём фундаментальная система решений {yk(x,s)}6 k=1  допускает следующие асимптоти-ческие оценки при |s|→+∞:

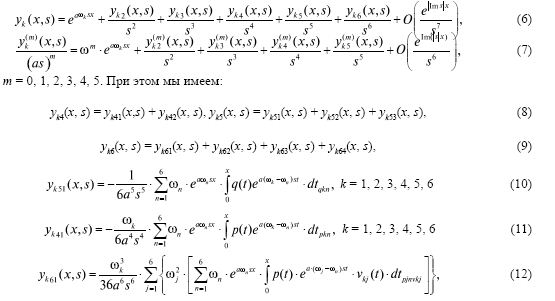
причём в формуле (10) (и дальше) введено следующее обозначение:

 

Процесс итераций нам пришлось применять трижды.

Асимптотика решений дифференциального уравнения (1) при выполнении условий суммируемости коэффициентов полностью получена в формулах (5)-(23). Теорема 2 доказана.

Аналогичная методика применялась автором данной статьи для нахождения асимптотики решений дифференциальных уравнений второго и четвёртого порядка в работах [4, 5].

Другим методом была получена асимптотика решений дифференциального уравнения второго порядка в классической работе В.А. Садовничего и В.А. Винокурова [6]. Их методика на операторы порядка выше второго не переносится.

Список литературы

  1. Наймарк М.А. Линейные дифференциальные операторы. - М.: Наука, 1969. - 528 с.
  2. Юрко В.А. Введение в спектральную теорию. - М.: Физматлит, 2007.
  3. Левитан Б.М., Саргсян И.С. Введение в спектральную теорию. - М.: Наука, 1970.
  4. Митрохин С.И. Асимптотика собственных значений дифференциального оператора четвертого порядка с суммируемыми коэффициентами // Вестник Моск. ун-та. Сер.1, математика, механика. - 2009. - №3. - С. 14-17.
  5. Митрохин С.И. О спектральных свойствах дифференциального оператора с суммируемым потенциалом и гладкой весовой функцией // Вестник СамГУ - естественнонаучная серия. - 2008. - №8/1(67). - С. 172-187.
  6. Винокуров  В.А.,  Садовничий  В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. -2000. - Т. 64, №4. - С. 47-108.