В настоящее время во всех разделах медицины активно используются различные математические методы. Они охватывают широкий круг вопросов, начиная с обработки данных и заканчивая построением математических моделей, описывающих различные процессы, протекающие в живом организме. Обучение будущих врачей математическим основам медицинских знаний в первую очередь должно быть направлено на получение высококвалифицированных специалистов, которые способны применять полученные математические знания для решения проблем профессиональной направленности. Стоит отметить, что особую ценность представляют не конкретные математические знания, полученные студентами медицинского вуза, а умение использовать их для достижения учебных, диагностических, лечебных целей, применять при использовании вычислительной техники и различного программного обеспечения. Также изучение математики способствует формированию не только профессиональных, но и многих общекультурных компетенций, которые необходимы специалисту любой профессии: способность логически мыслить, систематизировать и анализировать информацию, четко ставить цели, строить причинно-следственные связи [2].
На данный момент в медицинских вузах изучается дисциплина «Физика, математика», которая согласно ФГОС ВО включена в базовую часть математического, естественнонаучного и медико-биологического циклов. Студентами лечебного, педиатрического, стоматологического факультетов математика изучается на первом курсе, когда они имеют еще слабое представление о дальнейшей профессиональной деятельности и тех знаниях, которые им будут необходимы. На изучение дисциплины «Физика, математика» отводится 3 зачетные единицы (108 академических часов). Из них на аудиторную работу приходится 73 часа (68%), из которых на математику отводится 16 часов (21%): 4 часа лекционных и 12 часов практических занятий [4].
На основе интегративно-модульного подхода в русле ФГОС ВО нами был разработан курс математики в рамках изучаемой дисциплины «Физика, математика». В данном курсе нами выделены два модуля: Модуль 1 «Теория вероятностей» и Модуль 2 «Математическая статистика».
Теория вероятностей играет важную роль в профессиональной деятельности врача. Одной из профессиональных компетенций является способность и готовность к постановке диагноза (ПК 15). Врач на основании имеющейся информации всегда делает прогноз, что в свою очередь имеет вероятностный характер.
Основные цели курса при изучении теории вероятностей заключаются в следующем: ознакомить студентов с широким кругом понятий теории вероятностей; сформировать у них терминологический запас, необходимый для самостоятельного изучения литературы; выработать у студентов умения практического использования теоретико-вероятностных моделей.
Математическая статистика является прикладной частью теории вероятностей и направлена на обработку экспериментальных данных, анализ и грамотная интерпретация которых, помогают в принятии правильного решения. Математическая статистика использует все основные понятия, законы и методы теории вероятностей.
Основные цели, которые ставятся перед студентами медицинского вуза при изучении методов математической статистики заключаются в следующем: сформировать у студентов основной понятийный аппарат необходимый для обработки данных, научить правильно формулировать цель статистического исследования, выбирать соответствующие методы статистической обработки результатов, анализировать полученные данные. Изучив основные понятия и понимая схему расчета нужного показателя, студенты приступают к решению практических задач, которые играют важную роль в актуализации математических знаний.
В каждом из модулей нами выделены как инвариантная, так и вариативная части курса. Для достижения поставленных целей, вариативная часть курса математики в рамках интегративно-модульного подхода включает в себя задачи профессиональной направленности. Приведем пример, который показывает, как с помощью формулы Байеса можно формализовать логику врача при постановке диагноза [3]:
Пример 1. Пусть врач при первичном осмотре больного предполагает три диагноза: H1, H2, H3. Вероятности наличия у больного этих диагнозов, по-мнению врача, распределяются следующим образом P(H1)=0,5; P(H2)=0,17; P(H3)=0,33. Основываясь на результатах осмотра, врач предполагает первый диагноз. Для его уточнения назначаются дополнительные исследования, например, анализ СОЭ (событие A). Вероятности увеличения СОЭ при каждом из предполагаемых заболеваний заранее известны:
P(A/H1)=0,1; P(A/H2)=0,2; P(A/H3)=0,9.
Результаты анализа показали увеличение исследуемого показателя. Используя формулу Байеса (в условиях нашей задачи n=3), найдем вероятности предполагаемых заболеваний с учетом новой информации (у пациента наблюдается увеличение СОЭ – событие A произошло):
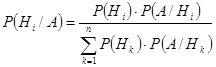
В результате вычислений получены следующие значения вероятностей: P(H1/A)=0,13, P(H2/A)=0,09, P(H3/A)=0,78.
Учитывая новую информацию, врач делает вывод о том, что у больного, скорее всего, третий диагноз, вероятность которого резко увеличилась в связи с получением новых данных.
Математические задачи, моделирующие профессиональную деятельность, предполагают, что студенты хорошо ориентируются и в смежных дисциплинах.
Рассмотрим задачу следующего вида [1]:
Пример 2. Пусть надежность определения туберкулеза при проведении рентгенологического исследования грудной клетки составляет 91% (т.е. 9% носителей туберкулеза остаются не выявленными). Вероятность того, что здоровому человеку ошибочно будет поставлен туберкулез – 1%. Рентгенологическому исследованию была подвергнута большая группа людей со средним процентом больных 0,0002%. Найдите вероятность того, что человек, признанный больным, действительно является носителем туберкулеза.
Эта задача также решается с помощью формулы Байеса. Задача предполагает, что студенты знают не только теорию вероятностей и математическую статистику, но и физику.
Медицинские работники в современных условиях постоянно сталкиваются с различными статистическими данными, поэтому в рамках модуля «Математическая статистика» студентам предлагаются задачи, в которых они должны не только принять правильное решение об использовании того или иного статистического метода, но и применить соответствующие компьютерные программы для расчета необходимых показателей. Также студенты учатся правильно интерпретировать и грамотно представлять полученные результаты.
Использование задач профессиональной направленности, где к выполнению задания нужно подойти творчески и интегрировать знания из смежных областей, помогают студентам взглянуть на курс математики с другой стороны, увидеть, что математика – интересный и многогранный предмет. Анкетирование, проводимое на первом курсе, это подтверждает.
Опрос студентов лечебного факультета в начале семестра, до изучения дисциплины, показал, что математика для них является неинтересным предметом. Из 196 опрошенных 60 человек (31%) не видят смысла изучать математику в медицинском вузе, а единственный мотив к ее изучению в школе – «сдать базовый уровень ЕГЭ». Причем эта цифра сохраняется на протяжении нескольких лет.
Использование же задач по математике, связанных с профессиональной деятельностью, способствует развитию познавательного интереса будущих медиков (об этом говорят 86 % опрошенных), а это, в свою очередь, повышает их успеваемость. Студенты больше уделяют времени самостоятельной подготовке, что особенно важно в условиях малого количества часов, отводимых на изучение дисциплины.

