Транспортный поток представляет собой совокупность движущих средств. Загрязнения от автотранспорта негативно влияет на здоровье человека и окружающую среду. Среди негативного влияния особое значение имеет: загрязнение воздуха (окислами углерода СО, углеводородами СmНn, окислами азота (NO, NO2), соединениями свинца, канцерогенными веществами, сажей, альдегидами, которые могут сократить продолжительность жизни до 9 лет); шумовые загрязнения (приводят к нарушению сна, развитию гипертонии и ишемической болезни сердца, снижают производительность труда, что может сократить продолжительность жизни до 12 лет). В 2000 г. в Российской Федерации автотранспорт выбросил в атмосферу 11824,2 тыс.т. выхлопных газов. В тоже время без транспорта не может обойтись экономика любой страны. Чтобы как-то уменьшить негативное влияние транспорта на окружающую среду, исследователи всего мира стремятся найти оптимальное движение транспортного потока и самого транспорта с целью уменьшения выхлопных газов, энергосбережения и других ресурсов. В результате наблюдений и обобщения таких исследований строятся математические модели транспортного потока. Математические базовые модели транспортного потока, это те модели, которые являются фундаментальными. Базовые модели с течением времени модифицируются, путем уточнения или незначительного добавления параметров (факторов). Добавление, уточнение параметров фундаментальных моделей транспортного потока увеличивает разнообразие, создает дочерние модели, делает их более адекватными [1, 2, 3, 4, 5]. На рис. 1 показана классификация основных базовых моделей транспортного потока:
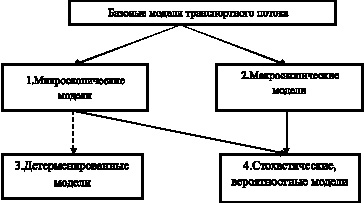
Базовые модели транспортного потока
Рассмотрим эти модели более подробно.
1. В Микроскопических моделях транспортного потока оперируют элементами потока – следующими друг за другом транспортные средства, которые имеют характерные физические параметры. Элемент потока реализуется на основе его физического представления. До предела упрощенную (условно) микроскопическую модель транспортного потока можно представить, например, в виде равенства (1):
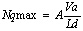 , (1)
, (1)
где Nqmax – максимально возможная интенсивность транспортного потока; A – коэффициент размерности (для согласования левой и правой части уравнения); Va – средняя скорость транспортного потока; Ld – средняя динамическая длина транспорта.
Именно в таком виде часто можно найти в литературе эту модель. Но если участь, что параметры Va и Ld относятся к характеристикам транспортного потока в целом, то лучше ее отнести к макроскопической модели транспортного потока.
2. Макроскопическая модель (не имеет элемент потока) основывается на уравнении неразрывности, которая описывает постоянство количества жидкости, притекающей через трубу. Базовую модель можно представить, например, в виде уравнений (2):
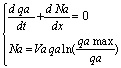 , (2)
, (2)
где Na – интенсивность транспортного потока; Va – скорость потока; qa –плотность транспортного потока; qa max – плотность транспортного потока при заторе.
Базовая модель может иметь и другой вид по аналогии с жидкостью, включающая факторы состояния среды, в которой движется поток, состояние дороги и даже водителей.
3. Детерминированная модель – модель, в которой имеется функциональная однозначная зависимость между отдельными показателями функции. Модель (1) часто называют детерминированной. В реальности входящие составляющие модели Va, Ld являются вероятностными (стохастическими). И сама модель больше относится к стохастической. Микроскопическая детерминированная модель должна строиться на основе физического представления транспортного средства, где имеются конкретные связи между параметрами элемента транспортного потока и всего транспортного потока. В модели (1) этого нет. В связи, с чем модель (1) назвали условно микроскопической детерминированной (на рисунке показана пунктирная стрелка). Микроскопические детерминированные модели в основном разрабатывались в науке человечества в XVII, XVII и XIX веках, а в XX, XXI их появляется относительно крайне мало. В то же время, в частности микроскопическая модель транспортного потока, нужна для глубокого понимания и расчетов транспортных потоков с целью экологической безопасности.
4. Базовые вероятностные (стохастические) модели часто строятся на известных («стандартных») зависимостях, например на уравнении (распределении) Пуассона (для однородного потока машин)
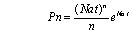 , (3)
, (3)
где Pn(t) вероятность проезда n-го числа автомобилей за время t; Na – основной параметр распределения (интенсивность транспортного потока) авт./с; t – длительность отрезков наблюдения, с; n – число наблюдаемых транспортных средств.
Сравнительная характеристика моделей транспортного потока
|
Наименование модели транспортного потока |
Достоинства |
Недостатки |
|
|
Микроскопическая модель транспортного потока |
Детер-мини-рованная |
1. Имеет наглядную связь между параметрами (режимом работы) транспортных средств и параметрами транспортного потока. 2. Можно учитывать влияние параметров элемента – транспортного средства на транспортный поток в целом. |
1. Как правило, модель получается громоздкой. 2. Требуются очень большие вычислительные ресурсы. |
|
Стоха-стическая |
1. Простота модели 2. Требеются малые («стандартные») вычислительные ресурсы |
1. За простатой и «стандартностью» модели теряется физическая связь между параметрами модели |
|
|
Макроскопическая модель транспортного потока |
Стоха-стическая |
1. Простота модели 2. Требеются малые («стандартные») вычислительные ресурсы |
2. Не учитывается параметры и режимы работы элемента потока при расчете транспортного потока. |
Для смешанного транспортного потока (грузовые, легковые и т.д.) рекомендуется использовать уравнения гамма-распределение Пирсона III типа или распределение Эрланга. Описанные выше вероятностные модели в основном используют как однофакторные.
Для построения многофакторных стохастических моделей лучше всего использовать регрессионные модели. Например, простейшая многофакторная модель транспортного потока представлена формулой (4):
Na = A1 Val +A2 qa, (4)
где Na – интенсивность потока; Val – скорость потока; qa – плотность транспортного потока; А1, А2 – постоянные коэффициенты определяются методом регрессионного анализа из полученных экспериментальных данных.
Многофакторные (стохастические) модели более сложного вида в определенном интервале факторов могут давать достаточно точное описание транспортного потока, но не позволяют решить важнейшие проблемы, связанные с экологией и экономикой.
Макроскопические модели бывают только вероятностными.
Есть много моделей транспортного потока, которые появились (особенно за рубежом) буквально в течение последних нескольких десятилетий в связи с развитием вычислительной техники и программных средств (например, модели, построенные на основе объектно-ориентированного программирования). Такие модели в этой статье не рассматриваются.

