В настоящее время возросла потребность в современных информационных системах, в основе которых различные математические модели. Создание математических моделей диагностирования с применением методов принятия решений на основе нечетких множеств является перспективным направлением в медицине [1-3]. Применение достижений теории нечетких множеств является оправданной. Человек, обладая огромной функциональной энтропией, способен обрабатывать нечеткую информацию: выбирать, решать, анализировать и т.д., при этом может допустить субъективизм в своих суждениях. В этом плане создание математических моделей диагностирования и прогнозирования, повышающие объективность, является актуальной.
Применим для диагностики математический метод, на основе композиционного правила агрегирования описаний альтернатив, заданных в виде нечетких суждений и выбрать наилучший из них [4]. Пусть имеем U – множество элементов, А – его нечеткое подмножество, степень принадлежности элементов которого есть число из единичного интервала [0,1]. Подмножество А является значениями лингвистической переменной Х. Например: переменная Х – «заболеваемость» может иметь значение – «низкая», а Х – «анамнез» – значение «хорошее» и т.п. Высказывание S – «возможно», также является лингвистической переменной. В общем случае:
Di: «если Х1 = A1i и Х2 = А2i и … Хр = Арi, то S = Bi».
Обозначим переменные:
Х1 = А1 ∩ Х2 = А2 ∩ … Хn = Api через Х = Аi
Операции пересечения нечетких множеств соответствует нахождению минимума их функции принадлежности :
µАi(U) = min(µАi1(U), µАi2(U), … , µАрi(U))
µАij(Uj) – значение принадлежности элемента (Uj) нечеткому множеству Аij
Можно записать в виде:
Di: «Если Х = Аi, то S = Bi»
На основании диагностической таблицы [5] проводится дифференциация форм хронического энтерита в зависимости от локализации поражения тонкой кишки: преимущественное поражение тощей кишки (еонит) и преимущественное поражение подвздошной кишки (илент). В качестве признаков выступают симптомы: частота стула в сутки, вид кала, повышенное выделение желчных кислот с калом, тест с холестирамином, функциональный демпинг-синдром и т.д. Возьмем следующие критерии: частота стула в сутки – Х1, вид кала – Х2, повышенное выделение желчных кислот с калом – Х3, положительный тест с холестирамином – Х4, как симптомы наблюдаемые у условного пациента. Приемлемость решений – Y: «возможно», «более, чем возможно», «высокая вероятность» и т.д. задана на множестве j [0,1, 0.2, 0.3, … , 1] и определен как:
S – «возможно» – 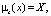 X∈j
X∈j
MS – «более чем возможно» – 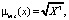 X∈j
X∈j
P – «очень высокая вероятность» – 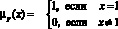 , X∈j
, X∈j
NS – «вполне возможно» – 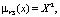 X∈j
X∈j
US –«отрицательный» – 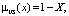 X∈j.
X∈j.
Введем оценку каждого состояния:
А = «частота стула в сутки 6-8 раз» = 0.7/u1; 0.5/u2; 0.5/u3; 0.6/u4; 0.3/u5
B = «вид кала водянисто-пенистый» = 0.8/u1; 0.9/u2; 0.3/u3; 0.7/u4; 0.9/u5;
C = «повышенное выделение желчных кислот с калом» = 0.5/u1; 0.7/u2; 0.5/u3; 0.8/u4; 0.3/u5;
D = «явно повышенное выделение желчных кислот с калом» = 0.4/u1; 0.5/u2; 0.3/u3; 0.5/u4; 0.6/u5;
Е = «Положительный тест с холестирамином» = 0.5/u1; 0.6/u2; 0.7/u3; 0.7/u4; 0.5/u5.
Тогда:
D1: если Х = А и В, то Y = S то есть «Если частота стула в сутки 6-8 раз и вид кала водянисто-пенистый, то Y = возможно у него «иленет»».
Аналогично:
D2: если Х = А и В и С , то Y = MS
D3: если Х = А и В и С и Е, то Y = P
D4: если Х = А и В и Д, то Y = NS
D5: если Х = не А или не В или не Е, то Y = US
Используем правило минимизации:
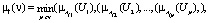
где 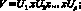
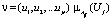
значения принадлежности элемента (Uj) нечеткому множеству Aij,
для:
D1: 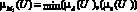
М1 = {0.7/u1; 05/u2 ; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5 }
D2: 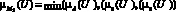
М2 = {0.5/u1; 05/u2; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5 }
D3: 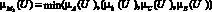
М3 = {0.5/u1; 05/u2 ; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5}
D4: 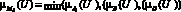
М4 = {0.4/u1; 05/u2 ; 0.3/ u3 ; 0.5/ u4 ; 0.3/ u5}
D5: 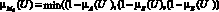
М5 = 
М5 = {0.5/u1; 05/u2 ; 0.7/u3 ; 0.4/u4 ; 0.7/u5}
D1: если х = М1 , то Y = S (возможно «илинет»). Переменная Y задано: j (0,0.1, …, 1), определено как 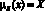 x∈j
x∈j
D2: если х = М2, то Y = МS (более чем возможно) 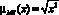 x∈j
x∈j
D3: если х = М3, то Y = Р (очень высокая вероятность) 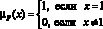
D4: если х = М4 , то Y = NS (вполне возможно) 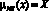 x∈j
x∈j
D5: если х = М5, то Y = US (невозможно, отсутствует) 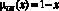 x∈j
x∈j
М1 = {0.7/u1; 05/u2 ; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5}
М2 = {0.5/u1; 05/u2 ; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5}
М3 = {0.5/u1; 05/u2 ; 0.3/ u3 ; 0.6/ u4 ; 0.3/ u5}
М4 = {0.4/u1; 05/u2 ; 0.3/ u3 ; 0.5/ u4 ; 0.3/ u5}
М5 = {0.5/u1; 05/u2 ; 0.7/u3 ; 0.4/u4 ; 0.7/u5}
Используя правило преобразования: «Если х = М1, то Y = Q» в выражении: 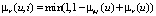 для каждой пары
для каждой пары 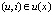 , получаем следующее нечеткое подмножество:
, получаем следующее нечеткое подмножество:

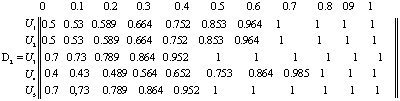



В результате получаем общее функциональное решение:
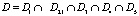 т.е.
т.е. 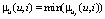

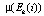
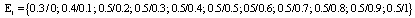
Находим: 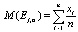 ,
, 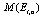 – мощность, где
– мощность, где 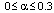 ,
, 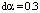
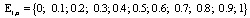 ,
, 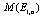 = 0.5
= 0.5
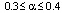 ,
, 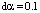
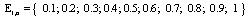 ,
, 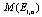 = 0.55
= 0.55
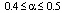 ,
, 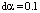
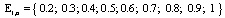 ,
, 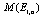 = 0.6
= 0.6
Найдем точечную оценку E1 :
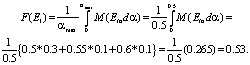
Аналогично для второй альтернативы:
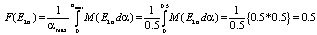
Для третьей альтернативы:
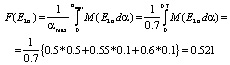
Для четвертой альтернативы:
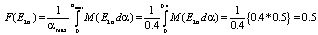
Для пятой альтернативы:
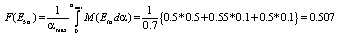
Итак, точечная оценка, найденная с учетом наличия симптомов и их заданных состояний, в качестве приемлемого вывода выбираем высказывание «возможно «иленет»», поскольку имеет наибольшее значение – 5.3. Данная математическая модель позволила из нечетких выводов, какими являются высказывания: «возможно», «более чем возможно», «очень высокая вероятность», «вполне возможно», «отрицательный» выбрать наилучший. Данная математическая модель диагностирования с использованием правила нечеткого вывода, наряду с другими моделями, основывающихся на достижениях теории нечетких множеств позволит, при соответствующей технической реализации, повысить объективность при принятий решений. Применение математического подхода к решению различных задач в медицинских исследованиях позволят более широко использовать современные автоматизированные информационные технологии в здравоохранении.

