Использование экспертных технологий в качестве инструмента для решения разнообразных задач широко применяется в различных сферах человеческой деятельности, в том числе в здравоохранении. Экспертные оценки признаны эффективным методом, используемым для принятия решений, прогнозирования и управления рисками, а теория и практика экспертных оценок представляется составной частью компетенций, необходимых для научных работников, руководителей и специалистов [1, 4, 5].
Большинство исследуемых объектов являются структурно и функционально сложными, поэтому их точное описание или оценка будет содержать множество цифровых и (или) выраженных по номинативной шкале показателей. Востребованность экспертных технологий связана с необходимостью получения исходных данных для математико-статистической обработки, которые могут быть получены либо как объективные результаты измерений в ходе наблюдения, опыта или других вариантов деятельности, либо как субъективные, но при этом комплексные и обобщающие мнения высококвалифицированных специалистов (экспертов), полезность и целесообразность использования которых доказана практикой [3, 4].
Разработка методов анализа экспертных мнений (оценок) способствовала развитию статистики широко применяющихся в исследованиях нечисловых данных – статистики объектов нечисловой природы, таких как, например, значения качественных признаков объектов экспертизы, выраженных при помощи кодировки с заданным перечнем градаций; упорядочения (ранжирования) экспертами объектов по степени проявления в них какой-либо характеристики; результаты парных сравнений по альтернативному признаку и ряд других.
При этом важно, чтобы условия проведения опроса способствовали получению достоверных данных, в связи с чем необходимо отметить ряд принципиальных аспектов. К данной категории условий следует отнести компетентность привлекаемых специалистов, полноту и четкость формулировки вопросов опросника, обеспечение независимости оценок путем устранения влияния на экспертов внешних факторов. Следует учитывать, также, что в процессе мышления человек оперирует образами, а не числами, а значит может вполне квалифицированно сравнить несколько объектов и ранжировать их по выраженности в них исследуемых показателей, измеренных по порядковой шкале. Последнее обстоятельство препятствует возможности корректно использовать среднюю арифметическую полученных показателей, что существенно ограничивает возможности исследователей по анализу и интерпретации данных.
В тех случаях, когда появляется потребность подобрать коэффициенты весомости (важности) для отдельных показателей для уточнения ранжирования, по литературным данным не рекомендуется оценивать указанные коэффициенты с помощью экспертов, которые не в состоянии выполнить данную функцию на приемлемом уровне [2, 3]. Эксперты, обычно, могут сравнить объекты в целом, в то же время, испытывают существенные затруднения при необходимости вычленить вклад отдельных факторов. В тех случаях, когда организаторы опроса спрашивают их об этом, эксперты отвечают, но «эти ответы не несут в себе надежной информации о реальности» [3].
Таким образом, имеется необходимость в усовершенствовании подходов при использовании экспертных опросов, вызванная, в частности, тем, что эксперты дают оценки прежде всего в порядковых шкалах и (или) в вербальной форме, что позволяет использовать метод ранжирования, однако препятствует корректно использовать варианты математико-статистической обработки показателей с применением средней арифметической, что значительно ограничивает возможности анализа и интерпретации полученных данных. Разработанная модель и технология экспертной количественной сопоставительной оценки объектов с использованием показателей интервальной шкалы представляет такую возможность.
В основу данной модели и технологии положено представление о том, что интервальные данные можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств (множество с нечеткими границами, когда переход от принадлежности элементов множеству к непринадлежности их множеству происходит постепенно). Так, если характеристическая функция нечеткого множества равна 1 на некотором интервале и равна 0 вне этого интервала, то задание нечеткого множества эквивалентно заданию интервала, то есть характеристическая функция множества может принимать любые значения в интервале от 0 до 1, а не только значения 0 или 1.
Если при этом для анализа нечисловых экспертных данных использовать методы классификации, адекватные цели исследования, основанные на использовании расстояний или показателей различия, то модель и технологию экспертной количественной сопоставительной оценки объектов с использованием показателей интервальной шкалы можно представить следующими инструментами измерения и алгоритмом деятельности.
1. Количественная оценка (в баллах) выраженности признака (явления) по показателям размаха в поименованной шкале.
Для этого экспертам на поименованной шкале от 1 до 9 баллов (см. рисунок) следует поставить две отметки, одна из которых обозначит оценку объекта с максимальным проявлением исследуемого признака (явления), а вторая с минимальным проявлением. Остальные оцениваемые объекты (если объектов более двух), будут предполагаться, по степени выраженности у них изучаемых признаков, в пределах этих двух, отмеченных показателей на шкале.
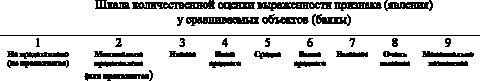
Шкала количественной оценки выраженности признака (явления)
2. Сопоставительная количественно-качественная оценка.
Далее следует заполнить таблицу «Количественно-качественная сопоставительная экспертная оценка объектов по уровню выраженности у них проявления исследуемого признака» (см. табл. 1), в которой каждый из оцениваемых объектов необходимо отнести к одной из трех групп – I, II, III, где номер группы означает соответственно – наличие наиболее высоких проявлений (выше среднего) оцениваемого признака в данной совокупности из числа всех сравниваемых объектов (I группа), далее следует определить объекты с минимальных проявлениями (ниже среднего) оцениваемого признака в данной совокупности средних (III группа) и, наконец с промежуточным (средним) уровнем проявлений оцениваемого признака (II группа).
Таблица 1
Вид таблицы «Количественно-качественная сопоставительная экспертная оценка объектов по уровню выраженности у них проявления исследуемого признака (явления)»
|
Позиции в группе |
Группы |
||
|
I |
II |
III |
|
|
1 Максимальное проявление признака в данной группе |
|||
|
2 среднее проявление признака в данной группе |
|||
|
3 Ниже среднего проявление признака в данной группе |
|||
После распределения всех оцениваемых объектов в соответствующие группы, внутри каждой группы следует разнести помещенные объекты по трем позициям в зависимости от проявления оцениваемых качеств объектов внутри рассматриваемой группы. В 1-ую позицию следует включить объекты, в которых выраженность качества (или проявления того, что оценивается) проявляется выше, чем у других объектов, входящих в эту группу. Соответственно в 3-ью позицию из всех входящих в данную группу объектов нужно включить те из них, выраженность проявления оцениваемого признака меньше, чем у всех входящих в данную группу. Оставшиеся войдут во 2-ую позицию данной группы.
Следуя предложенным рекомендация, получится, что при заполнении этой таблицы два объекта, из всех оцениваемых, всегда будут помещены в определенные ячейки. В ячейку I группы в позицию 1 помещается объект с максимальной выраженностью признака, – это тот объект, характеристика которого была основанием для максимальной оценки проявления признака на шкале количественной оценки выраженности признака (явления) среди всех сравниваемых объектов. Соответственно, в ячейку III группы в позицию 3 следует поместить объект с минимальной выраженность признака (явления). Остальные объекты будут располагаться между ними. При оценке обязательно заполнение всех 3 групп, т.к. ранжирование относительное.
Таким образом у экспертов имеется возможность ранжировать оцениваемые объекты не только по группам, но и внутри каждой из этих групп, а значит более точно соотнести каждый из объектов по степени выраженности у них исследуемых признаков.
3. Расчет количественных интервальных показателей на основе экспертной оценки и их ранжирование.
Вначале рассчитывается размах оценок сравниваемых (оцениваемых) признаков (явлений). Для этого из максимальной оценки, которую определили эксперты по «Шкале количественной оценки выраженности признака (явления) у сравниваемых объектов (баллы)» вычитается минимальная. Полученную разность следует разделить на 9 (это число ячеек в таблице «Количественно-качественная сопоставительная экспертная оценка объектов по уровню выраженности у них проявления исследуемого признака (явления)» (см. таблицу). Частное от деления представляет собой величину шага разности количественных показателей экспертной оценки исследуемых объектов между смежными ячейками таблицы.
Например, эксперты оценивали эффективность работы 10-ти лечебно-профилактических учреждений (ЛПУ1-10). По «Шкале количественной оценки выраженности признака (явления) у сравниваемых объектов (баллы)», эксперты оценили самое эффективное учреждение на 8 баллов (очень высокое), а наименее эффективное на 6 (выше среднего) баллов. Разность этих показателей составляет 2 балла. Два деленное на 8 (так как из девяти ячеек таблицы первая и последняя будут содержать максимальный и минимальный баллы соответственно) составит 0,25 (частное округляем до сотых). Если при заполнении таблицы по результатам сопоставительной оценки ЛПУ экспертами, в 3-ью позицию I-ой группы были отнесены два учреждения – ЛПУ3 и ЛПУ5, в 3-ью позицию III-ей группы также были отнесены два учреждения – ЛПУ2 и ЛПУ6, а во 2-ую позицию II группы не вошло по мнению экспертов ни одно из оцениваемых ЛПУ (см. табл. 2), в таком случае таблица будет иметь вид.
Таблица 2
Количественно-качественная сопоставительная экспертная оценка объектов по уровню выраженности у них проявления исследуемого признака (явления)
|
Позиции в группе |
Группы |
||
|
I |
II |
III |
|
|
1 Максимальное проявление признака в данной группе |
ЛПУ4 8,00 |
ЛПУ1 7,50-0,25 = 7,25 |
ЛПУ7 6,75-0,25 = 6,50 |
|
2 среднее проявление признака в данной группе |
ЛПУ9 8,00-0,25 = 7,75 |
7,25-0,25 = 7,00 |
ЛПУ8 6,50-0,25 = 6,25 |
|
3 Ниже среднего проявление признака в данной группе |
ЛПУ3; ЛПУ5 7,75-0,25 = 7,50 |
ЛПУ10 7,00-0,25 = 6,75 |
ЛПУ2; ЛПУ6 6,00 |
Из представленных в табл. 2 данных, видно, что получены количественные сопоставительные оценки эффективности работы ЛПУ, представляющие собой комплексный показатель эффективности деятельности каждого из них на основе применения интервальной шкалы.
Таким образом, полученные с использованием данной модели и технологии показатели могут применяться в качестве внешнего критерия, предоставляют возможность использования средней арифметической величины, допустимых для показателей интервальной шкалы методов математико-статистической обработки, а также позволяют ранжировать исследуемые объекты по уровню выраженности у них проявления исследуемого признака (явления) на основе экспертных оценок. Разработанная модель экспертной количественной сопоставительной оценки объектов (явлений) представляется удобной, понятной для работы экспертов и информативной по содержанию полученных с ее применением показателей.

