Комплексная предпосевная обработка семенного материала предполагает проведение ряда технологических процессов одновременно [3, 9]. Эффективность данной обработки во многом будет обусловлена направленным движением частиц обрабатываемого материала, поэтому важно представлять возможное влияние конструктивно-технологических параметров усовершенствованных классификаторов [2, 5, 6, 11] на траектории проходовых и непроходовых частиц [12, 13, 14]. Под проходовыми понимаем те частицы, которые просеиваются сквозь отверстия решет во время движения рабочего органа. Основываясь только на аналитических исследованиях, трудно количественно оценить реальные возможные соотношения изменений одних параметров от других.
Цель исследований: проведение вычислительного эксперимента с рассмотрением движения частиц по верхнему и среднему большему решетам, в виду того, что данные решета по размерам являются наибольшими и определяют габариты классификатора в целом и движение частиц обрабатываемого материала начинается именно здесь. Важность расчетов предельных траекторий заключается также в том, что необходимо иметь четкие представления о возможном влиянии размеров рабочих органов на эффективность проводимых технологических процессов, а именно: импакции и обработки физическими факторами [7, 8, 10].
Материалы и методы исследования
Максимально возможная траектория проходовой частицы при отклонении рабочего органа классификатора влево складывается (рис.1а) из траектории в горизонтальной плоскости hгор по проходовому решету плюс величина падения hпп плюс величина перемещения крайней левой точки соответствующего решета плюс величина траектории по непроходовому решету hгорп плюс величина взлета hвп, определяемая по [4].
Максимально возможная траектория проходовой частицы при отклонении рабочего органа классификатора вправо складывается (рис. 1б) из траектории в горизонтальной плоскости hгор по проходовому решету плюс величина падения hпн плюс траектории в горизонтальной плоскости после просеивания hгорп плюс величина перемещения крайней правой точки соответствующего решета плюс величина взлета hвн .
Максимально возможные траектории проходовой частицы при обработке на конусном классификаторе [2] при отклонении влево (рис. 1а) с горизонтальным элементом в верхнем положении равны:
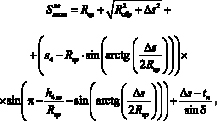 (1)
(1)
где Rвр – радиус верхнего решета, м; Rсбр – диаметр среднего большего решета, м; Δs – расстояние между решетами, м; s4 – расстояние от основания каркаса до верхнего решета, точка понижения, м; h4лв – положение крайней правой точки верхнего решета при отклонении влево, точка повышения, м; tп – толщина проходовой частицы, м [1].
Максимально возможные траектории проходовой частицы при обработке на магнитном [9] или пирамидальном классификаторе [4] при отклонении влево соответственно равны половине диагонали конкретного решета Врм или Врп плюс высота падения hпМ или hпП плюс соответствующая величина перемещения крайней левой точки АаМ или АаП плюс высота взлета:
 ; (2)
; (2)
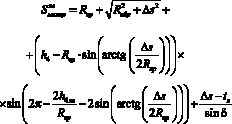 . (3)
. (3)
Максимально возможные траектории проходовой частицы при обработке на конусном классификаторе при отклонении вправо (рис. 1б) с горизонтальным элементом в верхнем положении равны:
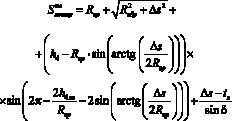 , (4)
, (4)
где h4 – расстояние от основания каркаса до верхнего решета, точка повышения, м.
Максимально возможные траектории проходовой частицы при обработке на магнитном или пирамидальном классификаторе при отклонении вправо соответственно равны половине диагонали конкретного решета ВрМ или ВрП, плюс высота падения hпМ или hпП, плюс соответствующая величина перемещения крайней правой точки ВаМ или ВаП, плюс высота взлета:
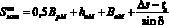 ; (5)
; (5)
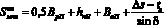 . (6)
. (6)
Вычислительный эксперимент проводили по уравнениям (1, 4) с учетом [1, 12, 13]. В расчетах использовали следующие значения входящих в формулы (1), (4) параметров: Rвр = [0,3; 0,35; 0,4; 0,45; 0,5] м; Rсбр = [0,18; 0,25; 0,33; 0,38; 0,4] м при Δs = [0,1; 0,15; 0,2] м; δ = 60 град. Значения параметров h4, h4лв, s4 определяли с учетом величин радиусов решет по зависимостям [4].
Результаты исследования и их обсуждение
По результатам полученных значений были построены поверхности отклика в среде Excel (рис. 2–4).
Анализируя полученные числовые значения максимально возможных траекторий проходовой частицы, выявлена существенная взаимосвязь. Изменяя соотношения размеров решет и расстояния между ними, мы получаем не пропорциональную зависимость варьирования величин траекторий.
В некоторых случаях мы получает превышение значения траектории при движении влево, а в некоторых при движении вправо. Это важно учитывать при дальнейшем изготовлении классификаторов, так как все эти возможные изменения будут оказывать существенное влияние на эффективность всей комплексной предпосевной обработки.
При соотношении решет 1,7 (0,3/0,18 м) и увеличении расстояния между ними с 0,1 м на 0,05 м предельная траектория движения влево проходовой частицы увеличивается на 13,7 % (рис. 2а, 3а), а вправо – увеличивается на 13,3 % (рис. 2б, 3б); при дальнейшем увеличении расстояния между решетами еще на 0,05 м траектория влево увеличивается на 13,2 % (рис. 3а, 4а); вправо – увеличивается на 12,7 % (рис. 3б, 4б); при изменении расстояния между решетами на 0,1 м предельная траектория движения влево проходовой частицы увеличивается на 28,7 % (рис. 2а, 4а), а вправо – увеличивается на 27,9 % (рис. 2б, 4б).
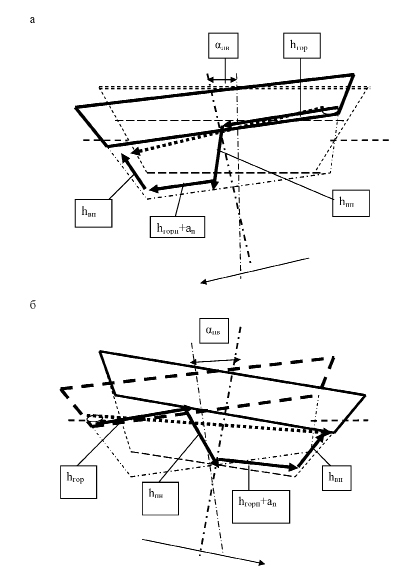
Рис. 1. Расчетная схема траекторий проходовых частиц: а – движение влево; б – движение вправо
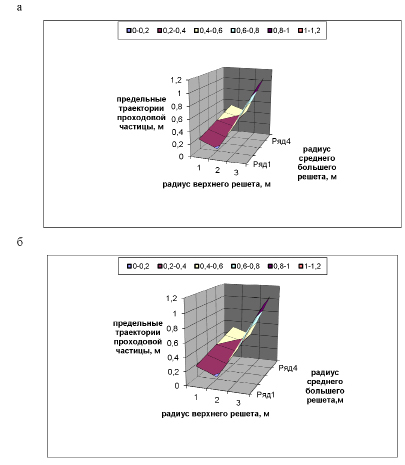
Рис. 2. Предельные траектории проходовой частицы при расстоянии между решетами 0,1 м: а – движение влево; б – движение вправо
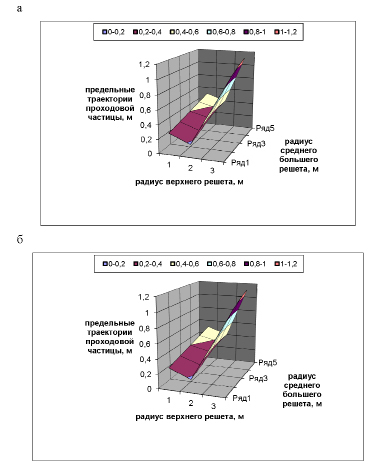
Рис. 3. Предельные траектории проходовой частицы при расстоянии между решетами 0,15 м: а – движение влево; б – движение вправо
При соотношении решет 1,4 (0,35/0,25 м) и увеличении расстояния между ними с 0,1 м на 0,05 м предельная траектория движения влево проходовой частицы увеличивается на 10,7 % (рис. 2а, 3а), а вправо – увеличивается на 10,6 % (рис. 2б, 3б); при дальнейшем увеличении расстояния между решетами еще на 0,05 м траектория влево увеличивается на 10,8 % (рис. 3а, 4а); вправо – увеличивается на 10,5 % (рис. 3б, 4б); при изменении расстояния между ними на 0,1 м предельная траектория движения влево проходовой частицы увеличивается на 22,7 % (рис. 2а, 4а), а вправо – увеличивается на 22,1 % (рис. 2б, 4б).
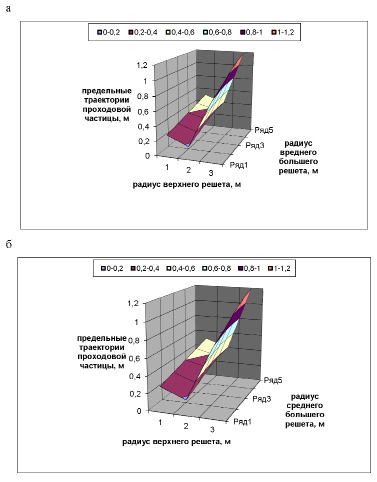
Рис. 4. Предельные траектории проходовой частицы при расстоянии между решетами 0,2 м: а – движение влево; б – движение вправо
При соотношении решет 1,2 (0,4/0,33 м) и увеличении расстояния между ними с 0,1 м на 0,05 м предельная траектория движения влево проходовой частицы увеличивается на 8,7 % (рис. 2а, 3а), а вправо – увеличивается на 8,6 % (рис. 2б, 3б); при дальнейшем увеличении расстояния между решетами еще на 0,05 м траектория влево увеличивается на 9,1 % (рис. 3а, 4а); вправо – увеличивается на 8,4 % (рис. 3б, 4б); при изменении расстояния между ними на 0,1 м предельная траектория движения влево проходовой частицы увеличивается на 18,6 % (рис. 2а, 4а), а вправо – увеличивается на 17,7 % (рис. 2б, 4б).
При соотношении решет 1,18 (0,45/0,38 м) и увеличении расстояния между ними с 0,1 м на 0,05 м предельная траектория движения влево проходовой частицы увеличивается на 7,7 % (рис. 2а, 3а), а вправо – увеличивается на 8,5 % (рис. 2б, 3б); при дальнейшем увеличении расстояния между решетами еще на 0,05 м траектория влево увеличивается на 8,5 % (рис. 3а, 4а); вправо – увеличивается на 7,7 % (рис. 3б, 4б); при изменении расстояния между ними на 0,1 м предельная траектория движения влево проходовой частицы увеличивается на 16,9 % (рис. 2а, 4а), а вправо – увеличивается на 15,8 % (рис. 2б, 4б).
При соотношении решет 1,25 (0,5/0,4 м) и увеличении расстояния между ними с 0,1 м на 0,05 м предельная траектория движения влево проходовой частицы увеличивается на 7,3 % (рис. 2а, 3а), а вправо – увеличивается на 7,0 % (рис. 2б, 3б); при дальнейшем увеличении расстояния между решетами еще на 0,05 м траектория влево увеличивается на 8,5 % (рис. 3а, 4а); вправо – увеличивается на 7,4 % (рис. 3б, 4б); при изменении расстояния между ними на 0,1 м предельная траектория движения влево проходовой частицы увеличивается на 16,5 % (рис. 2а, 4а), а вправо – увеличивается на 14,9 % (рис. 2б, 4б).
При варьировании соотношения радиусов решет по ряду 1,7; 1,4; 1,2; 1,18; 1,25 разница изменений предельных траекторий составляет, соответственно, при увеличении расстояния между решетами на 0,05 м (с 0,1 м до 0,15 м): 0,4 %; 0,1 %; 0,1 %; –0,8 %; 0,3 %; при увеличении расстояния между решетами еще на 0,05 м (с 0,15 м до 0,2 м) на: 0,5 %; 0,3 %; 0,6 %; 0,8 %; 1,1 %; при увеличении расстояния между решетами сразу на 0,1 м (с 0,1 м до 0,2 м): 0,8 %; 0,6 %; 0,9 %; 1,1 %; 1,6 %. Знак «-» означает более интенсивное изменение при движении вправо.
Все это объясняется видом траектории движения частиц – в виде знака бесконечности [4, 5], а также взаимодействием частиц между собой – пространственной переориентацией [3]. Общие результаты вычислительного эксперимента полностью подтверждают правильность и адекватность всех наших теоретических исследований.
Выводы
1. Полученные числовые величины и соотношения свидетельствуют о возможности влияния на процесс комплексной предпосевной обработки семенного материала за счет изменения конструктивно-технологических параметров классификаторов, прогнозируя тем самым эффективность реализации этой обработки.
2. В результате вычислительного эксперимента была выявлена не пропорциональная зависимость варьирования величин траекторий от соотношения величин решет и расстояния между ними.
3. Меняя соотношения размеров решет от 1,2 до 1,7, можно получить изменение предельных траекторий проходовых частиц на 7,0 % – 28,7 %.
4. Результаты вычислительного эксперимента полностью подтверждают правильность и адекватность проведенных теоретических исследований в области создания новой технологии предпосевной обработки семенного материала и технических средств, ее реализующих.
5. Полученные числовые соотношения будут использованы при изготовлении классификаторов.

