Рассмотрим стержень ограниченной длины L, см, площадь поперечного сечения которого F, см2, постоянна по ее длине. Стержень изготовлен из жаропрочного сплава АНВ-300. Значение коэффициента теплового расширение этого материала α, 1/ºC, строго зависит от значения температуры, т.е. 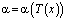 . Здесь
. Здесь 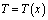 – поле распределения температуры по длине стержня, которое необходимо определить с учетом существующих граничных условий. Коэффициент теплопроводности материала стержня обозначим через Kxx, Вт/(см•ºC), а модуль упругости через Е, кГ/см2. Расчетная схема рассматриваемой задачи приводится на рис. 1.
– поле распределения температуры по длине стержня, которое необходимо определить с учетом существующих граничных условий. Коэффициент теплопроводности материала стержня обозначим через Kxx, Вт/(см•ºC), а модуль упругости через Е, кГ/см2. Расчетная схема рассматриваемой задачи приводится на рис. 1.
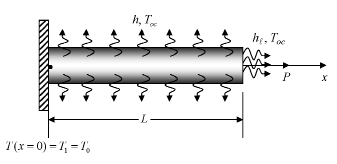
Рис. 1. Расчетная схема рассматриваемой задачи
Предположим, что левый конец стержня жестко-защемлен и совпадает с началом координат. На этом конце задана температура 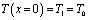 . Через площади боковой поверхности и поперечного сечения правого конца происходит теплообмен с окружающей средой. При этом температура окружающей среды Тос, ºC, коэффициент теплообмена h, Вт/(см•ºC) и ее значение также постоянна во всюду. Кроме того, на правом конце стержня приложена осевая растягивающая сила P, кГ. Требуется определить поле распределения температуры
. Через площади боковой поверхности и поперечного сечения правого конца происходит теплообмен с окружающей средой. При этом температура окружающей среды Тос, ºC, коэффициент теплообмена h, Вт/(см•ºC) и ее значение также постоянна во всюду. Кроме того, на правом конце стержня приложена осевая растягивающая сила P, кГ. Требуется определить поле распределения температуры 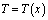 по длине стержня с учетом наличия источника тепла и глобального теплообмена. Также необходимо вычислить удлинение стержня от теплового расширения и растягивающей силы Р.
по длине стержня с учетом наличия источника тепла и глобального теплообмена. Также необходимо вычислить удлинение стержня от теплового расширения и растягивающей силы Р.
Для этого сначала дискретизируем рассматриваемый стержень n элементами одинаковой длины. Каждый элемент рассмотрим как квадратный конечный элемент с тремя узлами. Тогда число всех узлов будет равно ЧУЗ=2n+1. Далее для каждого элемента напишем выражение функционала, которое характеризует полную тепловую энергию с учетом имеющихся граничных условий. В частности, для первого элемента такой функционал имеет следующий вид [1–3]:
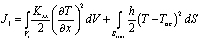 , (1)
, (1)
где V1 – объем первого элемента; S1пбп – площадь боковой поверхности первого элемента. С учетом (3) для первого элемента имеем, что
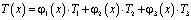 ,
, 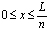 ; (2)
; (2)
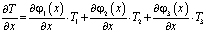 ,
, 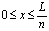 ; (3)
; (3)
где T1, T2 и T3 – значения температур в узлах первого элемента. При этом
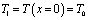 ;
; 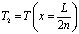 ;
; 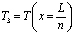 . (4)
. (4)
Будем учитывать, что
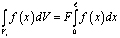 ,
,
где F – площадь поперечного сечения рассматриваемого элемента стержня; 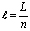 – длина элемента стержня;
– длина элемента стержня;
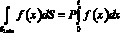 ,
,
где P – периметр поперечного сечения, а также интеграла по площади поперечного сечения
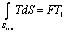 .
.
Тогда для первого элемента интегрированный вид функционала (1) имеет следующий вид:
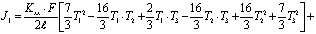
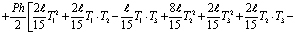
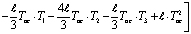 . (5)
. (5)
Начиная со второго до (n–1)-го элемента выражение соответствующего функционала для каждого элемента имеет следующий интегрированный вид
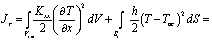
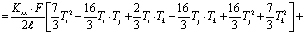
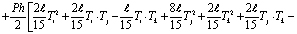
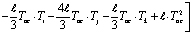 ,
, 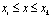 , (6)
, (6)
где 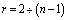 – номер элемента;
– номер элемента; 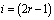 ;
; 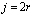 ;
; 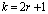 и
и
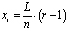 ;
; 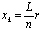 .
.
Наконец, для последнего n-го элемента выражение функционала, которое характеризует полную тепловую энергию имеет следующий интегрированный вид
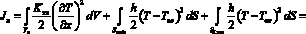
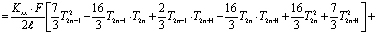
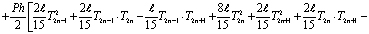
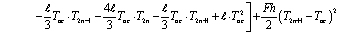 , (7)
, (7)
где 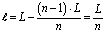 ; SLппc – площадь поперечного сечения правого конца стержня.
; SLппc – площадь поперечного сечения правого конца стержня.
Тогда выражение функционала, которое характеризует полную тепловую энергию рассматриваемого стержня, в целом имеет следующий вид
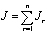 , (8)
, (8)
Учитывая, что значение температуры в первом узле задано, т.е. 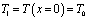 , минимизируя функционал (8) по узловым значениям температуры
, минимизируя функционал (8) по узловым значениям температуры 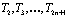 построим следующую разрешающую систему линейных алгебраических уравнений
построим следующую разрешающую систему линейных алгебраических уравнений
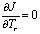 ,
, 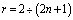 . (9)
. (9)
Решая последнею систему, находим значения температур в узлах элементов. Пользуясь соотношением (3), находим закон распределения поля температур в пределах каждого элемента, а по ним по длине рассматриваемого стержня в целом.
В работе [4] для жаропрочного тугоплавкого сплава приводится результаты натурного эксперимента по определению зависимости коэффициента теплового расширения от температуры в виде графиков. Эти данные в первом разделе приведены в табличной форме, в том числе и для сплава АНВ-300.
Из результатов натурного эксперимента работы [4] видно, что 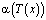 меняется линейно в интервале температур
меняется линейно в интервале температур
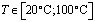 ;
; 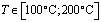 ;
; 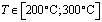 ;
;
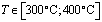 ;
; 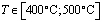 ;
; 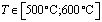 ;
;
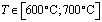 ;
; 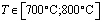 .
.
Поэтому эти зависимости можно описать математически следующим образом
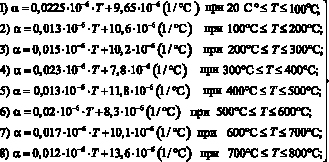 (10)
(10)
Кроме того, известно (раздел 1), что поле распределение коэффициента теплового расширения для r-го элемента определяется (1.35), где 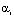 ,
, 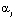 и
и 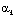 – узловые значения коэффициента теплового расширения в r-м элементе;
– узловые значения коэффициента теплового расширения в r-м элементе; 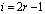 ;
; 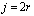 ;
; 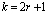 .
.
Тогда узловые значения α определяются исходя из закона распределения температуры в каждом элементе и с помощью соотношения (10). А величина удлинение r-того элемента определяется с помощью соотношения
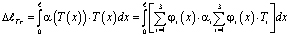 , (11)
, (11)
где 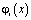 – функция формы для r-го квадратичного элемента;
– функция формы для r-го квадратичного элемента; 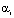 , Ti – узловые значения коэффициента теплового расширения и температуры r-го квадратичного элемента.
, Ti – узловые значения коэффициента теплового расширения и температуры r-го квадратичного элемента.
Тогда общее удлинение рассматриваемого стержня в целом от теплового расширения определяется следующим образом
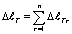 . (12)
. (12)
На основе закона Гука удлинение рассматриваемого стержня от осевой растягивающей силы Р определяется следующим образом
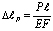 . (13)
. (13)
Тогда величина общего удлинения рассматриваемого стержня будет
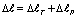 . (14)
. (14)
Для реализации вышеизложенного алгоритма примем за исходные данные следующее
Kxx=72 Вт/(см2•ºС); h=10 Вт/(см2•ºС);
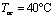 ;
;
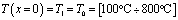 ;
;
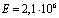 кГ/см2;
кГ/см2; 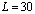 см;
см; 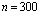 ;
;
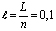 см.
см.
Форма поперечного сечения рассматриваемого стержня является круг радиусом 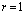 см. Площадь поперечного сечения
см. Площадь поперечного сечения 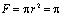 (см2), а периметр
(см2), а периметр 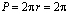 (см).
(см).
На рис. 2 приводится поле распределения температур по длине стержня при разных значениях T0, а в таблице приводятся значения 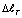 при разных значениях T0, т.е. зависимость между T0 и
при разных значениях T0, т.е. зависимость между T0 и 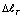 , R,
, R, 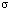 . Из рис. 2 видно, что поле распределения температуры по длине стержня будет гладкой кривой. Графическая зависимость между величинами источника температуры T0 и соответствующего удлинение стержня
. Из рис. 2 видно, что поле распределения температуры по длине стержня будет гладкой кривой. Графическая зависимость между величинами источника температуры T0 и соответствующего удлинение стержня 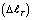 от теплового расширения приводится на рис. 3.
от теплового расширения приводится на рис. 3.
При T0 =100ºС, начиная с x=15,5 см, т.е. на участке 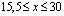 см наблюдается постоянная температура, значения, которого равна
см наблюдается постоянная температура, значения, которого равна 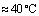 . В этом случае из за теплового расширения стержень удлиняется на
. В этом случае из за теплового расширения стержень удлиняется на 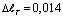 см. Для сравнения, следует сказать, что это удлинение эквивалентно к удлинению стержня, если его растягивать силой
см. Для сравнения, следует сказать, что это удлинение эквивалентно к удлинению стержня, если его растягивать силой 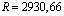 кГ. Естественно, на основе закона Гука в этом случае в сечении стержня возникало бы растягивающее напряжение величиной
кГ. Естественно, на основе закона Гука в этом случае в сечении стержня возникало бы растягивающее напряжение величиной 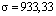 кГ/см2.
кГ/см2.
При увеличении значения заданной температуры в два раза, т.е. при 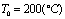 на участке
на участке 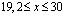 , см, наблюдается 40°С поле температуры. В этом случае величина удлинение стержня составляет
, см, наблюдается 40°С поле температуры. В этом случае величина удлинение стержня составляет 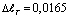 см и будет больше на 17,657 % чем в случае T0 =100ºС. Эта величина удлинение эквивалентно к удлинению стержня находящейся по растягивающей нагрузкой R=3454 кГ. При этом растягивающее напряжение было бы =1100 кГ/см2. Если увеличить значение точечной температуры в три раза, т.е. при T0 =300ºС величина
см и будет больше на 17,657 % чем в случае T0 =100ºС. Эта величина удлинение эквивалентно к удлинению стержня находящейся по растягивающей нагрузкой R=3454 кГ. При этом растягивающее напряжение было бы =1100 кГ/см2. Если увеличить значение точечной температуры в три раза, т.е. при T0 =300ºС величина 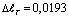 см, что превышает на 37,857 % чем в случае T0 =100ºС. Также следует отметить, что в этом случае на участке
см, что превышает на 37,857 % чем в случае T0 =100ºС. Также следует отметить, что в этом случае на участке 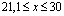 см стержня наблюдается постоянная температура близко к температуре окружающей стержня среды. В этом случае величина
см стержня наблюдается постоянная температура близко к температуре окружающей стержня среды. В этом случае величина 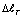 эквивалентно к растяжению рассматриваемого стержня с силой R=4040 кГ. При этом значение растягивающего напряжения возникающих в сечениях составляло бы =1286 (кГ/см2). Следует отметить, что для обычных сталей это напряжение уже превышает предел пропорциональности.
эквивалентно к растяжению рассматриваемого стержня с силой R=4040 кГ. При этом значение растягивающего напряжения возникающих в сечениях составляло бы =1286 (кГ/см2). Следует отметить, что для обычных сталей это напряжение уже превышает предел пропорциональности.
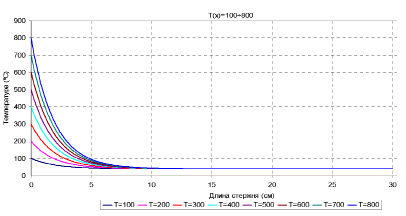
Рис. 2. Поле распределение температуры по длине стержня при разных значениях T0
Зависимость между T0 и 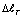 , R, σ
, R, σ
|
№ п/п |
|
|
Эквивалентная «растягивающая» сила R, кГ, при котором получилось бы такое удлинение |
Эквивалентное «растягивающее напряжение» σ, кГ/см2 |
|
Относи-тельное удлинение, % |
раз |
|
1. |
100 |
0,014 |
2930,66 |
933,33 |
0,0133 |
0,047 |
1,052 |
|
2. |
200 |
0,0165 |
3454 |
1100 |
0,0152 |
0,055 |
1,085 |
|
3. |
300 |
0,0193 |
4040,1 |
1286,66 |
0,0171 |
0,064 |
1,129 |
|
4. |
400 |
0,02247 |
4703,72 |
1498 |
0,0190 |
0,075 |
1,183 |
|
5. |
500 |
0,0259 |
5432,2 |
1730 |
0,0209 |
0,086 |
1,239 |
|
6. |
600 |
0,0297 |
6217,2 |
1980 |
0,0228 |
0,1 |
1,303 |
|
7. |
700 |
0,03388 |
7092,2 |
2258,66 |
0,0247 |
0,113 |
1,372 |
|
8. |
800 |
0,038 |
7954,66 |
2533,33 |
0,0267 |
0,127 |
1,423 |
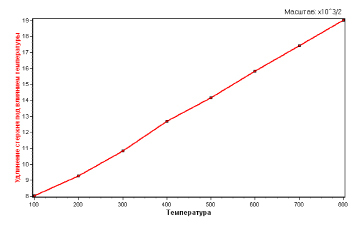
Рис. 3. Графическая зависимость между T0 и 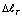
Теперь увеличивая значение T0 в четыре раза, т.е. при T0 =400 °C имеем, что 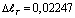 см. Это эквивалентно к удлинению стержня при ее растяжении силой, величина которого R=4703,72 кГ. В этом случае в сечениях стержня возникало бы растягивающее напряжение величиной ?=1498 (кГ/см2). Естественно для обычных сталей это напряжение считается разрушающей. При T0 =500°C значение
см. Это эквивалентно к удлинению стержня при ее растяжении силой, величина которого R=4703,72 кГ. В этом случае в сечениях стержня возникало бы растягивающее напряжение величиной ?=1498 (кГ/см2). Естественно для обычных сталей это напряжение считается разрушающей. При T0 =500°C значение 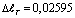 см. Это на 85 % больше чем аналогичное значение
см. Это на 85 % больше чем аналогичное значение 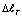 при T0 =100°C. Здесь следует отметить, для того чтобы получить удлинение стержня в размере
при T0 =100°C. Здесь следует отметить, для того чтобы получить удлинение стержня в размере 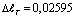 см при ее растяжении необходимо было бы растянуть с силой R=5432,1 кГ. При этом в сечениях стержня появилось бы растягивающее напряжение =1730 (кГ/см2), которое является большим для обычных стальных конструкции. Необходимо отметить, что при T0 =600°C величина
см при ее растяжении необходимо было бы растянуть с силой R=5432,1 кГ. При этом в сечениях стержня появилось бы растягивающее напряжение =1730 (кГ/см2), которое является большим для обычных стальных конструкции. Необходимо отметить, что при T0 =600°C величина 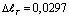 см и она будет на 112,14 % больше чем
см и она будет на 112,14 % больше чем 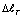 при T0 =100°C. Эквивалентная растягивающая сила было бы равно R=6217,2 кГ и соответствующее растягивающее напряжение будет равно =1980 кГ/см2. Интересно отметить, что при увеличение значение температуры T0 от T0 =100°C до T0 =600°C, значения
при T0 =100°C. Эквивалентная растягивающая сила было бы равно R=6217,2 кГ и соответствующее растягивающее напряжение будет равно =1980 кГ/см2. Интересно отметить, что при увеличение значение температуры T0 от T0 =100°C до T0 =600°C, значения 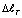 , R и σ увеличиваются одинаково на 112,14 %.
, R и σ увеличиваются одинаково на 112,14 %.


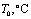
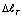 , см
, см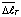 , см, при
, см, при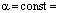
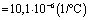
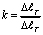 ,
,