Расчет сетчатых и подкрепленных оболочек как систем, имеющих сложную структуру, вызывает вычислительные и принципиальные трудности. Их разрешение на основе уточнения классической теории оболочек с применением новых модельных представлений и подходов, совершенствования методов и методик расчета является одной из самых актуальных проблем механики оболочечных конструкций и представляет несомненный практический интерес.
Рассмотрим круговую сетчатую цилиндрическую оболочку бесконечной длины, закрытую непроникаемой плёнкой и обтекаемую сверхзвуковым потоком газа с невозмущённой скоростью u, направленной вдоль образующих оболочек, т.е. по координатом a (рис. 1).
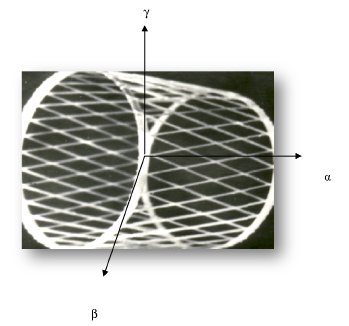
Рис. 1. Цилиндрическая сетчатая оболочка из КМ
Предполагая, что давленение газа Р на обтекаемую поверхность оболочки через плёнку может быть вычислено при помощи приближённой формулы поршневой теории [1]
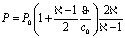, (1)
где P0 – давление невозмущённого потока газа;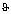 
– нормальная составляющая скорости потока газа, обтекающего поверхность оболочки; с0 – скорость звука в невозмущенном газе; 
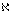– показатель политропы.
Следуя работам [2,3], будем считать, что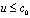 
и, разложив уравнение (1) в ряд по формуле бином Ньютона для малых возмущений, в первом приближении c учетом
,
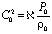будем иметь:
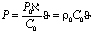. (2)
Рассмотрим линеаризованное течение газа вдоль оболочки, по которой распространяются упругие волны. В этом случае:
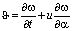(3)
и следовательно, по формуле избыточного давления
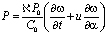(4)
Кроме того, примем во внимание линейное демпфирование ε.
Тогда получим следующие динамические уравнения для цилиндрической сетчатой оболочки, обтекаемой сверхзвуковым потоком газа а направлении α.
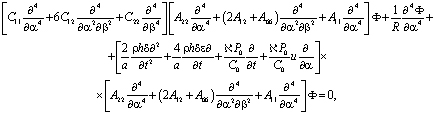(5)
где a – расстояние между осями стержней, и согласно [4] принимаем:
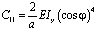
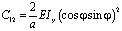(6)
;
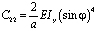
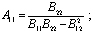
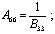
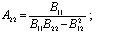
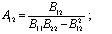
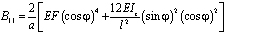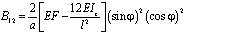; (7)
.
.
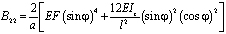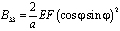Решение уравнения (5) ищем в виде волн, распространяющихся по поверхности оболочки:
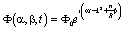, (8)
где Ф0 – некоторая комплексная постоянная; 
– частота колебаний оболочки: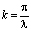 
– волновое число;