Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Представим энергетическую модель агрегата в виде энергетических составляющих, количество которых определяется назначением агрегата:

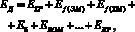
где EД – энергия, развиваемая двигателем энергетического модуля; EТР – затраты энергии на преодоление сопротивлений в трансмиссии и движителе; 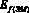– энергия, необходимая для самопередвижения энергетического модуля; 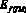– затраты энергии на перекатывание рабочей машины; 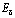– энергия, затрачиваемая на буксование; EВОМ – затраты энергии на привод рабочих органов от ВОМ; EКР – затраты энергии на протаскивание рабочих органов.

Рассматривая технологический модуль как совокупность технологических операций, выполняемых определенным набором агрегатов для решения задачи оптимизации энергозатрат используем модель закрытой распределительной задачи линейного программирования [5]. Система уравнений (1) представляет собой удельные затраты энергии по агрегатам (Ai), , система уравнений (2), соответственно, затраты энергии по составляющим энергетической модели агрегатов (затраты энергии на самопередвижение, т.д. (Мi).

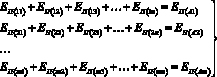(1)

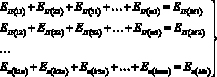(2)

Формализуем модель в общепринятую систему, для этого представим системы (1) и (2) следующим образом:

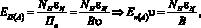
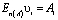; (3)

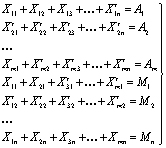(4)

где .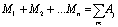

Задача оптимизации энергозатрат сводится к отысканию решения при минимизации линейной функции

y = C11X11+C12X12+…СminXmin >min.

При этом, за критерий оптимизации принимаем минимальный погектарный расход топлива агрегатами: Gга(Аi) >min.

Переменные Хij представляют собой удельные затраты мощности на единицу ширины захвата рабочей машины, Вт/м (в трансмиссии, приводе рабочих органов от ВОМ., и т.д.) для определённой удельной производительности агрегатов (м2/Дж.)[1] по видам работ. Коэффициенты Сij – соответственно, доли удельного расхода топлива на единицу скорости. Решение задачи сводится к определению исходного опорного решения и последовательному выполнению итераций по приближению к оптимальному решению.

Элементарный подход к решению системы уравнений невозможен, так как, наряду с неизвестными Хij, не определены и Aij, Mij, Cij. Поэтому на первом этапе решения поставленной задачи формализуем эти показатели. Для определения Ai воспользуемся нормативными требованиями на затраты энергии для выполнения определенной технологической операции, рассчитываемыми на перспективные технологии. Тогда энергетическая составляющая на преодоление механических потерь в трансмиссии и движителе определяется из условия:

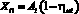
и 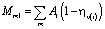, (5)

где ηм(i) – механический к.п.д.

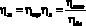. (6)

Энергетическая составляющая на самопередвижение энергосредства:

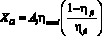. (7)

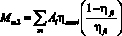. (8)

Энергетическая составляющая, затрачиваемая на буксование:

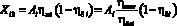. (9)

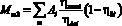(10)

Энергетическую составляющую на протаскивание технологического модуля делим на две составляющие:

а) затраты энергии на преодоление сопротивления качению технологического модуля;

б) затраты энергии на преодоление сопротивления рабочих органов технологического модуля

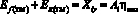. (11)

где тяговый к.п.д. определяется, соответственно, для тягового и тягово-приводного агрегатов:

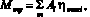(12)

Энергетическая составляющая на привод от ВОМ:

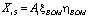. (13)

где 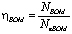. (14)

Тогда затраты энергии на контрпривод для выполнения технологического процесса:

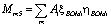. (15)

При переводе ТМ в движитель:

. (16)

Если от ВОМ совместный привод на движитель и на рабочие органы (контрпривод)

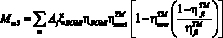. (17)

где 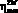, 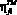– тяговый к.п.д. и к.п.д. сопротивления движению технологического модуля с движителем.

С правомерным допущением считаем, что затраты топлива прямо пропорциональны затратам энергии.

Если принять, что

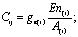
то 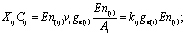и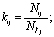

Тогда решение целевой функции примет вид

.

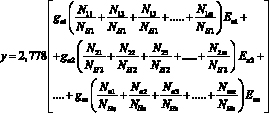Или

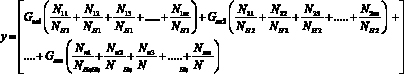(18)

То есть, в конечном итоге, задача сводится к оптимальному распределению мощности по составляющим энергетической модели агрегата, поиску конструктивно-режимных решений, снижающих непроизводительные затраты энергии (топлива)и максимальном ее использовании на выполнение полезной работы.

Умножим каждое уравнение системы (1) на выражение 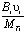, в итоге получим уравнения вида:

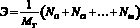. (19)

Представим удельные затраты мощности в виде

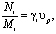
где ηi – удельный силовой параметр, Н/кг.

Тогда любое уравнение системы (1) примет вид

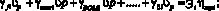(20)

Для прицепных агрегатов удельные затраты мощности на протаскивание технологического модуля:

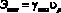; (21)

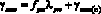, (22)

где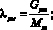

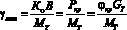. (23)

Для тягово-приводных агрегатов удельные затраты мощности на протаскивание рабочих органов:

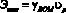
и 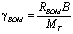. (24)

где RBOM – удельное тяговое сопротивление рабочих органов, приводимых от ВОМ, н/м.

Удельные потери мощности на буксование:

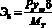(25)

Для полевых агрегатов удельная сила тяги представляет собой динамический фактор:

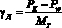. (26)

для малых скоростей ; и .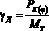

Тогда

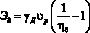. (27)

Но удельная сила тяги, развиваемая двигателем, реализуется движителем по условиям сцепления:

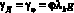. (28)

Для того чтобы определиться с направлениями повышения энергетической эффективности агрегатов за счет изменения конструктивно-режимных параметров, преобразуем систему (2) в матричную форму: принимая, что первая задача сводится к системе линейных уравнений в виде

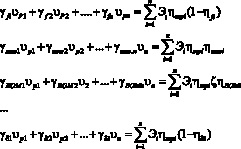(29)

Выразим удельный силовой параметр ηi через удельное тяговое сопротивление

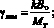
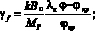
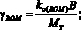
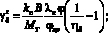
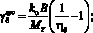(30)

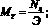Но и 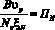– удельная чистая производительность при рабочем ходе агрегата, м2/Дж.

Тогда система (2) примет вид

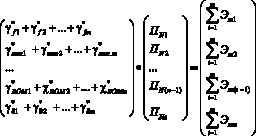. (31)

Или

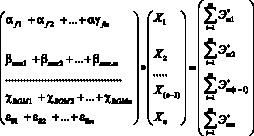, (32)

где

, , ;

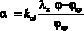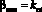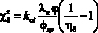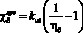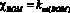
либо , , 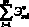на примере для

.

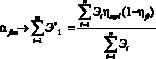Решение системы позволяет определить удельную чистую производительность агрегатов при меняющихся конструктивно-режимных параметрах, задаваемых через безразмерные измерители: коэффициент сцепления φ; коэффициент использования веса φкр; коэффициент сопротивления качению f; коэффициент нагрузки колес λк; буксование δи др.

Разработаные методические основы и математическая модель оценки энергетической эффективности агрегатов позволяют одновременно оценивать и оптимизировать энергетические затраты, как в агрегатах, так и в технологических процессах. Объектом и предметом полевых и хозяйственных испытаний служили: технологические процессы возделывания и уборку картофеля, тяговый агрегат на полугусеничном ходу; тягово-приводной агрегат с роторным плугом; комбинированный агрегат с фронтальным гидронавесным устройством; на базе трактора класса 1,4; самоходный гусеничный копатель-погрузчик, транспортно-технологический агрегат с центробежными дебалансами; транспортный агрегат с ведущим мостом модернизированного прицепа 2ПТС-6; на базе трактора класса 1,4.

Например установка на трактор МТЗ-80 полугусеничного хода, (увеличение коэффициента сцепления), позволила использовать его в агрегате с дисковой бороной БДТ-3. Т.е. установка полугусеничного хода на колесный трактор 1,4 позволяет использовать его на работах следующего тягового класса. (увеличение коэффициента использования веса), [4] .При этом удельные затраты энергии на единицу производительности при рабочем ходе агрегата составили 7,64 кДж/м2 (для агрегата ДТ-75–М+БДТ-3 – 7,79 кДж/м2).

Рис. 1. Трактор класса 1,4 с опцией полугусеничного хода

Для снижения составляющей тягового сопротивления разработан роторный плуг с активными сферическими дисками (ПРН-2,4) [2;3] . За счет снижения затрат энергии на рабочий процесс с 12,57 кДж/м2 до 6,23 кДж/м2 в целом удельные затраты энергии на единицу наработки на вспашке уменьшились с 19,7 кДж/м2 (агрегат ДТ-75М+ПЛН5–35) до 9,38 кДж/м2 (агрегат МТЗ-80 + ПРН-2,4) т.е. в 2,1 раза. При этом расход топлива уменьшился в 1,79 раза, производительность в час основного времени увеличилась в 1,33 раза, рабочая скорость – в 1,53 раза.

Рис. 2. Трактор в агрегате с роторным плугом

В целом применение новых конструктивно-технологических схем агрегатов снижающих непроизводительные затраты энергии в позволили значительно сократить энергоемкость выращивания картофеля.

Рис. 3. Комбинированный агрегат на обработке посадок картофеля

В результате к.п.д. движителя тяговых агрегатов вырос в 1,23 раза (с 0,61 до 0,75 ), транспортных агрегатов – в 1,15 раза (с 0,61 до 0,70), производительность на операциях по обработке почвы увеличилась в 1,13–1,33, на транспортных работах – в 1,06 –1,16 раза.

Энергоемкость технологических модулей базовой и усовершенствованной технологий выращивания картофеля, МДж/т

Таким образом, определив, от каких факторов зависит γi, можно влиять на составляющие энергетической модели агрегатов и, решая совместно систему уравнений 1 и 2, добиться максимального использования энергии на полезную работу в технологических процессах.