Современные вычислительные устройства имеют довольно сложную структуру. Увеличение обработки данных в реальном масштабе времени привело к использованию параллельной обработки. Параллельные вычисления широко применяются при цифровой обработке сигналов [6-8]. Применение параллельной обработки сигналов приводит к снижению надежности устройств, поэтому снижение отказов систем к сбоям является актуальной задачей. Данная задача наиболее эффективна за счет применения полиномиальной системы классов вычетов (ПСКВ) для обнаружения и коррекции ошибок при меньших временных затратах[3].
Цель исследования
Сохранение работоспособного состояния вычислительных устройств определяется быстротой и глубиной определения ошибок. Целью исследования является расширение функциональных возможностей устройства, то есть проведения коррекции ошибок кодом полиномиальной системы классов вычетов, на основе использования операций расширения оснований.
Материалы и методы исследования
Особенность ПСКВ заключается в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но также и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства [1-3]. В ПСКВ в качестве оснований системы используются неприводимые полиномы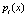 
, где 
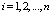, любой полином A(x), удовлетворяющий
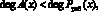(1)
где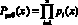 
– рабочий диапазон системы, 
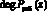– степень полинома, можно однозначно представить в виде набора остатков
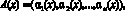(2)
где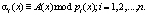 
Для обнаружения и исправления однократных ошибок в модулярном коде полинома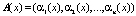 
вводят два контрольных основания 
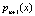и 
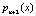, которые удовлетворяют условию
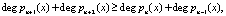(3)
Наличие двух контрольных основания позволяет определить местоположение ошибки и ее глубину в коде ПСКВ [4, 5, 8].
Возникновение ошибки в непозиционной кодовой конструкции A(z) переводит ее из подмножества разрешенных комбинаций в подмножество запрещенных. Согласно китайской теореме об остатках (КТО) значение ошибочного полинома A*(z) равно
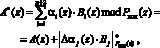(4)
где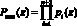 
– полный диапазон кода ПСКВ; 
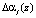– глубина ошибки по j-ому основанию кода ПСКВ; Bj(z) – ортогональный базис j-го основания ПСКВ; j = 1, 2, …, n + 2.
Анализ выражения (4) показывает, что местоположение ошибочного полинома A*(z) относительно рабочего диапазона Pраб(z) определяется величиной второго слагаемого.
Рассмотрим алгоритм перевода из безизбыточного полиномиального модулярного кода в позиционный код согласно КТО, имеем
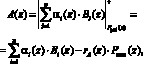(5)
где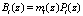 
– ортогональный базис; mi(z) – вес ортогонального базиса; 
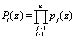; rA(z) – ранг кода ПСКВ.
Воспользуемся определением ортогональных базисов, тогда выражение (5) можно представить в виде
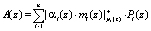(6)
Умножение остатка на вес ортогонального базиса выполняется по модулю pi(z), что позволяют отказаться от вычисления ранга rA(z) при использовании китайской теоремы об остатках при переводе к позиционному коду.
Чтобы осуществить поиск и коррекцию ошибки в коде ПСКВ на основе расширения системы оснований необходимо, используя остатки по рабочим основаниям (α1(z),…, αn(z)), вычислитель остатки по контрольным основаниям pn + 1(z) и pn + 2(z).
Тогда для вычисления первого контрольного остатка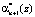 
по основанию 
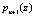используем следующее выражение
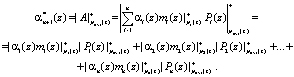(7)
Второй контрольный остаток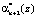 
по основанию 
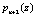определяется
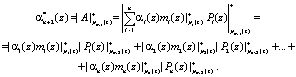(8)
После этого вычисленные остатк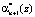и 
и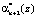 
складываются по модулю два с остатками 
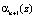и 
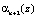, которые входят в состав комбинации кода ПСКВ 
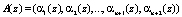. В результате получается синдром ошибки, который определит местоположение и глубину ошибки в коде
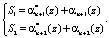(9)
Если полученный синдром будет равен нулю, то это означает, что код ПСКВ не содержит ошибки. Если синдром будет отличен от нуля, то это будет означать, что код ПСКВ содержит ошибку.
Результаты исследования и их обсуждение
Пусть задано поле Галуа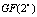 
, в котором определены информационные основания 
, 
, 
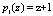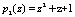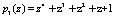, расширяем систему оснований за счет введения двух контрольных основани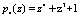й 
и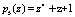 
. В этом случае
.
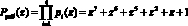При этом полный диапазон составляет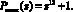 
Тогда контрольный полином
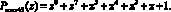
Определим значения рабочих основани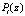й 
и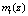 
:
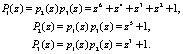
Тогда веса ортогональных базисов равны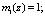 
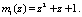
Следовательно, ортогональные базисы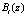 
соответственно равны
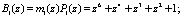
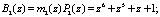
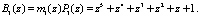
Воспользуемся полином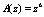 
, который представляется как 
.
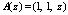Расширяем систему оснований за счет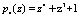 
и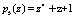 
. Первое основания расширения системы 
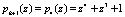. Вычислим значения 
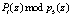. Тогда имеем
,
.
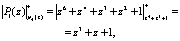
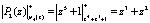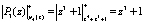Определим произведения
,
,
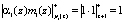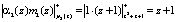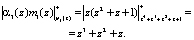
Подставляем полученные значения в выражение (7) и получаем
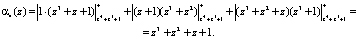
Результат расширения по основанию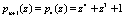 
получили остаток 
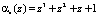. Проведем проверку и определим остаток исходного полинома
.
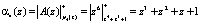Второе основание расширения
.
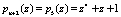Вычислим значения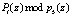 
. Тогда имеем
,
,
.
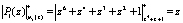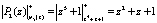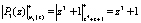Определим произведение
.
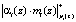Они соответственно равны
,
,
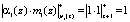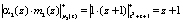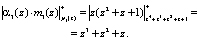
Подставляем полученные значения в выражение (8)
.
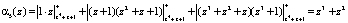Результат расширения по основанию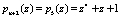 
– остаток 
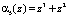. Проведем проверку и определим остаток исходного полинома
.
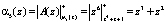Таким образом, расширенная комбинация избыточного кода ПСКВ будет иметь вид
.
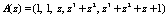Если на вход устройства и обнаружения ошибки, использующего разработанный алгоритм расширения системы оснований, поступит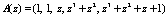 
, то синдром ошибки будет равен
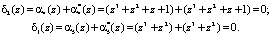
Так как синдром ошибки равен нулю, то код ПСКВ не содержит ошибки.
Рассмотрим ситуацию, когда проверяемая комбинация ПСКВ содержит ошибку по первому основанию и ее глубина равна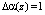 
. Тогда значение первого остатка равно 
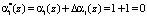. Ошибочная комбинация модулярного кода ПСКВ имеет вид
.
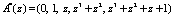Определим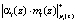 
, для данной ошибочной комбинации кода ПСКВ. Получаем
,
.
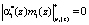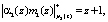
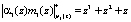Вычислим первый контрольный остаток, подставив значения в выражение (7)
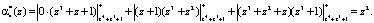
Результатом расширения по модулю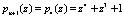 
является 
.
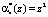Вычислим второй контрольный остаток, подставив значения в выражение (8)
.
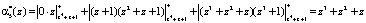Результатом расширения по модулю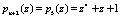 
является остаток 
.
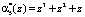Выполним проверку комбинации путем вычисления синдрома ошибки, имеем
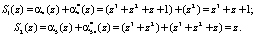
Проверяемая комбинация содержит ошибки, так как синдром ошибки отличен от нуля. В таблице приведены значения глубины и местоположения ошибки в коде ПСКВ по рабочим основаниям и соответствующего им синдрома ошибки S1(z) и S2(z). Данные в таблице приведены в шестнадцатеричной системе счисления. По значению синдрома ошибки определяем, что ошибка произошла по первому основанию p1(z) = z + 1, а ее глубина равна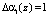 
. Значит, вектор ошибки будет равен 
.
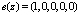Для коррекции ошибки необходимо данный вектор ошибки сложить с ошибочной комбинацией кода ПСКВ. Имеем
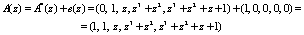
Глубина и местоположение ошибки в коде ПСКВ по S1(z) и S2(z)
|
Основание |
Глубина |
S1(z) |
S2(z) |
|
p1(z) = z + 1 |
1 |
B |
2 |
|
p2(z) = z2 + z + 1 |
1 |
7 |
9 |
|
2 |
A |
7 |
|
|
3 |
D |
E |
|
|
p3(z) = z4 + z3 + z2 + z + 1 |
1 |
E |
D |
|
2 |
1 |
F |
|
|
3 |
F |
2 |
|
|
4 |
6 |
B |
|
|
5 |
8 |
6 |
|
|
6 |
7 |
4 |
|
|
7 |
9 |
9 |
|
|
8 |
C |
5 |
|
|
9 |
2 |
8 |
|
|
A |
D |
A |
|
|
B |
3 |
7 |
|
|
C |
A |
E |
|
|
D |
4 |
3 |
|
|
E |
B |
1 |
|
|
F |
5 |
C |
Если ошибка произойдет по первому контрольному основанию p4(z) = z4 + z3 + 1, то значение первой составной синдрома S1(z) будет показывать глубину ошибки, а значение S2(z) будет равняться нулю.
Если ошибка произойдет по второму контрольному основанию p5(z) = z4 + z + 1, то значение второй составной синдрома S2(z) будет показывать глубину ошибки, а значение первой составляющей синдрома S1(z) будет равняться нулю.
Заключение
В статье проведено описание нового устройства коррекции ошибок в модулярном коде на основе расширения системы оснований. Представлены результаты применения данного устройства в кодах ПСКВ, за счет добавления двух контрольных оснований. Проведенные исследования показали, что при использовании двух контрольных оснований код ПСКВ исправляет все однократные ошибки при меньших схемных затратах.