Цель исследования
В статье установлена причинность явления превращения однородной жидкости в неоднородную в низкоразмерных системах, которая связана с величиной плотности воздействия проникающегося вглубь напряженности физического поля 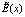 . Предложена физико-математическая модель зависимости изменяемости механических характеристик плотности ρ(x) и вязкости μ(x) от напряженности физического поля
. Предложена физико-математическая модель зависимости изменяемости механических характеристик плотности ρ(x) и вязкости μ(x) от напряженности физического поля 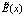 в низкоразмерной системе в виде [1, 2]:
в низкоразмерной системе в виде [1, 2]:
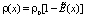 ,
, 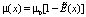 (1)
(1)
где 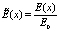 ,
, 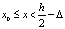 ,
, 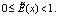
Учитывая вышеизложенные квантово-механические эффекты создана теория гидродинамики идеальной и вязкой жидкости в низкоразмерных системах 10–9 м ≤ h ≤10–4 м.
О качественном и количественном влиянии напряженности физического поля возникающего на границе «твердое тело-жидкость» в задачах гидромеханики в низкоразмерных системах
Рассмотрим низкоразмерную трубку радиусом R0 заполняемую жидкостью объемом V0. Определим высоту на которую поднимется жидкость в трубке, а также, как изменится характеристика массы жидкости за счет образования пустого пространства между твердым телом и жидкостью и влияния изменяемости плотности жидкости.
За счет влияния пристеночного физического поля радиус жидкости Rж, величина пустого пространства между стенкой и жидкостью Δ, а также, изменяемость плотности жидкости будут равны [1-4]:
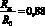 ,
, 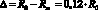 ,
,
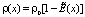 (2)
(2)
При этих условиях нами установлены следующие новые механические эффекты:
– за счет образования только пустого пространства высота подъема жидкости в трубке будет 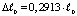 , а соответствующая ей выдавленная масса –
, а соответствующая ей выдавленная масса – 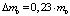 ,
,
– высота подъема жидкости в трубке, возникающая только за счет изменения плотности жидкости высота подъема жидкости в трубке будет 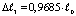 , а соответствующая ей выдавленная масса жидкости будет равна –
, а соответствующая ей выдавленная масса жидкости будет равна – 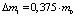 .
.
Таким образом, за счет суммарного влияния квантово-механических эффектов подъем жидкости по длине низкоразмерной трубки будет 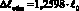 , а соответствующая ей выдавленная масса будет равна
, а соответствующая ей выдавленная масса будет равна 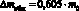 .
.
Определяющие уравнения гидродинамики вязкой жидкости с учетом квантово-механических эффектов в низкоразмерных системах
Учитывая квантово-механические эффекты, имеющие место между твердой стенкой и жидкостью и их проникающую способность вглубь жидкости, предложены следующие обобщенные уравнения Навье-Стокса движения вязкой жидкости в низкоразмерных системах [1-2]:
– уравнения движения сжимаемой вязкой жидкости в декартовых координатах:
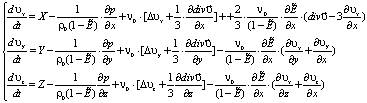 (3)
(3)
– уравнение неразрывности вида:
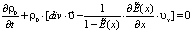 , для
, для 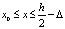 ,
, 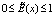 (4)
(4)
Здесь при x = x0, 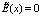 ; при
; при 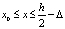 ,
, 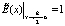 ;
; 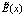 – экспериментально заданная линейная функция;
– экспериментально заданная линейная функция; 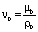 – коэффициент кинематической вязкости жидкости.
– коэффициент кинематической вязкости жидкости.
Движение несжимаемой вязкой жидкости между двумя параллельными пластинами в низкоразмерных системах
Граничная задача ламинарного течения несжимаемой вязкой жидкости между двумя неподвижными параллельными плоскими стенками, находящимися на расстоянии h друг от друга (10–9 м ≤ h ≤10–4 м) будет в видe [2]:
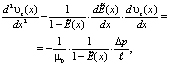
для 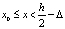 (5)
(5)
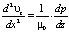 , для
, для 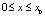 (6)
(6)
Граничные условия:
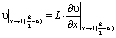 ,
,
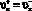 при
при 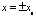 (7)
(7)
В этом случае распределение скорости движения вязкой жидкости в щели шириной h между двумя плоскими пластинами толщиной h будет в виде:
– в тонком слое (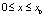 ) в виде:
) в виде:
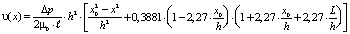 (8)
(8)
– в тонком слое (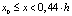 ) в виде:
) в виде:
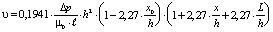 , (
, (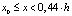 ). (9)
). (9)
Выводы
Отсюда видно, что течение вязкой жидкости в щели представляет собою течение стратифицированной жидкости. Установлен, также, характер распределения скорости по высоте в виде:
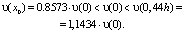 (10)
(10)
Во-вторых, установлено, что кванто-механические эффекты в низкоразмерной щели увеличивают среднюю скорость движения жидкости в два раза по сравнению с классическим его значением, т.е. 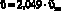 .
.

