Исследование и расчет динамических сил в переходных режимах работы конвейера основан на анализе волновых процессов, возникающих в ленте, представленной как упруго-вязкое тело, распространения в ней продольной волны упругих деформаций со скоростью, сопоставимой со скоростью звука.
Основой для проведения исследований динамических процессов является разработка математических моделей конвейера и его грузонесущей ленты, в наибольшей степени обеспечивающих ее адекватность физическим процессам, происходящим в период пуска и торможения, а также необходимую точность расчета и приемлемую их трудоемкость. При разработке таких моделей акцент делается на математическое представление конвейерной ленты как важнейшего элемента конвейера, обеспечивающего его надежность и технико-экономические показатели эксплуатации. Наиболее сложно динамические процессы при пуске и торможении протекают у протяженных ленточных конвейеров, к которым относятся и многоприводные, получающие все большее распространение на угольных шахтах.
Наиболее распространенной конструктивной схемой шахтных многоприводных конвейеров является схема, предусматривающая совместную работу головного барабанного привода с ленточными промежуточными.
При неравномерной или прерывистой загрузке участков грузонесущей ленты, ведомых промежуточными приводами, ее динамическое нагружение носит, как правило, кратковременный характер и опасности не представляет. В наибольшей степени динамическое нагружение приводных и грузонесущей лент конвейера проявляется при его пуске с незагруженной грузонесущей лентой и ее последовательной загрузкой. Для тяговых лент промежуточных приводов оно ничем не отличается от динамического нагружения лент коротких конвейеров, снижение которого достигается известными способами: использованием пусковых гидромуфт для асинхронных короткозамкнутых приводных электродвигателей или смягчением естественной характеристики двигателей с фазовым ротором.
Для грузонесущей ленты процесс пуска и ее динамическое нагружение происходят значительно сложнее. При пуске конвейера без груза основная нагрузка ложится на его головной барабанный привод, так как тяговые способности промежуточных приводов, при отсутствии на них груза, будут небольшими и достаточными лишь для преодоления их внутренних сопротивлений. По мере поступления груза на ленту, возрастают поочередно тяговые способности промежуточных приводов. При этом нагрузка на головной привод ступенчато снижется при резком изменении нагружения грузонесущей ленты. Это может вызвать возникновение в ленте опасных продольных колебаний, существенно увеличивающих в ней динамические усилия. Анализ и расчет динамических усилий в приводах и грузонесущей ленте многоприводного конвейера при неустановившихся режимах его работы могут быть осуществлены с использованием таких математических моделей, в которых математическое представление ленты отражает ее реологические свойства.
Представление конвейерной ленты как упруго-вязко-пластического тела [1, 4] позволяет при динамических нагрузках, воспринимаемых лентой, описывать происходящие в ней процессы с использованием одной из реологических моделей, представленных на рис. 1.
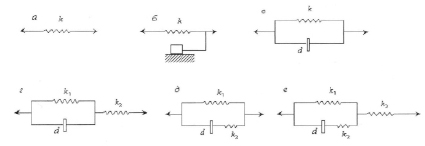
Рис. 1. Реологические модели, применяемые для описания механических свойств ленты при динамических нагрузках: а – упругая; б – упругая с трением Кулона; в – двухпарметровая Келвина; г – трепараметровая стандартная; д – трехпараметровая, состоящая из параллельно связанных моделей Максвелла и упругой модели; е – четырехпараметровая с упругим элементом, характеризующим мгновенную упругость
Для исследования и моделирования переходных процессов для ленты конвейеров может быть использована либо упругая модель (рис. 1, а), либо одна из вязко-упругих моделей: двухпараметровая модель Келвина (рис. 1, в); трехпараметровая стандартная (рис. 1, г), многопараметровая (рис. 1, д и е).
Реальные характеристики ленты лучше всего отражают многопараметровые модели. Однако, для практических целей наиболее часто используется модель Келвина и стандартная трехпараметровая модель. Ни одна их этих моделей не отражает полностью свойства ленты. Поэтому выбор той или иной модели диктуется поставленной при моделировании задачей и требуемой точностью результатов расчета.
Двухпараметровая модель Келвина состоит из параллельно соединенных элементов: упругого с постоянной k и гасителя колебаний с постоянной гашения d. Модель Келвина описывается уравнением
К = Е(ε + τк
), (1)
Трехпараметровая модель представляет собой соединение модели Гука и модели Келвина и состоит из двух упругих элементов и гасителя колебаний. Характеристика этой модели описывается уравнением [3]
К + τε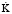
= Е∞(ε + τк
) (2)
В этих уравнениях:
К – напряжение;
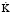– производная от напряжения;
τк – время запаздывания упругих деформаций при К = const, определенное опытным путем;
τε – время релаксации при ε = const, определенное опытным путем;
ε – относительное удлинение ленты;
– производная относительного удлинения ленты;
Е∞ – модуль упругой релаксации ленты.
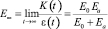, (3)
где K(t) – напряжение в рассматриваемый момент времени t;
ε(t) – относительное удлинение в момент времени t.
Еа и Е0 – модули упругости элементов с постоянными К1 и К2 соответственно.
Соотношение между этими модулями выражается уравнением
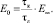(4)
Модель Келвина не описывает явление релаксации, что очевидно при подстановке в уравнение (1) 
= 0. Трехпараметровая стандартная модель описывает как явление растяжения, так и релаксации. Поэтому трехпараметровая модель имеет предпочтение перед моделью Келвина для моделирования переходных процессов многоприводного конвейера, характеризующихся волновыми процессами, происходящими в ленте, так как среда, описываемая моделью Келвина, является неволновой.
В математических моделях, описывающих ленточные конвейеры, лента может быть представлена как упруго-вязкий непрерывный стержень, на который действуют силы вдоль его главной оси. В этом случае движение ленты может быть описано двумя дифференциальными уравнениями в частных производных, одно из которых представляет условие равновесия сил, действующих на элементарный участок ленты, а другое – зависимость между напряжением в ленте и ее упругой линейной деформацией.
Условие равновесия сил выражается уравнением [2]:
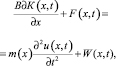(5)
где В – ширина ленты, м;
К (x, t) – напряжение в ленте, Н/м;
F (x, t) – сила, передаваемая от исполнительного органа привода на ленту, Н;
W (x, t) – сопротивление движению ленты и роликов, Н;
m(x) – линейная масса ленты, груза и вращающихся частей роликов для рассматриваемого участка ленты, кг/м;
x – составляющая продольной оси ленты, м;
t – временная составляющая, с;
u(x, t) – элементарное перемещение сечения ленты вдоль оси, Н.
Представляя ленту как линейно-упругое тело, зависимость между напряжением и линейной деформацией (растяжением) ленты можно записать уравнением
К = Eε, (6)
причем модуль упругости Е, как и напряжение К представлены отношением к линейной ширине ленты и выражены в Н/м.
Поскольку удлинение рассматриваемого элемента представляет собой элементарное перемещение сечения ленты, то второе уравнение имеет вид:
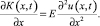(7)
Если не учитывать сопротивление движению W (x, t), то движение отрезка ленты, не контактирующего с исполнительными органами приводов, описывается известным волновым уравнением [2]:
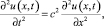(8)
где с представляет собой скорость распространения волны упругих деформаций.
Эта модель может быть использована для расчета скорости распространения волны напряжений на ведомых участках грузонесущей ленты и для выбора параметров ее натяжного устройства.
Для исследования прочностных свойств конвейерной ленты может быть использована стандартная трехпараметровая линейная модель.
После замещения в характеризующем ее уравнении (2) деформаций растяжения на перемещение сечений ленты, выраженных уравнениями (7) и (8), оно примет вид
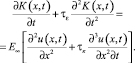(9)
Перемещение сечения ленты в этом случае можно представить как сложное движение, состоящее из движения ленты, рассматриваемой как жесткое тело, и упругих перемещений его сечений.
Перемещение сечения ленты в зависимости от x выражается суммой
U (x, t) = u (x, t) + ∫υ(x, t)dt. (10)
Тогда с использованием уравнений (5) и (10) получим выражение
m(x)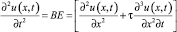
= = F(x, t) – W(x, t) – m(x)
, (11)
где υ представляет собой скорость перемещения ленты, представляемой как жесткое тело. Уравнение (11) может быть использовано для расчета скорости распространения волны напряжений в ленте. Условия равновесия в моделях, представляющих ленту в виде непрерывной системы, записываются в виде дифференциальных уравнений с частными производными. Их аналитическое решение приводит к необходимости введения допущений и упрощений, таких как: введение постоянного сопротивления движению ленты, постоянного усилия на исполнительном органе привода и ряда других, что приводит к получению сложных зависимостей. Это ограничивает применение указанных моделей для анализа приводных систем и натяжных устройств протяженных ленточных конвейеров, к которым относятся и многоприводные. Более простые решения и зависимости можно получить при использовании для динамических расчетов конвейеров дискретных моделей (рис. 2), которые дают приближенное представление конвейерной ленты как непрерывной системы. В этом случае лента делится на конечное число n отрезков с сосредоточенной массой, что приводит к дискретизации пространственной переменной трехпараметровой модели. Система уравнений с частными производными заменяется системой уравнений с простыми производными, в которых присутствует только функция времени. Точность решения будет зависеть от принимаемого количества отрезков. Ленту, как непрерывную систему, можно представить в виде граничного случая, когда количество отрезков стремится к бесконечности. Однако от количества отрезков зависит количество уравнений, а следовательно, время и стоимость расчетов. Компромиссный подход к этому при практических расчетах, использование для них РСЭВМ позволяет решить эту проблему.
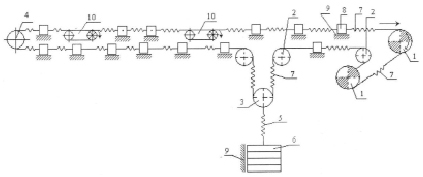
Рис. 2. Дискретная модель многоприводного конвейера: 1 – приводные барабаны головного привода; 2 – отклоняющийся барабан; 3 – натяжной барабан; 4 – концевой барабан; 5 – представление механизма натяжения в виде упругого (пружинного элемента); 6 – груз; 7 – упруго-вязкий элемент; 8 – сосредоточенная масса отрезка ленты; 9 – сопротивление движению в виде трения кулона; 10 – промежуточный привод
Рис. 3. Способы дискретного моделирования волновой системы непрерывного стержня: а – непрерывный стержень; б – модель Rayleigba; в – модель Лагранжа; г – несимметричная модель
Основные способы дискретного моделирования волновой (колебательной) системы конвейерной ленты как непрерывного стержня представлены на рис. 3.
Ошибка в определении частоты свободных колебаний для первых двух моделей обратно пропорциональна m2, для односторонней (рис. 3, г) модели пропорциональна п, принимая, что п – количество отрезков. Две первые модели, таким образом, являются более точными, а третья модель проще в описании, что делает ее предпочтительной в данном конкретном случае.
Уравнение равновесия (5) сил, действующих на отрезок ленты при этой модели, имеет вид
В[К(i + 1) – К (i)] + F1 = 
m(i) + W(t), (12)
где i – номер рассматриваемого отрезка.
Для стандартной трехпараметровой модели уравнение (9) в этом случае принимает вид
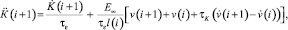(13)
где l(i) – длина отрезка ленты, м.
Сопротивление движению при дискретной модели может быть представлено в виде трения Кулона, возникающего от действия каждой из сосредоточенных масс грузонесущей ленты. Это дает возможность достаточно просто учитывать изменение сопротивления на участках, ведомых головным и промежуточным приводами. Вращающиеся массы приводных барабанов головного и промежуточных приводов, а также тяговые ленты промежуточных приводов представляются в модели как концентрированные массы, включенные между отрезками ленты.
Рассмотренная комплексная модель многоприводного конвейера может быть рекомендована для исследования переходных процессов в многоприводных конвейерах с использованием для этой цели РСЭВМ.