Нелинейная нагрузка является источником высших гармоник (ВГ) в СЭС при условии синусоидальности напряжения источника питания. ВГ приводят к различным негативным последствиям для элементов СЭС: чрезмерный нагрев проводов воздушных линий электропередачи (ЛЭП), ускоренное старение внутренней изоляции электрических машин и кабельных ЛЭП (включая чрезмерный нагрев и выход из строя нулевых жил кабелей на класс напряжения менее 1 кВ). Они способны вызвать значительную токовую перегрузку (перегрев) БСК, которая приведет к аварийным ситуациям (начиная с разрушения изоляции, вспучивания банок и заканчивая взрывом конденсаторной батареи). В стандартах ГОСТ IEC 60931-1-2013 и ГОСТ IEC 61921-2013 [1, 2] говорится, что конденсаторные батареи не допускается эксплуатировать при токовой перегрузке, превышающей номинальный ток установки в 1,3 раза. Рассмотрению этих и многих аспектов негативного влияния ВГ как на различные элементы, так и на всю СЭС целиком посвящено достаточно большое количество работ, например [3–5]. Учитывая эти аспекты, а также постоянный рост электроприёмников, имеющих нелинейную вольт-амперную характеристику, можно сказать, что актуальность проблемы влияния ВГ на СЭС не вызывает сомнений.
Согласно действующему в России стандарту на качество электроэнергии ГОСТ 32144-2013 [6] воздействие нелинейной нагрузки на СЭС характеризуется изменением величины и формы питающего напряжения (отклонением напряжения от идеальной синусоиды). Для их оценки используются следующие показатели качества электрической энергии:
– коэффициент n-й гармонической составляющей напряжения (определяется отдельно для каждой гармоники)
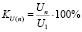 при n ≤ 40;
при n ≤ 40;
– общее содержание высших гармоник напряжения в СЭС
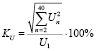 ,
,
где n – номер гармоники,
Un – действующее значение напряжения n-й гармоники,
U1 – действующее значение напряжения первой (основной) гармоники (при 50 Гц),
KU(n) – коэффициент n-й гармонической составляющей напряжения,
KU – суммарный коэффициент гармонических составляющих напряжения.
Теория и моделирование
Резонансные явления, так же как и ВГ, негативно сказываются на работе СЭС, так как они способны спровоцировать аварию, которая является следствием чрезмерного нагрева различных элементов сети (трансформаторов, ЛЭП, БСК) или вызвать пробой изоляции при возникновении коммутационных перенапряжений. Анализу резонансных режимов, возникающих на ВГ сети и определению частот, на которых возможен резонанс токов, посвящены работы [7–10].
Резонанс токов – это режим работы СЭС с параллельным соединением индуктивных и емкостных элементов. Цепи, в которых может возникнуть резонансный режим, называются резонансными контурами. Он характеризуется нулевым значением суммарной реактивной проводимости резонансного контура [11]. В качестве примера следует отметить, что резонанс токов способен возникнуть при подключении на одну секцию шин частотно-регулируемого электропривода (нагрузку, имеющую активно-индуктивный характер потребляемого тока) и БСК, имеющую емкостный характер тока.
Следует отметить, что резонансные условия практически не выполняются на основной частоте сети, однако на частотах, близких к частотам ВГ могут легко выполниться. Авторы работы [12] отмечают, что в большинстве случаев электротехнический персонал, обслуживающий сети не имеет четкого представления об условиях возникновения резонансов на ВГ при изменении конфигурации СЭС, поэтому при определенном сочетании включенных ячеек на подстанции возможен выход из строя силового электропривода по причине возникновения резонанса токов на частотах ВГ сети.
Рассмотрим СЭС (см. рис. 1). Схема замещения такой СЭС на основной частоте представлена на рис. 2, на ВГ – на рис. 3. В качестве нагрузки, являющейся источником ВГ в сети, рассмотрим частотно-регулируемый электропривод, который генерирует широкий спектр гармоник в СЭС. Также, к шинам 0,4 кВ подключена БСК, предназначенная для компенсации реактивной мощности и повышения коэффициента активной мощности нагрузки (cosφ) в сети.
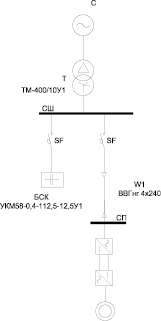
Рис. 1. Схема СЭС
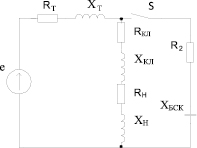
Рис. 2. Схема замещения СЭС на основной гармонике сети
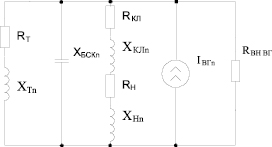
Рис. 3. Схема замещения резонансного контура СЭС (на ВГ)
Предлагаемый алгоритм. Численный эксперимент
Сопротивление трансформатора с ростом частоты увеличивается и в комплексном виде может быть представлено как
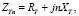
где RТ – активное сопротивление трансформатора,
XТ – индуктивное сопротивление трансформатора на основной частоте,
n – номер гармоники.
Аналогично можно записать и сопротивление кабельной линии в комплексном виде:

где RКЛ = r0L,
XКЛ = x0L,
r0, x0 – активное и индуктивное сопротивление кабельной ЛЭП на километр длины, Ом/км,
L – длина кабеля, км
Сопротивление БСК, наоборот, с ростом частоты уменьшается, т.е. имеет место следующее соотношение:
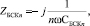
где CБСКn – емкость БСК на выбранной ступени,
ω = 2πf – циклическая частота,
f – частота питающей сети (50 Гц).
Емкость БСК (CБСКn) связана с величиной вырабатываемой реактивной мощности конденсаторной батареи (QБСК) следующим образом:
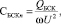
где U – напряжение сети.
По определению резонанса мы имеем равенство проводимостей параллельных ветвей сети, т.е. для нашего случая мы можем записать:
bL = bc.
Условия возникновения резонанса токов в рассматриваемой СЭС принимают следующий вид:

где LΣn – суммарная индуктивность СЭС на частоте n-й гармоники,
R1 – суммарное активное сопротивление кабельной линии и нагрузки,
R2 – активное сопротивление БСК.
Если в последнем выражении пренебречь активным сопротивлением конденсаторной батареи (R2), тогда условие резонанса примет следующий вид:
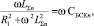
где ω – резонансная частота, рад.
Выразив из предыдущего выражения ω, получим формулу для определения резонансной частоты:
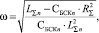
где RΣ – суммарное активное сопротивление СЭС.
Если пренебречь активным сопротивлением СЭС, тогда условие резонанса существенно упрощается и примет следующий вид:
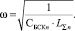
Мы получили резонансную частоту в радианах. Если мы хотим получить частоту в герцах, тогда можно воспользоваться следующей формулой:
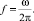
Рассмотрим на простом примере возможность возникновения резонанса. В СЭС, изображенной на рис. 1, может возникнуть резонанс токов, так как одновременно с решением проблемы компенсации реактивной мощности у нас образуется параллельный резонансный контур, в который входит нелинейная нагрузка с одной стороны, и БСК – с другой. В табл. 1 приведены параметры элементов СЭС необходимых для расчета всех возможных резонансных частот.
В рассматриваемой работе нелинейная нагрузка рассматривается как стационарно включенная, а изменение режима работы СЭС происходит посредством изменением степени компенсации реактивной мощности, а именно переключением ступеней БСК (рис. 4).
Кроме того, на этом же рисунке видно, что одновременно с увеличением степени компенсации уменьшается величина потребляемой реактивной мощности из системы. Рассмотрение именно такого режима работы необходимо для определения всех возможных резонансных частот для данной схемы.
Отметим основные допущения, которые были применены автором статьи при определении резонансных частот.
1. БСК была представлена емкостным сопротивлением (активное сопротивление не учитывалось ввиду его малости).
2. Частотно-регулируемый электропривод (частотный преобразователь) представлен источником тока с внутренним сопротивлением.
3. КЛЭП представлена в виде комплексного RL-сопротивления (без учета зарядной мощности).
Таблица 1
Паспортные данные трансформатора и кабельной линии
|
Трансформатор ТМ-400/10 У1 |
||||||||
|
Sном, кВА |
Рхх, кВт |
Ркз, кВт |
Uкз, % |
Iхх, % |
Rт, мОм |
Xт, мОм |
Uвн, кВ |
Uнн, кВ |
|
400 |
0,95 |
5,5 |
4,5 |
2,1 |
5,5 |
17,1 |
10,5 |
0,4 |
|
Кабельная линия ВВГнг 4х240 |
||||||||
|
r0, Ом/км |
х0, Ом/км |
Iдоп, А |
||||||
|
0,077 |
0,077 |
421 |
||||||
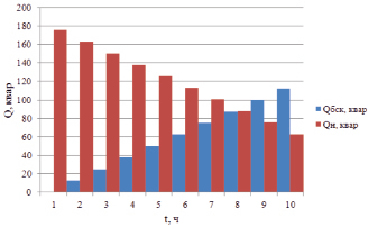
Рис. 4. График реактивной мощности нагрузки и ступеней БСК (за рабочую смену)
Таблица 2
Значения коэффициента активной мощности и резонансной частоты с учетом (f1рез) и без учета (f2рез) активной составляющей сопротивления элементов СЭС
|
QБСК, квар |
cos φ |
f1рез, Гц |
f2рез, Гц |
ε, % |
|
0 |
0,76 |
– |
– |
– |
|
12,5 |
0,783 |
1312,713 |
1312,818 |
0,008 |
|
25 |
0,807 |
928,15 |
928,299 |
0,016 |
|
37,5 |
0,83 |
757,767 |
757,949 |
0,024 |
|
50 |
0,853 |
656,19 |
656,401 |
0,032 |
|
62,5 |
0,876 |
586,866 |
587,101 |
0,04 |
|
75 |
0,898 |
535,688 |
535,946 |
0,048 |
|
87,5 |
0,919 |
495,908 |
496,187 |
0,056 |
|
100 |
0,939 |
463,84 |
464,137 |
0,064 |
|
112,5 |
0,956 |
437,277 |
437,593 |
0,072 |
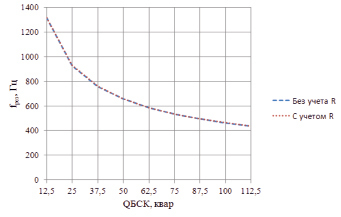
Рис. 5. График зависимости резонансной частоты от степени компенсации реактивной мощности
Предлагаемый алгоритм вычисляет: коэффициенты активной мощности нагрузки СЭС (как перед проведением компенсации реактивной мощности, так и после), коэффициенты загрузки питающего трансформатора (до и после компенсации), а также определяет резонансную частоту для каждого из режимов работы СЭС. Стоит отметить, что авторами производилось сравнение получившихся резонансных частот, определенных как с учетом активных составляющих сопротивления системы, так и без их учета, что нашло отражение в табл. 2.
Расчет показал, что погрешность определения частоты резонанса не превышает 0,1 %, если мы пренебрегаем активным сопротивлением резонансного контура. На рис. 5 приведены графики, наглядно показывающие нам, что погрешность определения резонансной частоты без учета активной составляющей сопротивления резонансного контура будет незначительной (оба графика совпадают). То есть при проведении практических расчетов мы вправе пренебречь активной составляющей сопротивления контура.
Выводы
На основании расчетов были определены все возможные частоты, на которых будет выполняться условие резонанса токов. Также, расчетным путем была определена погрешность определения резонансной частоты при пренебрежении активной составляющей проводимости контура, которая составила менее 0,1 %. Выявление резонансных частот необходимо для подбора и настройки фильтров, предназначенных для снижения уровня токов ВГ в сети (для фильтрации ВГ с частотами, близкими к резонансным). Кроме того, определение возможных частот резонанса необходимо для оценки целесообразности применения фильтров гармоник.

