Теория фракталов применяется при описании структуры неупорядоченных сред, например пористых сред, и описании протекающих в таких средах процессов. Движение примеси в потоке однородной жидкости описывается с использованием дифференциального уравнения дробного порядка [7]. Язык дробных производных применен при описании физических процессов стохастического переноса [9], при изучении деформационно-прочностных свойств полимерных материалов [1]. Диффузии дробного порядка посвящена работа [3]. Методам численного решения многомерного уравнения диффузии дробного порядка посвящены работы [5, 6, 10]. Задачи с сосредоточенной теплоёмкостью определённой величины на границе изучены в [8].
В данной работе рассматривается уравнение теплопроводности с переменными коэффициентами с дробной производной по времени с сосредоточенной теплоёмкостью определённой величины.
Постановка задачи. Устойчивость
В области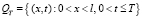 
будем рассматривать уравнение теплопроводности с дробной производной по времени с сосредоточенной теплоемкостью вида
,
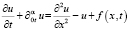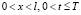, (1)
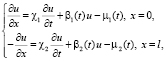(2)
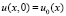, x ≥ 0, (3)
где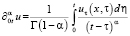 
– регуляризованная дробная производная порядка α, где 
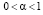. Коэффициенты удовлетворяют условиям: 
, 
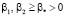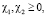
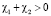. Устойчивость решения задачи (1)–(3) будем доказывать с помощью известного метода энергетических неравенств [8]. Для чего уравнение (1) умножаем на u(x, t) скалярно и получим тождество
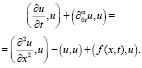(4)
В (4) скалярное произведение определено по формуле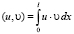 
и норма через него 
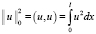. Первое и второе слагаемые в (4) нам дадут
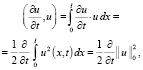
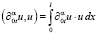. (5)
Для третьего слагаемого в (4) применяем интегрирование по частям:
.
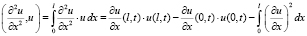Принимая во внимание граничные условия (2), из последнего можем записать:
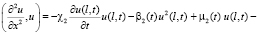
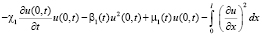. (6)
В (6) к слагаемым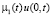 
, 
, 
, 
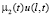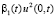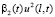применяется известное неравенство из [4, с. 172]. Первое и четвертое выражения в правой части (6) перепишем в виде
, 
.
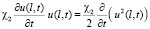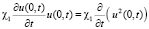Интеграл в правой части (6), четвёртый и пятый интегралы в тождестве (4) равны соответственно
, 
,
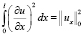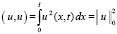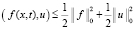. (7)
Поскольку интеграл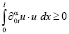 
, то, пренебрегая им в левой части (4) (неравенство только усилится), с учётом (5)–(7) получаем
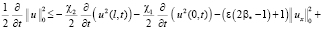
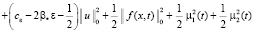. (8)
Полученное неравенство (8) теперь будем интегрировать по τ от 0 до t. С учетом начального значения (3) получаем для первого слагаемого:
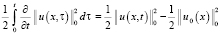. (9)
Для третьего и четвёртого выражений получим:
,
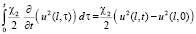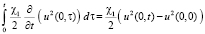. (10)
К выражениям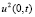 
, 
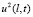также будем применять неравенство из [4, с. 172], а с учетом условия (3) запишем: 
, 
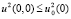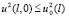. Для пятого, шестого и седьмого интегралов имеем
, 
, 
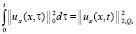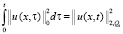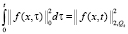. (11)
Учитывая (9)–(11) из (8) имеем
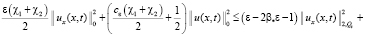
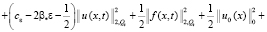
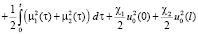. (12)
Сделаем обозначение в последнем неравенстве: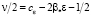 
и потребуем, чтобы выполнялось неравенство 
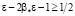. Также заметим, что 
, 
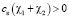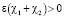ввиду условий 
, 
, 
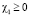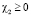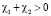. С учетом этого, сократив неравенство на 1/2, из (12) будем иметь
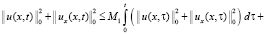
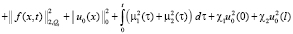. (13)
В (13) обозначим
.
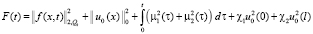Тогда из (13) можем записать
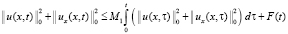. (14)
Введем в (14) обозначение: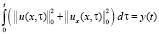 
, с учетом которого неравенство (14) перепишется в виде 
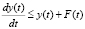. Далее, применяя лемму 1.1 для нестационарных задач ([4], стр.152), из последнего неравенства можем иметь неравенство: 
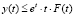. Теперь, учитывая последнее неравенство и введённые выше обозначения, записываем:
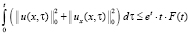. (15)
Учитывая (15), из неравенства (13) получаем неравенство:
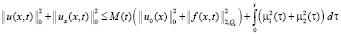, (16)
здесь M(t) – величина положительная, которая зависит от коэффициентов уравнения (1) и размеров области QT. Из полученной априорной оценки (16) можем сделать вывод, что решение задачи (1)–(3) устойчиво по начальному значению, граничным данным и правой части.
Разностная схема
Будем предполагать в дальнейшем, что решение задачи обладает требуемой по ходу изложения гладкостью. В замкнутой области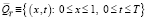 
строится сетка
,
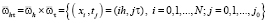где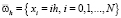 
, 
, 
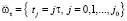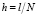– шаг сетки 
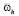по переменной x, N – число разбиений по x, 
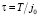– шаг сетки 
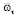по переменной t, j0 – число разбиений по t. Для уравнения (1) запишем разностное уравнение с параметром в виде
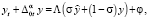(17)
где σ – параметр,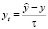 
, 
, 
, 
, 
, 
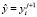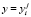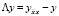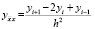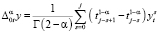– дискретный аналог дробной производной, 
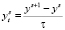. В классе достаточно гладких функций u(x, t) справедливо равенство: 
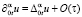(Шхануков М.Х. Доклады РАН. – 1996. – Т. 348. С. 746–748). Разностное уравнение (17) аппроксимирует уравнение (1) с точностью O(h2 + τ).
Аппроксимацию при x = 0 краевого условия (2)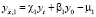 
, дающую точность O(h + τ), повышаем, следуя [8], до порядка O(h2 + τ). Получаем
,
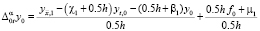где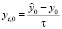 
, 
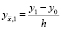. Аналогично, для (2) при x = l получаем
,
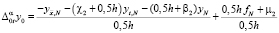где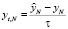 
, 
.
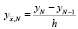Итак, разностный аналог задачи (1)–(3), дающий точность O(h2 + τ), запишется в виде
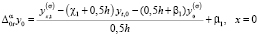, (18)
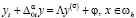, (19)
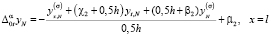, (20)
, 
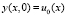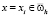, (21)
где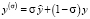 
, 
, 
, 
, 
.
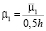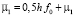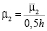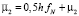Для достижения порядка аппроксимации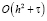 
при построении разностной схемы потребовалась достаточно высокая гладкость решения 
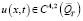, для чего необходимо 
.
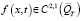Устойчивость разностной схемы
Для доказательства устойчивости построенной разностной схемы будем пользоваться принципом максимума. Для этого разностную схему (18)–(21) приведем к каноническому виду [8, с. 228]:
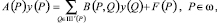(22)
где ω – сетка связная; Ш′(Р) – окрестность узла P, не содержащая сам узел P, F(P) – известная правая часть. Для коэффициентов (22) должны выполняться условия: A(P) > 0 для всех P∈ω; B(P, Q) > 0 для всех P, Q∈ω;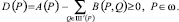 
Р∈ω. Рассмотрим случай σ = 1. Тогда (22) имеет вид: 
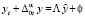. Расписав в индексной форме с учётом того, что 
, 
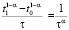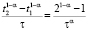, имеем
.
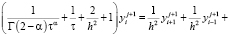
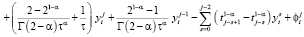Здесь коэффициенты:
,
, 
.
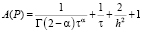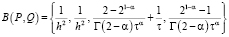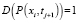Выполняются условия:
A(P) > 0, B(P, Q) > 0,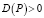 
. (23)
В точке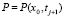 
для (23) будем иметь
.
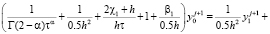
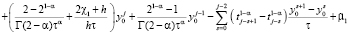Здесь коэффициенты равны
,
, 
.
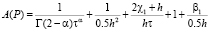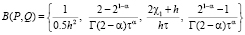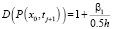С учетом неравенств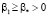 
, 
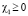имеем выполнение условий на коэффициенты:
A(P) > 0, B(P, Q) > 0,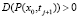 
. (24)
Аналогично, в точке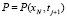 
для граничного условия (20) имеем
.
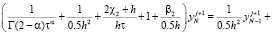
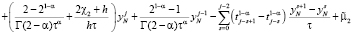Здесь коэффициенты имеют вид
,
, 
.
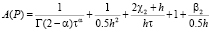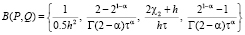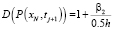С учетом условий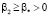 
, 
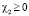имеем выполнение условий:
A(P) > 0, B(P, Q) > 0,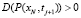 
. (25)
Из неравенств (23)–(25) на основании теоремы 3 [8, с. 228], для разностной задачи (18)–(21) следует справедливость оценки в норме пространства С: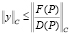 
, откуда следует устойчивость решения разностной схемы в равномерной метрике.