Получение расчетных формул
Расчет деформаций (εz и εθ) производился в цилиндрической системе координат (z, r, θ) и был основан на следующих предположениях: форма общих желчных протоков идеально цилиндрическая; стенка протоков представляет собой единое целое; материал стенки несжимаем [1]; отношение толщины стенки к радиусу протоков мало [10]; толщину стенки при 0 кПа можно измерить. Объём стенки V, таким образом, считался постоянной величиной, равной объёму V0 при давлении 0 кПа:
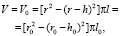(1)
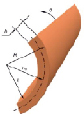
где r0, h0 и l0 – внешний радиус, толщина и длина сегмента протока, измеренные при давлении 0 кПа, r, h и l – внешний радиус, толщина и длина, измеренные при избыточном давлении (рис. 1, а).
В связи с тем, что стенка протоков считалась тонкой, радиальная компонента εr деформаций не рассматривалась. При определении продольных и кольцевых интрамуральных напряжений использовали канонические формулы Лапласа для упругой полой трубки [7]. Далее определяли эффективные упругие модул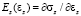и 
и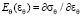 
.
Толщина стенки h при произвольном давлении вычислялась как
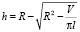, (2)
R и l – внешний радиус и длина соответственно при нагружении.
Величина измеренных и рассчитанных деформаций далее использовалась для вычисления кольцевых и продольных напряжений (рис. 1, б). В условиях равновесия связь напряжений и деформаций в кольцевом и продольном направлении определяли по формулам Лапласа. Согласно [9] кольцевое (оно же окружное) напряжение σθ, уравновешивающее избыточное внутреннее трансмуральное давление равно
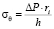, (3)
где ΔP – трансмуральное давление, а ri = R – h – внутренний радиус.
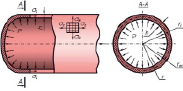
Избыточное давление рассчитывали по известному гидростатическому. Поскольку ось протока в ванне с физиологическим раствором проходила через основание колонны давления (рис. 1, в), то по закону Паскаля трансмуральное давление совпадало с гидростатическим, приложенным к сегменту:
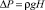, (4)
здесь ρ – плотность жидкости, g = 9,81 м•сек–2 – ускорение свободного падения, H – высота столба жидкости.
Продольное напряжение σz вычислялось как
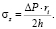(5)
Несмотря на то, что деформации были достаточно большие, для простоты они вычислялись как деформации Коши [2]. Величина деформации в кольцевом направлении определялась как
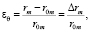(6)
где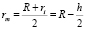 
– среднекольцевой радиус (внешний радиус за вычетом половины толщины протока) при различных приложенных напряжениях, l0m – среднекольцевой радиус при 0 кПа.
Относительная деформация в продольном направлении рассчитывалась как
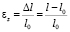, (7)
здесь l – длина сегмента протока, измеренная под давлением, l0 – соответствующая длина, измеренная при 0 кПа.
В результате использовались следующие формулы для расчёта кольцевых и продольных деформаций εθ, εl и напряжений σθ, σl:
, 
,
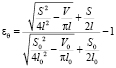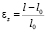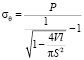и 
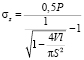. (8)
В итоге расчётная схема для определения внутренних напряжений и упругих дифференциальных модулей Ez и Eθ полых органов при механических испытаниях инфузионным методом имела вид (рис. 2).
Условные обозначения: V = V0 – объём стенки сегмента органа, измеренный между специальными метками; R – внешний радиус; l – длина; S – площадь; ri – внутренний радиус; rm – среднекольцевой радиус; h – толщина стенки; σz, εz – напряжение и относительная деформация в продольном направлении; σθ, εθ – напряжение и относительная деформация в кольцевом (окружном) направлении; ρ – плотность, H – высота столба жидкости; ΔP – избыточное давление.
а) б) в)
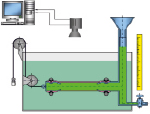
Рис. 1. Сегмент стенки протока (а). Схема возникновения напряженно-деформированного состояния (НДС) в стенке протока под действием внутрипротокового давления P (б). Экспериментальная установка для исследования упругих свойств желчных протоков в условиях, близких к физиологическим (в)
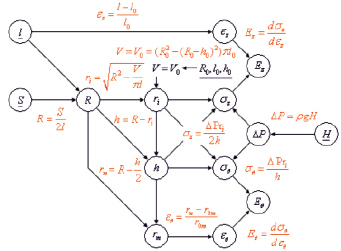
Рис. 2. Последовательность расчётов при вычислении деформаций, напряжений и упругих модулей общего желчного протока
Величины, определённые путём прямых измерений – подчёркнуты.
Подготовка образцов и механические испытания
Механические испытания были проведены инфузионным методом [4, 6]. Такой тип испытаний даёт больше достоверной информации, чем одноосное растяжение изотропных материалов [8], хотя последний более прост и доступен. Исследование желчных протоков при внутреннем давлении в условиях, близких к физиологическим, позволило получить более достоверную информацию об их деформационном поведении.
Измерения проводились в пластиковом контейнере в среде буферного раствора Кребса – Рингера с pH = 7, моделирующем физиологические жидкости организма при температуре 370 С. В этом же растворе образцы хранились до испытаний. Исследования выполнены на трупных органах. Взятие и подготовку органов проводили по стандартной методике. Резецированный участок холедоха отмывали струёй проточной воды и освобождали от слоя жировой клетчатки. Вырезка органов осуществлялась как можно ближе к моменту смерти. Для минимизации мышечных сокращений в 1 л раствора добавлялось 0,1 г Ca2+ связывающего агента EGTA. В качестве инфузионной системы использовались комплектующие от стандартного устройства для вливаний лекарственных растворов SFM Hospital Products GmbH. Проксимальный конец фрагмента протока соединялся с канюлей – полой трубкой системы. Нагнетание давления осуществлялось с помощью колонны гидростатического давления.
Другой конец, ближайший к сфинктеру Одди, как можно дистальнее перевязывался специальной легирующей нитью с покрытием, снижающим прорезывание тканей и прочно удерживающей узлы. Величина трансмурального давления определялась по высоте столба жидкости и изменялась ступенчато от 0 до 10 кПа (1 кПа = 10 см H2O) с шагом 1 кПа. Изображение протока под избыточным давлением записывалось на видеокамеру Nikon CoolPix 5600 и подавалось на персональный компьютер. Далее захваченное изображение преобразовывалось в оттенки серого и обрабатывалось графическими пакетами SigmaScan Pro 5.0 или ImageJ. Эти программы позволяют работать практически с любыми типами изображений, получаемых с внешних устройств. Кроме того, они имеют удобный интерфейс, созданный специально для учёных и специалистов, не являющихся экспертами в области обработки изображений, позволяют быстро получить необходимую информацию об изображении и сократить время проведения исследований. Замер относительных деформаций в продольном направлении производился при помощи калиброванной координатной сетки. Чтобы исключить краевые эффекты, длина и площадь сегмента протока при канюлировании измерялись между двумя специальными метками, нанесёнными на образец на определённом расстоянии от его концов. Для определения величины деформаций в кольцевом направлении внешний диаметр протоков вычислялся по измеренным длине и площади. Начальная толщина исследуемых препаратов определялась с помощью нескольких измерений микрометром, по которым вычислялось среднее значение. Перед основными испытаниями для стабилизации свойств изучаемого образца применяли предподготовку посредством многократного растяжения до деформации, составляющей 50 % от максимальной.
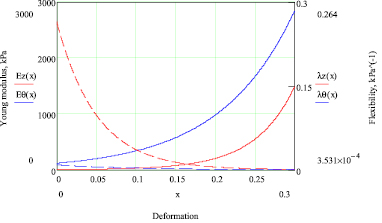
Рис. 3. Упругие дифференциальные модули Юнга E и коэффициенты податливости λ общего желчного протока в продольном (––) и кольцевом (––) направлениях в зависимости от величины относительной деформации
Обсуждение результатов измерений
В результате испытаний были получены зависимости напряжение – деформация и рассчитаны численные значения дифференциальных модулей упругости стенки протока в кольцевом и продольном направлении (рис. 3). Для всех органов, отобранных для исследований, кривые напряжение – деформация были идентичны. Кривые существенно нелинейны и сдвинуты относительно друг друга по оси деформаций. Это означает, что желчные протоки обладают анизотропными механическими свойствами, класс упругой симметрии – ортотропия, и легче растяжимы в продольном, чем в кольцевом направлении. Кривые напряжение – деформация взятых образцов стенки желчных протоков в обоих направлениях имеют характерный J – вид типичный для полых органов, например крупных артерий [3, 5], что косвенно свидетельствует о коллаген-эластиновой природе пассивных механических свойств стенки желчного протока. Численно диаграммы могут быть описаны экспоненциальной функцией σ = α(eβε – 1), а значения коэффициентов α и β – найдены с помощью функции нелинейной регрессии общего вида genfit, встроенной в среду MathCAD 13.0. Упругие модули были определены дифференцированием соответствующих регрессионных зависимостей. Данный способ аппроксимации оказался эффективен и показал высокую точность. В результате в продольном направлении установлено: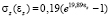 
кПа и 
кПа 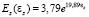(коэффициент достоверности регрессии 0,99), в кольцевом – 
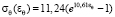кПа и 
КПа 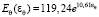(коэффициент достоверности регрессии 0,98) соответственно. Коэффициенты податливости определялись как 
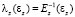и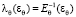 
(рис. 3). Упругие модули стенки общего желчного протока учитывались далее при компьютерном моделировании (численном анализе корреляции механического воздействия и билиарной боли).