Обычно для обработки цифровых сигналов применяют дискретное преобразование Фурье (ДПФ; английский термин – Discrete Fourier Transform, DFT) [1, с. 251]. Данный вид преобразования при анализе стационарных сигналов даёт достаточно точные результаты. Однако в анализе нестационарных сигналов он имеет существенный недостаток, связанный с тем, что дискретное преобразование Фурье неявно подразумевает периодическое продолжение исследуемого фрагмента сигнала. Это приводит к так называемому эффекту растекания спектра, вместо узкого пика получается сложный спектр, где могут содержаться все возможные частоты. Для уменьшения этого эффекта используют оконное преобразование Фурье, но и здесь возникает трудность с выбором ширины окна [1, с. 272].
В настоящее время в энергетике, и в том числе для расчета нестационарных режимов систем электроснабжения (СЭС), находит широкое применение математический аппарат вейвлет-преобразование (ВП), поскольку лишен ряда недостатков, присущих преобразованию Фурье [2–4]. Вейвлет-преобразование даёт возможность лучше рассмотреть элементы сигнала, присутствующие на коротком промежутке времени [5, с. 30].
Его суть заключается в скалярном перемножении исследуемой функции на анализирующую функцию [5, с. 55].
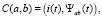 (1)
(1)
где i(t) – исследуемая функция,
Ψab(t) – анализирующая функция.
В качестве анализирующей функции выступает набор вейвлет-функций, получаемых из базисной посредством сжатия растяжения функции при помощи параметра а и сдвига по временной оси при помощи параметра b [5, c. 55].
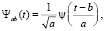 (2)
(2)
где 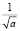 – обеспечивает независимость нормы функции от масштаба a,
– обеспечивает независимость нормы функции от масштаба a,
ψ(t) – функция материнского вейвлета.
Это выражение справедливо для непрерывного вейвлет-преобразования (НПВ). Оно позволяет получить трёхмерный спектр, где наглядно представлены частоты, присутствующие в сигнале, их время присутствия и масштаб (аналог амплитуде).
Данный вид ВП является избыточным и требует большого количества математических операций. Поэтому на практике чаще всего применяются дискретное вейвлет-преобразование (ДВП) и пакетное вейвлет-преобразование (ПВП). Они осуществляются разложением исходной, анализируемой функции на составляющие.
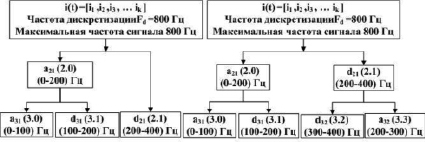
Главным принципом дискретного вейвлет-разложения является рекурсивное определение последующих элементов более глубокого уровня разложения. В этом случае исследуемый сигнал пропускается через низкочастотный (НЧ) и высокочастотный (ВЧ) вейвлет-фильтры, которым соответствуют масштабирующая функции ψ(t) и вейвлет-функция ψ(t). На выходе имеем две последовательности, первую аппроксимирующих и вторую детализирующих коэффициентов. Затем последовательность аппроксимирующих коэффициентов опять пропускается через высокочастотные и низкочастотные фильтры. На выходе получаем набор аппроксимирующих и детализирующих коэффициентов на следующем уровне разложения и т.д. Весь процесс разложения протекает по схемам, представленным на рис. 2 [6, c. 46–47]. Так же при выбранной частоте дискретизации каждый из этих наборов вейвлет-коэффициентов, на каждом уровне, будет отвечать за свой диапазон частот, как показано на рис. 2.
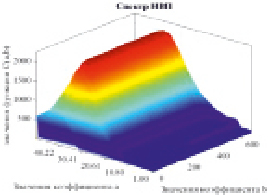
Рис. 1. Спектр непрерывного вейвлет-преобразования
а) б)
Рис. 2. Схема вейвлет-преобразования: а) для дискретного вейвлет-преобразования, б) для пакетного вейвлет-преобразования
При дискретном вейвлет-разложении сигнал тока может быть записан через вейвлет-коэффициенты.
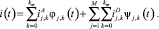 (3)
(3)
На основе равенства Парсеваля может быть вычислено действующее значение тока в заданном диапазоне частот.
В первый диапазон частот аппроксимирующего коэффициента 2 уровня разложения попадает основная частота 50 Гц. Отсюда действующее значение основной частоты можно вычислить как [7, с. 88]:
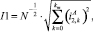 (4)
(4)
где N – количество отсчетов исследуемого дискретного сигнала.
Действующие значения токов высших 3 и 7 гармоник при дискретном вейвлет-преобразовании могут быть вычислены соответственно через детализирующие коэффициенты 2 уровня разложения и детализирующие коэффициенты 1 уровня разложения.
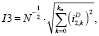 (5)
(5)
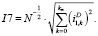 (6)
(6)
Из-за того, что высокочастотный и низкочастотный вейвлет-фильтры не являются идеальными, на границе двух частотных коридоров, одна частотная полоса немного наслаивается на другую. Это в свою очередь приводит к погрешности в расчетах [8]. Что приводит к необходимости выбирать тот или иной тип вейвлета в зависимости от поставленной задачи. В данной работе погрешности от выбора типа вейвлета рассматриваться не будут.
Так же при дискретном или пакетном вейвлет-преобразовании погрешность возникает из-за краевого эффекта, который появляется при недостаточной длине реализации сигнала. Для устранения этой погрешности существуют различные способы позволяющие увеличить длину реализации сигнала. В рамках данной статьи будут рассмотрены способы, встроенные в программный комплекс MATLAB [9]:
- sym или sumh – симметричное заполнение по граничным значениям (полуточечное);
- symw – симметричное заполнение по граничным значениям (полное);
- asym или asymh – асимметричное заполнение по граничным значениям;
- asymw – асимметричное заполнение по граничным значениям (полное);
- zpd – дополнение данных нулями;
- spd или sp1 – интерполяция первого порядка;
- sp0 – интерполяция нулевого порядка;
- per – периодизация.
Для того чтобы выяснить, какой из этих способов вносит меньшую погрешность в расчет, произведём расчет действующих значений тока разных частотных составляющих при разных типах увеличения длины реализации сигнала.
Для численного эксперимента зададим сигнал тока формулой
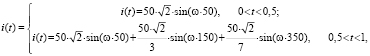 (7)
(7)
где 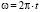 .
.
Данный сигнал тока содержит частоты 50, 150 и 350 Гц. Далее производим дискретное вейвлет-преобразование исследуемого сигнала, разложив его на частотные диапазоны, для анализа используем вейвлет Добеши 40 порядка (db40), как наиболее точный.
После чего вычисляем действующие значения токов каждой частотной компоненты, используя различные типы увеличения длины реализации сигнала. Расчет действующих значений производим по формуле (5, 6). И затем рассчитываем погрешность расчета.
Все полученные результаты сведены в таблицу.
Результаты численного эксперимента
|
Способ увеличения длины реализации сигнала |
Действующие значения токов, посчитанные аналитически |
Действующие значения токов, посчитанные через вейвлет-коэффициенты |
Погрешности расчетов действующих значений через вейвлет-коэффициенты |
||||||
|
I1, А |
I3, А |
I7, А |
IW1, А |
IW3, А |
IW7, А |
E1, % |
E3, % |
E7, % |
|
|
sym или sumh |
50 |
11,79 |
5,05 |
84,723 |
17,76 |
7,343 |
69,44 |
50,74 |
45,39 |
|
symw |
84,819 |
19,49 |
7,394 |
69,64 |
65,36 |
46,39 |
|||
|
asym или asymh |
84,499 |
18,57 |
7,784 |
68,99 |
57,58 |
54,11 |
|||
|
asymw |
141,43 |
17,39 |
7,251 |
182,8 |
47,59 |
43,56 |
|||
|
zpd |
50,005 |
11,59 |
5,448 |
0,0009 |
1,59 |
7,87 |
|||
|
spd или sp1 |
54,25 |
11,42 |
5,153 |
8,5 |
3,10 |
2,03 |
|||
|
sp0 |
54,910 |
11,46 |
5,203 |
9,82 |
2,70 |
3,01 |
|||
|
per |
50,019 |
11,66 |
5,136 |
0,039 |
1,07 |
1,68 |
|||
Выводы
По полученным результатам можно сделать вывод, что только способ увеличения длины реализации сигнала при помощи периодизации даёт возможность с достаточной точностью рассчитывать действующие значения токов различных гармонических составляющих, дополнение данных нулями тоже даёт неплохие результаты, но только при расчете действующих значений низких частот.

