Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Современные устройства функциональной электроники по своим энергическим характеристикам далеки от совершенства: удельные энергозатраты на один бит обрабатываемой информации на 7–9 порядков превышают теоретический предел. Поэтому не ослабевает интерес к идее создания электронных устройств с использованием молекулярных сред. Ввиду трудностей, связанных с использованием отдельных молекул в качестве элементов устройств (невозможности возбудить необходимый дискретный уровень энергии, дизактивацией состояний молекулы, малыми временами жизни возбуждений), одним из основных подходов явилось запараллеливание молекул в ансамбли (кристаллы, тонкие плёнки, композиты). Особый интерес представляют ультратонкие плёнки молекулярных кристаллов, содержащих сильно полярные группы и связи. Характерные особенности таких систем – это влияние на их параметры поверхности и границ раздела, а также значительный линейный и нелинейный отклики молекулярных характеристик на внешние воздействия. Для того чтобы управлять микропараметрами анизотропной среды с помощью макрополя, необходимо уметь находить динамические и электрические характеристики: частоты и формы колебаний молекул, их поляризуемости, действующее на молекулу внутреннее поле, линейную и нелинейную восприимчивость.

Целью настоящей работы являлось установление взаимосвязи между микро- и макропараметрами, а также определение этих параметров для ультратонких молекулярных плёнок нелинейных кристаллов.

В качестве объектов исследования были выбраны молекулярные кристаллы и кристаллические плёнки метанитрозамещённых бензола, которые имеют полярные направления, и им присущи свойства, описываемые тензорами третьего ранга (например, генерация второй оптической гармоники, пьезоэлектричество). Эти обьекты отличаются гигантскими нелинейными восприимчивостями в оптическом диапазоне, что определяет их применение в устройствах записи и отображения информации, модуляторах, дефлекторах, преобразователях излучения и т.д.

Эффективными методами изучения динамических и электрооптических характеристик молекулярных кристаллов и сверхтонких кристаллических плёнок являются методы комбинационного рассеяния света (КРС), генерации второй оптической гармоники (ГВГ), рефрактометрии и рефлексометрии; молекулярной динамики, математического моделирования. Рассмотрим, каким образом они использовались для исследования физических свойств объектов.

Для извлечения полной и достоверной информации из оптических спектров необходимо решить динамическую задачу, т.е. найти все собственные частоты и собственные векторы колебаний системы. Однако особый интерес представляют колебательные моды при нулевом волновом векторе (фундаментальные колебания), так как они могут сравниваться с экспериментальным спектром КРС или инфракрасного поглощения света. Энергия решётки и спектр малых частот рассчитывались в приближении атом-атомных потенциалов, а поскольку молекулы метанитробензолов имеют значительные мультикольные молекулы, то учитывались и электростатические взаимодействия [1].

Динамика сверхтонких слоёв вычислялась в модели пластины [2].

Связь между макро- и микропараметрами среды осуществляется посредством учёта внутреннего (или локального) поля 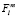, действующего на m-молекулу:

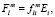(1)

где Ei – i-я компонента макроскопического электрического поля, f(m) – тензор коэффициентов локального поля, который в самом общем виде может быть представлен схематически как

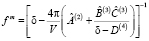, (2)

где δ – символ Кронекера, V – объём элементарной ячейки;

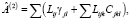(3)

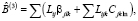
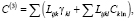
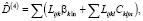
γjl, Cjkl – дипольная и квадрупольная поляризуемости m-ой молекулы,

βjlk и Cijln – её дипольная и квадрупольная гиперполяризуемости; Lij, Lijk, Lijkl – диполь-дипольная, диполь-квадрупольная и квадруполь-квадрупольная решёточные суммы (анизотропный структурный фактор Лоренца).

Включая в рассмотрение частоту возбуждающего излучения ω и ограничиваясь дипольным приближением, получим из (2) [1]:

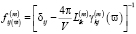. (4)

Тензор f и определяет связь между микро и макропараметрами среды. Так, макроскопическая линейная диэлектрическая восприимчивость молекулярного кристалла или кристаллической плёнки равна

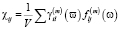. (5)

Величины χ в (5) определяют всю линейную кристаллооптику: абсолютную интенсивность линий комбинационного рассеяния и инфракрасного поглощения, процессы отражения и преломления света. Ещё в большей степени от f зависит нелинейная восприимчивость кристаллов и плёнок, которая характеризует нелинейные процессы, в частности генерацию второй оптической гармоники. Она определяется через нелинейную гинерполяризуемость молекулы 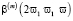– (2ϖ – частота выходящего из образца света) и уже три тензора локального поля [1]:

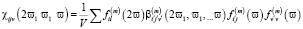. (6)

Рассмотрим результаты исследования динамических и оптических параметров молекулярных плёнок кристаллов м-нитрозамещённых бензола. Эти кристаллы принадлежат пространственной группе Pna21 и имеют 4 молекулы в элементарной ячейке, поэтому внешние решеточные колебания объёмных образцов при нулевом волновом векторе разделяются по типам симметрии следующим образом:

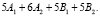
Все они активны в спектрах КРС и измерены ранее [1, 3, 4] с помощью поляризационной техники. Для вычисления спектра частот решеточных колебаний использовались атом-атомные потенциалы, подобранные ранее из сравнения экспериментальных и рассчитанных данных при исследовании не только объёмных кристаллов, но и молекулярных плёнок бензола и адсорбированных слоёв этана на графите [5]. Поскольку исследуемые в работе объекты имеют сильную анизотропию и значительные мультипольные моменты, был разными способами исследован вклад от мультипольных взаимодействий. Например, для кристалла м-нитробромбензола известно распределение зарядов [6], поэтому возможен как прямой расчёт кулоновского взаимодействия между атомами, так и определение мультипольных моментов молекулы с последующим нахождением членов мультипольного разложения энергии решётки. И прямой расчёт с радиусом суммирования 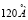, и расчёт на основе мультипольного разложения при суммировании по атомным подрешёткам – дают одинаковое значение электростатической энергии м-бромнитробензола, равное – 4 ккал/моль (это 18 % от суммарного рассчитанного значения энергии решётки – 23,4 ккал/моль (эксперимент даёт – 23,7 ккал/моль).

При расчёте динамики плёнки в модели пластины выбор её минимальной толщины определялся радиусом сходимости действующих сил и необходимостью иметь в её центральной области молекулу с таким же окружением, как и в объёмной структуре. Равновесное положение молекул м-нитробензолов на поверхности незначительно отличалось от их положений в центре ячейки, а энергия связи составляла 70 % от объёмной. Анализ результатов расчёта фононного спектра проводился путём рассмотрения собственных векторов полной динамической матрицы при переходе от объёмных молекул к поверхностным (по слоям). В табл. 1 приведены частоты решеточных колебаний метахлорнитробензола, измеренные методом КРС и рассчитанные для объёмных кристаллов и поверхностных слоёв.

Из таблицы видно, что значения квадратичных нелинейных восприимчивостей м-нитрозамещённых бензола, рассчитанные на основе найденных молекулярных нелинейных поляризуемостей и тензоров локального поля, хорошо согласуются с экспериментальными.

Линейная зависимость диэлектрической восприимчивости (5) от тензора локального поля, достаточная простота измерения коэффициентов рефракции прозрачных кристаллов позволяет использовать для проверки корректности расчёта локального поля данные по показателям преломления вещества n(ϖ). Для этого достаточно рассчитать диэлектрическую проницаемость ε(ϖ) по частоте ϖ видимого света по известной формуле

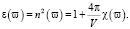
Для сверхтонкой пластины вычисляются тензоры эффективной поляризуемости для молекул на поверхности и вблизи неё, а также компоненты тензора L структурного фактора, входящие в формулы (4), для плоских молекулярных решёток по ранее разработанной методике.

Для экспериментального определения показателей преломления поверхностного слоя использовался разработанный ранее [27] лазерный поляризационный рефлектометр, предназначенный для измерения параметров шероховатостей сверхгладких диэлектрических пластин с помощью регистрации индикатрис рассеянного поверхностью света. В табл. 3 представлены коэффициенты тензора локального поля f и показатели преломления м-нитрозамещённых бензола в объёме (v) и на поверхности (s) (в системе осей индексов рефракции).

Как видно из табл. 3, показатели преломления в приповерхностном слое уменьшились по сравнению с объёмными, найденными для той же частоты падающего света, что, несомненно, связано с релаксацией и реконструкцией поверхности вследствие изменения структуры и внутреннего поля, а также обработки образца.

Таким образом, в работе исследованы фононные спектры и электрооптические параметры объёмных нелинейных кристаллов и тонких молекулярных плёнок. Удовлетворительное согласие между рассчитанными и экспериментальными данными позволяет надеяться на использование данного метода для поиска исследования других сложных систем с необычными характеристиками. Разработанная модель локального поля позволила установить связь между макро- и микроскопическими параметрами кристаллов и сверхтонких плёнок и подбирать эти параметры, не проводя громоздких экспериментов.