Накопленный к настоящему времени экспериментальный материал по изучению ранней стадии перехода от ламинарного к турбулентному режимам обтекания стимулирует создание новых и применение уже имеющихся методов математического моделирования этого важного этапа потери устойчивости сверхзвукового потока. В последние годы проводится углубленное изучение ряда методов эволюции возмущений в сверхзвуковых пограничных слоях сжимаемого газа. Эти работы можно разделить на две группы. В первой группе развиваются методы прямого численного моделирования систем уравнений в частных производных. Во второй расчеты проводятся в рамках традиционного метода возмущений, сводящегося к решению систем обыкновенных дифференциальных уравнений для средних характеристик и малых возмущений. Далее применяются положения слабонелинейной теории устойчивости, и исследования проходят на основе модельного подхода изучения взаимодействия в трехволновых системах (триплетах). Физическое обоснование такого моделирования заключается в изучении эволюции одной волны в силовом поле двух других волн, проходящее в условиях синхронизации их фаз.
Амплитудные уравнения для таких трехволновых систем получены при использовании стандартной процедуры осреднения и условия разрешимости [1].
Связь теории и эксперимента проходила в тесном сотрудничестве расчетной группы с исследовательским коллективом экспериментаторов, работающих на сверхзвуковой малотурбулентной аэродинамической трубе Т-325 ИТПМ им. С.А. Христиановича СО РАН, где уже длительное время изучают состав и продольную динамику как вводимых искусственно (контролируемых), так и естественных возмущений [2].
К настоящему времени первый раздел достаточно изучен – при невысоком начальном уровне возмущений реализуется субгармоническая неустойчивость, закономерности которой качественно и количественно описываются нелинейной моделью взаимодействия в резонансных триадах [1]. В отличие от первого, раздел изучения динамики естественных возмущений значительно менее популярен и соответственно – исследован.
В настоящее время четко установлено, что динамика развития естественных возмущений отличается от динамики развития контролируемых. Для них фиксируется широкий спектр частот при полном отсутствии данных об азимутальном составе компонент спектра, а перераспределение энергии осуществляется не только в субгармоническую область, но и в область высоких частот (обертонов). В этих условиях наряду с рассмотрением синхронизованных частотных триплетов возникает необходимость удовлетворить условиям фазового синхронизма и по азимутальным волновым числам.
Работа проведена в два этапа. Предварительно была подробно изучена принципиальная возможность моделирования взаимодействия в триплетах естественных возмущений произвольного азимутального состава. На втором этапе последовательно изучены взаимодействия в так называемых групповых триплетах, составленных из нескольких простых. В окончательном варианте, который представлен в данной работе, задействовано 12 синхронизированных частот, общее число простых триплетов, входящих в групповой, равнялось 36. Моделировались два набора синхронизованных азимутальных чисел, в которых основными несущими компонентами являются трехмерные волны, имеющие максимальные инкременты внутри нейтральной кривой при начальных числах Рейнольдса Re = 300 и 600.
Параметры [2] являлись отправными при расчетах – рассмотрен пограничный слой на непроницаемой теплоизолированной пластине под нулевым углом атаки при числе Маха М = 2, γ = 1,4, температуре торможения 310 К, числе Прандтля s = 0,72 и единичном числе Рейнольдса Re1 = 12,5×106 m-1. Интервал продольных чисел Рейнольдса соответствовал экспериментальному, введено расчетное число Рейнольдса 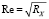 .
.
Основные соотношения и методы решения
Основные положения нелинейной модели взаимодействия возмущений в трехволновых резонансных системах в пограничных слоях сжимаемого газа подробно изложены в [1]. Необходимо перечислить основные положения используемого метода возмущений. Рассматривается возмущенное поле скоростей 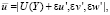 плотности
плотности 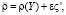 давления
давления 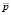 =
= 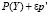 и температуры
и температуры 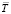 сжимаемого газа,
сжимаемого газа, 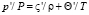 в безразмерных координатах (X, Y, Z) = (x, y, z)/δ (δ =
в безразмерных координатах (X, Y, Z) = (x, y, z)/δ (δ = 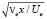 – характерный линейный масштаб). Здесь ε – масштаб пульсационного поля (ε << 1); e – индекс параметров на внешней границе; величины со штрихами и без штрихов – пульсационные и средние величины). Решение строится с помощью двухмасштабного разложения продольной координаты, вводятся «быстрый» и «медленный» масштабы (X и ξ = εX), характеризующие разницу скоростей изменения фазы и амплитуды возмущений.
– характерный линейный масштаб). Здесь ε – масштаб пульсационного поля (ε << 1); e – индекс параметров на внешней границе; величины со штрихами и без штрихов – пульсационные и средние величины). Решение строится с помощью двухмасштабного разложения продольной координаты, вводятся «быстрый» и «медленный» масштабы (X и ξ = εX), характеризующие разницу скоростей изменения фазы и амплитуды возмущений.
Решения для волн записываются в виде суперпозиции линейных компонент и составляющих более высокого порядка
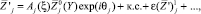 j = 1, 2, 3,
j = 1, 2, 3,
где 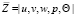 , A – медленно меняющаяся амплитуда; к.с. – комплексно-сопряженные величины;
, A – медленно меняющаяся амплитуда; к.с. – комплексно-сопряженные величины; 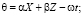
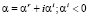 – инкремент; частота
– инкремент; частота 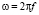 – вещественная величина; волновые числа α, β и частота связаны дисперсионным соотношением α = α(ω, β) линейной теории.
– вещественная величина; волновые числа α, β и частота связаны дисперсионным соотношением α = α(ω, β) линейной теории.
Краевые условия для возмущений – условия прилипания {u, v, w, Θ} = 0 при Y = 0, и условия ограниченности {u, v, w, Θ} > 0 при Y > ∞. Для возмущений первого порядка из так называемой системы Дана – Линя [1] находятся собственные значения α при заданных β, ω и Re, а также собственные амплитудные функции линейных волн (1).
Во втором порядке по ε согласно слабонелинейной теории, используя высшие гармоники (1), определяют амплитуду волны A. В основе резонансной модели лежит процесс попарного взаимодействия волн в поле третьей волны в условиях синхронизации их фаз 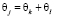 . Для простой трехволновой системы j, k, l волн амплитудные уравнения имеют вид
. Для простой трехволновой системы j, k, l волн амплитудные уравнения имеют вид
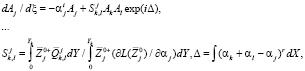
где Δ – коэффициент фазовой синхронизации; 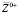 – решения сопряженных к системе Дана – Линя уравнений, Q – нелинейные члены. Начальные значения амплитуд Aj задавались через начальные интенсивности I волновых компонент. Вводились безразмерные частотный параметр F (ω = ReF) и азимутальное волновое число b = 103β/Re. Рассматривались 3D (трехмерные) волны с b ≠ 0.
– решения сопряженных к системе Дана – Линя уравнений, Q – нелинейные члены. Начальные значения амплитуд Aj задавались через начальные интенсивности I волновых компонент. Вводились безразмерные частотный параметр F (ω = ReF) и азимутальное волновое число b = 103β/Re. Рассматривались 3D (трехмерные) волны с b ≠ 0.
Результаты исследования и их обсуждение
Приведем амплитудно-частотные спектры естественных возмущений, полученных в Т-325 экспериментальной группой (А.Д. Косинов, Н.В. Семенов, Ю.Г. Ермолаев). Спектры получены для разных диапазонов частот в широкой полосе Re. Они характеризуются отсутствием ярко выраженных преобладающих компонент, более высокими начальными амплитудами низкочастотных составляющих и преобладающим ростом высокочастотных компонент вниз по потоку. Диапазон применимости слабонелинейного приближения оценивается 600 < Re < 900. При моделировании динамики естественных возмущений были рассмотрены два частотных диапазона. Узкий диапазон частот охватывал полосу (2,5 ≤ f ≤ 30) кГц с шагом Δf = 2,5 кГц. Это соответствовало безразмерным частотным параметрам (0,048 < F < 0,576) 10–4.
Большой диапазон (5 ≤ f ≤ 60) кГц (0,096 < F < 1,152) 10–4 пройден с шагом Δf = 5 кГц.
Второй крайне важной особенностью являлась необходимость синхронизовать в триплетах не только частоты ω, но и азимутальные волновые числа β, при полном отсутствии данных об их реальных значениях. Для синхронизации по β необходимо решать алгебраическую систему на совместность. При этом возникает один свободный азимутальный номер, через который определяются остальные.
Такой определяющей компонентой выбрана волна на частоте f = 20 кГц с азимутальным волновым числом 2b = 0,16. В процессе расчета моделировалось также несколько других вариантов. В представленной таблице показаны комбинации частот и волновых чисел, признанных оптимальными, а на рис. 2 показаны инкременты этих компонент при Re.
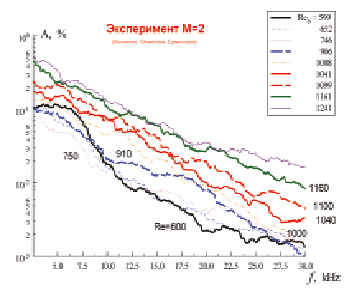
Рис. 1. Эволюция естественных возмущений узкого диапазона частот
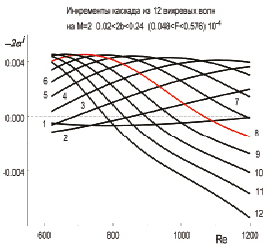
Рис. 2. Примеры выбора несущих азимутальных волновых чисел по значениям инкрементов в широком диапазоне Re
Комбинации частот и волновых чисел, признанных оптимальными
|
104 F |
b |
f кГц |
104 F |
b |
f кГц |
104 F |
b |
f кГц |
|||
|
1 |
0,048 |
0,02 |
2,5 |
2 |
0,096 |
0,04 |
5 |
3 |
0,144 |
0,06 |
7,5 |
|
4 |
0,192 |
0,08 |
10 |
5 |
0,240 |
0,10 |
12,5 |
6 |
0,288 |
0,12 |
15 |
|
7 |
0,336 |
0,14 |
17,5 |
8 |
0,384 |
0,16 |
20 |
9 |
0,432 |
0,18 |
22,5 |
|
10 |
0,480 |
0,20 |
25 |
11 |
0,528 |
0,22 |
27,5 |
12 |
0,576 |
0,24 |
30 |
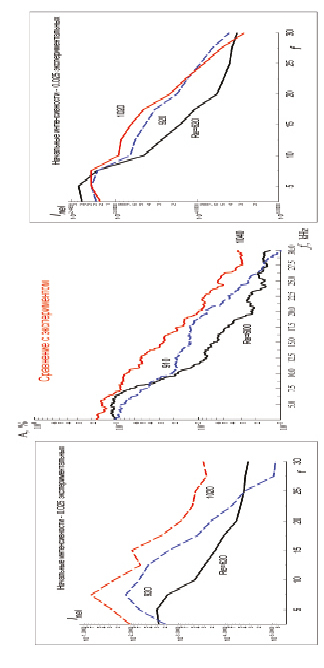
Рис. 3. Результаты моделирования (левая и правая картинки) в сравнении с экспериментом (центр)
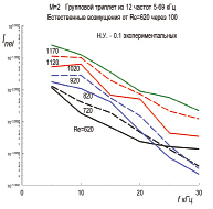
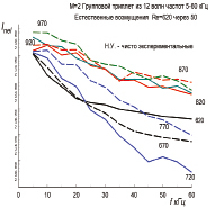
Рис. 4. Расчетные амплитуд естественных возмущений в нелинейной области эволюции на М = 2 для двух диапазонов частот
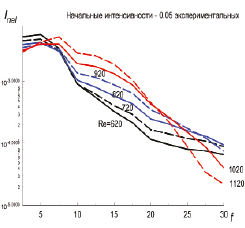
Рис. 5. Расчетные амплитуд естественных возмущений в нелинейной области эволюции на М = 2 при другой несущей частоте
На рис. 3 показано сравнение результатов моделирования и экспериментальных данных в слабонелинейной области для двух вариантов начальных значений интенсивности разных компонент. Результаты оказались в достаточной степени близки друг другу и экспериментальным данным (Косинов, Семенов, Ермолаев), что свидетельствует об адекватности рассматриваемой модели истинному процессу эволюции естественных вихревых возмущений при умеренном сверхзвуковом числе Маха М = 2.
Полные распределения спектров для всех чисел Рейнольдса показаны на рис. 4. Качественное сопоставление этих расчетных спектров можно сделать с данными рис. 1.
На рис. 5 показаны спектры узкого диапазона частот при другом выборе несущей частоты (не 20, а 15 кГц). Как видно из сравнения рис. 3 и 5, такая перенормировка не слишком сказывается на характере продольной динамики спектральных компонент – по-прежнему сильнее растут высокочастотные компоненты и следует ожидать, что при больших Re картины станут адекватны.
Определенные усилия были предприняты для понимания того, каким образом формируется в эксперименте начальный спектр при Re = 600, Для этого расчеты были перенесены в более устойчивую область при низком Re0 ~ 300, и изучалась продольная динамика возмущений при разных начальных интенсивностей в Re0. Было рассмотрено несколько вариантов разных комбинаций:
а. I(F, b, Re0) = const,
в. I(F, b) = exp(-αi Re0),
с. I(F1, b1) = 10k, (F12, b12) = 10k-1,
d. различные комбинации a–c.
Поставленная цель не была достигнута, и вопрос так и остается вопросом, ждущим исследования. В целом можно констатировать, что, хотя рассмотренная модель взаимодействия возмущений в рамках трехволновых резонансных систем является первым шагом в описании динамики естественных волн в слабонелинейной области развития и сильным упрощением реальных нелинейных процессов, она отражает ряд важных особенностей и адекватна истинному процессу. Конечно, в дальнейшем эксперименты должны дать ряд более точных определяющих параметров, которые позволят приблизить моделирование к реальному процессу.
Работа поддержана РФФИ (код проекта № 15-01-00866а).

