Одной из фундаментальных проблем современного материаловедения является получение объемных ультрамелкозернистых (УМЗ) металлов и сплавов, обладающих усовершенствованными свойствами – повышенными прочностью и пластичностью, высокой усталостной прочностью, коррозионной и радиационной стойкостью и др. Металлические материалы с таким высоким уровнем свойств становится возможным получить, применяя методы интенсивной пластической деформации (ИПД). Динамическое канально-угловое прессование (ДКУП) [1] – уникальный метод ИПД, разработанный на базе метода равноканального углового прессования (РКУП) в РФЯЦ ВНИИТФ (г. Снежинск). В отличие от РКУП, метод ДКУП позволяет сохранить высокую пластичность образца после обработки, значительно увеличить скорость пластического деформирования, а также использовать более крупные образцы и сократить общее количество проходов образца через оснастку. Исследования, проводимые в настоящее время, показывают необходимость установления эффективных параметров процесса ДКУП и выявления особенностей ИПД, что становится возможным при применении инструментов численного моделирования [2–7].
Постановка задачи
Процессы, которые рассматриваются в данной работе, имеют нестационарный характер. Также при их описании используется приближение адиабатического процесса применительно к сжимаемой упругопластической среде. Система уравнений, описывающая такое поведение среды, является следствием законов сохранения массы, импульса, энергии:
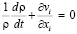 , (1)
, (1)
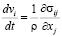 , (2)
, (2)
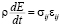 . (3)
. (3)
где ρ – плотность, t – время, vi – компоненты вектора скорости, σij = –Pδij + Sij – компоненты тензора напряжений, E – удельная внутренняя энергия, εij – компоненты тензора скоростей деформаций, P = Рс (ρ/ρc) – среднее давление, δij – символ Кронекера, Sij – компоненты девиатора напряжений, Pc – давление в неповрежденной части вещества.
Во всем диапазоне условий нагружения применяется уравнение состояния, определяющее давление как функцию удельных объема и внутренней энергии:
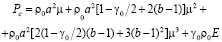 , (4)
, (4)
где μ = V0/(V–Vf), γ0 – коэффициент Грюнайзена, V0 и V – начальный и текущий удельные объемы, a и b – константы адиабаты Гюгонио
us = a+bup,
где us – скорость распространения фронта ударной волны, up – массовая скорость вещества за фронтом ударной волны. Данное уравнение относится к уравнениям состояния типа Ми – Грюнайзена, в котором выделяется «холодная» и «тепловая» части.
Для описания повреждения материала среды используется кинетическая модель разрушения активного типа [8, 9]:
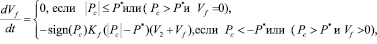 (5)
(5)
где P* = PkV1/(Vf+V1); V1, V2, Pk, Kf – константы (P*>0).
В рамках данной модели степень поврежденности среды характеризуется удельным объемом микроповреждений Vf. Для повреждаемой среды можно определить элементарный объем среды W, который включает объем конденсированной фазы Wc и объем микрополостей (пустот), которые занимают объем Wf. Плотность конденсированной фазы ρc, а плотность пустот полагается равной нулю. Вводится понятие средней плотности повреждаемой среды ρ = ρc (Wc/W). Тогда удельный объем микроповреждений определяется как Vf = Wf/(W ρ). В совокупности такой подход можно определить как модель повреждаемой среды.
Компоненты девиатора напряжений определяются через компоненты тензора скоростей деформаций, при этом используется производная по Яуманну. Пластическое течение описывается с использованием условия текучести Мизеса. Модуль сдвига и динамический предел текучести зависят от температуры и поврежденности материала.
Рассматривается задача взаимодействия титанового образца с пересекающимися каналами. Для системы основных уравнений (1)–(5) в декартовой системе координат ставится задача с начальными и граничными условиями. Начальные условия характеризуются отсутствием внутренних напряжений, а образец движется с начальной скоростью v0. На границах каналов ставится условие жесткой стенки. На тыльной поверхности образца задается постоянная нагрузка P, моделирующая давление пороховых газов. Для решения задачи используется модифицированный метод конечных элементов без глобальной матрицы жесткости, предназначенный для решения задач высокоскоростного нагружения [10].
Численные результаты
Численное моделирование процесса ДКУП в трехмерной постановке выполнено для образцов длиной 65 мм и поперечным сечением 16x16 мм. Каналы оснастки, по которым движется образец, пересекаются под углом 90°; в области внешнего угла пересечения каналов задана наклонная площадкой под углом 45° и высотой 4 мм (рис. 1, а).
В расчетах варьировались величины нагрузки P и начальной скорости образца v0. Анализ результатов серии расчетов позволяет построить диаграмму процесса ДКУП в координатах P – v0 (рис. 1, б) и определить комбинацию их значений, обеспечивающих успешное деформирование образца с полным прохождением по каналам (зона II на рис. 1, б). Диаграмма разделена на следующие зоны:
Зона I: образец останавливается при пересечении каналов оснастки.
Зона II: образец успешно проходит через каналы.
Зона III: образец разрушается во время процесса ДКУП.
Образец успешно проходит через пересекающиеся каналы при достижении минимального значения давления на тыльную поверхность образца, равного 0,6 ГПа. При увеличении начальной скорости образца до 250 м/с возрастает вероятность успешного прохождения процесса ДКУП при значениях P<0,6 ГПа. В правой нижней части диаграммы зоны I и III пересекаются: здесь происходит переход режима процесса ДКУП от остановки образца в области пересечения каналов оснастки к остановке с частичным разрушением образца. С увеличением значений P и v0 были определены верхняя и правая границы зоны II, за которыми прохождение образца по каналам невозможно без накопления критического уровня повреждений или разрушения образца (зона III).
Увеличение значения P при постоянном значении v0 приводит к удлинению образца в направлении продольной оси, также увеличивается средняя скорость движения образца по каналам в течение всего процесса ДКУП. В результате увеличивается скорость пластического деформирования, повышается температура образца. При постоянном значении P увеличение значения v0 также приводит к удлинению образца.
Динамика успешного прохождения образца по пересекающимся каналам представлена на рис. 2.
а б
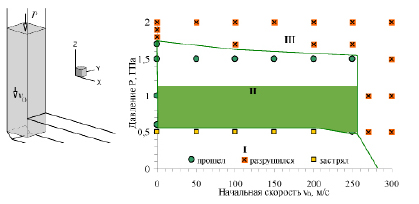
Рис. 1. Начальное положение образца и геометрия пересекающихся каналов (а); P – v0 диаграмма процесса ДКУП титанового образца (б)

Рис. 2. Образец в различные моменты времени процесса: 80, 160 и 240 мкс. P=1 ГПа, v0=100 м/с. Размеры даны в мм
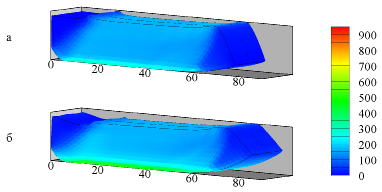
Рис. 3. Распределение удельной энергии сдвиговых деформаций (кДж/кг) в образце: P=1 ГПа, v0=100 м/с, t = 240 мкс (а); P=1,5 ГПа, v0=150 м/с, t = 160 мкс (б). Размеры даны в мм
Исследование полей пластического деформирования в образцах (рис. 3) позволяет сделать вывод о неравномерности процесса деформирования в продольном направлении, это может привести к необходимости повторения процесса ДКУП. В приповерхностных слоях образцов наблюдаются наибольшие значения удельной энергии сдвиговых деформаций ввиду взаимодействия со стенками каналов, при этом в поперечном направлении распределение полей практически полностью идентично.
Заключение
Выполнено численное исследование в трехмерной постановке процессов интенсивного пластического деформирования образцов из титана при ДКУП. Определены значения начальной скорости образца и приложенного к нему давления, обеспечивающие успешное прохождение процесса ДКУП; построена диаграмма процесса в координатах “давление, действующее на тыльный торец образца – начальная скорость образца”. Выделены три области на диаграмме процесса ДКУП, характеризующие поведение образца при различных условиях: область остановки образца при пересечении каналов, область разрушения и область устойчивого прохождения процесса ДКУП. Установлено, что рост средней скорости движения образца по пересекающимся каналам из-за увеличения значений начальной скорости или действующего на него давления приводит к удлинению образца в направлении продольной оси.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 16–43–700774).

