В ферромагнетике с анизотропией типа «легкая ось» нелинейная динамика намагниченности M (r, t) определяется уравнением Ландау–Лифшица [1–2]:
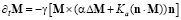 ,
,
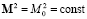 , (1)
, (1)
где 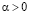 ,
, 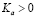 – постоянные обменного взаимодействия и магнитной анизотропии вдоль выделенной оси
– постоянные обменного взаимодействия и магнитной анизотропии вдоль выделенной оси 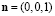 ; γ – магнитомеханическое отношение, t – время. Далее рассматривается квазиодномерный ферромагнетик:
; γ – магнитомеханическое отношение, t – время. Далее рассматривается квазиодномерный ферромагнетик:
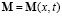 ,
,
где x – пространственная координата.
С помощью масштабных преобразований:
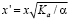 ,
, 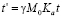 ,
, 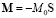
уравнение (1) сводится к виду
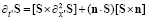 ,
, 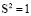 . (2)
. (2)
«Штрихи» над новыми переменными далее опускаем.
Решение уравнения Ландау–Лифшица (2), описывающее простейший прецессирующий солитон на фоне однородного основного состояния легкоосного ферромагнетика, хорошо известно: оно впервые получено непосредственным интегрированием в классической монографии [1]. В книге [2] изложена процедура нахождения точных солитонных решений уравнения (2) на основе метода обратной задачи рассеяния. В основе метода лежит задача сопряжения матричных аналитических функций комплексного переменного.
В данной работе представлены результаты численного эксперимента по возбуждению солитонов в рассматриваемой модели из локализованного начального распределения намагниченности. В рамках формализма обратной задачи аналитически установлена связь физических характеристик солитонов с параметрами исходного распределения, что позволяет генерировать солитоны с требуемыми свойствами.
Основные соотношения. Уравнение (2) равносильно условию совместности вспомогательной линейной системы [2]:
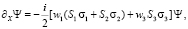 (3)
(3)
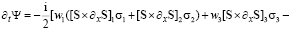
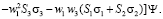
Здесь 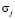 – матрицы Паули, ψ – матрица
– матрицы Паули, ψ – матрица 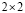 , коэффициенты
, коэффициенты 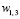 подчинены ограничению:
подчинены ограничению: 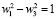 . Удобно использовать параметризацию:
. Удобно использовать параметризацию:
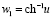 ,
, 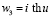 .
.
Нас интересуют решения уравнения Ландау – Лифшица (2) с граничными условиями:
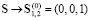 при
при 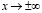 . (4)
. (4)
Условия (4) соответствуют однородному равновесному распределению намагниченности:
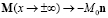 .
.
Им отвечают фундаментальные решения вспомогательной линейной системы (3) с асимптотическим поведением:
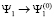 при
при 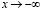 , (5)
, (5)
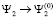 при
при 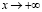 ,
,
где
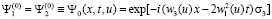 .
.
Множество Г={u : Im u = 0}, mod (2 π i) соответствует непрерывному спектру задачи (3), (5) [2]. На контуре Г фундаментальные решения Ψ1, 2(u) имеют осциллирующее поведение. Они определены одновременно и связаны между собой матрицей перехода:
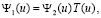
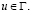
Матрица перехода T(u) унимодулярна (det T = 1) и не зависит от x [2]. Для нее справедливо представление
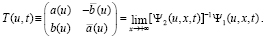 (6)
(6)
Прецессирующий солитон в легкоосном ферромагнетике. Для солитонных решений модели (2) коэффициенты 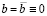 , в то время, как a(u) и
, в то время, как a(u) и 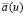 являются мероморфными функциями в u – плоскости. Простейший прецессирующий солитон параметризуется комплексным нулем
являются мероморфными функциями в u – плоскости. Простейший прецессирующий солитон параметризуется комплексным нулем 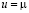 функции
функции 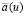 . Соответствующее точное решение можно записать в виде:
. Соответствующее точное решение можно записать в виде:
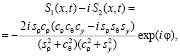
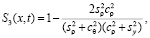 (7)
(7)
где 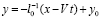 ,
, 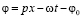 ,
, 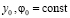 , и для краткости введены обозначения:
, и для краткости введены обозначения:
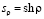 ,
, 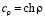 ,
, 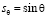 ,
, 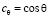 ,
, 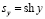 ,
, 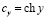 .
.
Ширина области резкого изменения намагниченности солитона l0 , скорость его движения V, волновой вектор p прецессии намагниченности в области локализации солитона, частота ω прецессии в лабораторной системе отсчета и частота Ω в системе отсчета, связанной с солитоном, имеют вид
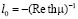 ,
,
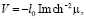
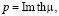
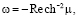
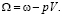
При этом выполняются тождества
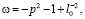
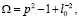
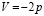 ,
,
позволяющие выразить все физические характеристики солитона через два параметра: p и l0.
Комплексный параметр 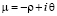 ;
; 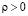 ,
, 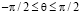 . Наиболее удобны для наблюдения неподвижные солитоны. Солитон (7) неподвижен в двух случаях:
. Наиболее удобны для наблюдения неподвижные солитоны. Солитон (7) неподвижен в двух случаях: 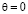 и
и 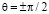 . Случай
. Случай 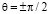 следует считать выделенным. В центре такого солитона намагниченность не прецессирует и направлена в точности вдоль оси
следует считать выделенным. В центре такого солитона намагниченность не прецессирует и направлена в точности вдоль оси 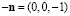 . При этом фазы вращения намагниченности левее и правее центра различаются на π [1, 2]. Это обстоятельство затрудняет его возбуждение.
. При этом фазы вращения намагниченности левее и правее центра различаются на π [1, 2]. Это обстоятельство затрудняет его возбуждение.
При 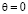 решение (7) принимает вид:
решение (7) принимает вид:
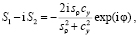
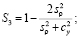
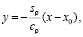
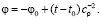 (8)
(8)
На всей протяженности солитона (8) фаза вращения намагниченности одна и та же. Компонента намагниченности S3 в центре солитона не достигает предельных значений ±1: 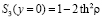 (см. рис. 1).
(см. рис. 1).
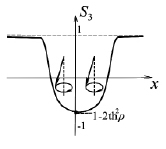
Рис. 1. Компонета S3 и характер прецессии вектора S для неподвижного солитона (8)
Солитон (8) наиболее естественен: его проще всего возбудить в численном эксперименте.
Условие возбуждения неподвижного солитона. Формализм обратной задачи рассеяния позволяет получить условие возбуждения солитона (8). Зададим начальное возмущение в виде ступенчатого распределения намагниченности:
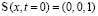 при
при 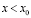 ,
,
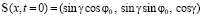
при 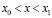 , (9)
, (9)
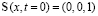 при
при 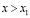 .
.
Подобное распределение можно задать кратковременным включением внешнего магнитного поля вдоль направления 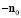 ,
,
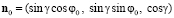 .
.
Параметр γ=const задает амплитуду намагниченности в перемагниченной области шириной 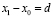 .
.
Следуя той же схеме, что и в работах [3–5], запишем решение первого уравнения (3), соответствующее распределению намагниченности (9). Оно имеет вид
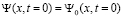 при
при 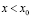 ,
,
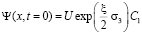
при 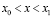 ,
,
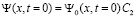 при
при 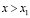 ,
,
где
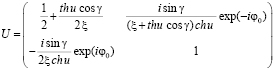 ,
,
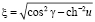 ,
, 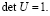
Постоянные матрицы С1, С2 находятся из условия непрерывности функции 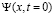 в точках
в точках 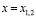 .
.
Начальное возмущение (9) распадается на солитоны, только если элемент 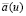 матрицы перехода (6) имеет нули в области своей аналитичности. В этом случае матрица T(u) не зависит от времени [2]. Потому, согласно (6), имеем:
матрицы перехода (6) имеет нули в области своей аналитичности. В этом случае матрица T(u) не зависит от времени [2]. Потому, согласно (6), имеем:
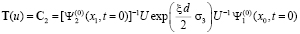 . (10)
. (10)
Из (10) следует, что требование обращения в нуль функции 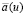 сводится к трансцендентному уравнению
сводится к трансцендентному уравнению
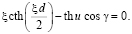 (11)
(11)
Значения d, γ, при которых уравнение (11) имеет вещественный корень 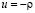 ,
, 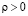 , соответствуют условиям формирования неподвижного солитона (8). Величина ρ определяет физические характеристики такого солитона – его ширину, частоту пульсаций и отклонение намагниченности в его центре от равновесного значения
, соответствуют условиям формирования неподвижного солитона (8). Величина ρ определяет физические характеристики такого солитона – его ширину, частоту пульсаций и отклонение намагниченности в его центре от равновесного значения 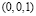 . Выражение (11) дает качественную оценку зависимости ρ от параметров начального возмущения, близкую к результатам численного эксперимента.
. Выражение (11) дает качественную оценку зависимости ρ от параметров начального возмущения, близкую к результатам численного эксперимента.
Связь характеристик солитона с параметрами начального возмущения. Будем понимать под высотой начального импульса (9) h отклонение компоненты 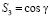 от равновесного значения +1:
от равновесного значения +1:
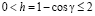 .
.
На рис. 2, рис 3 приведены численные и аналитические зависимости 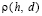 . Жирные точки на рис. соответствуют данным численного эксперимента, сплошные линии построены по формуле (11).
. Жирные точки на рис. соответствуют данным численного эксперимента, сплошные линии построены по формуле (11).
Результаты численного счета говорят о том, что с изменением ширины d начального импульса при его фиксированной высоте h солитон (8) рождается из распределения (9) пороговым образом. Локализованное возмущение малой ширины не порождает солитона: при 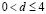 начальный импульс (8) произвольной высоты расплывается на диспергирующие спиновые волны. С ростом ширины возмущения (в интервале значений
начальный импульс (8) произвольной высоты расплывается на диспергирующие спиновые волны. С ростом ширины возмущения (в интервале значений 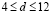 ) из начального импульса (9) формируется неподвижный солитон (8) с центром в его середине. Высота такого импульса
) из начального импульса (9) формируется неподвижный солитон (8) с центром в его середине. Высота такого импульса 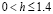 может быть сколь угодно малой: в пределах погрешности счета не удалось обнаружить ее минимальное значение.
может быть сколь угодно малой: в пределах погрешности счета не удалось обнаружить ее минимальное значение.
Изображенная на рис. 2 зависимость ρ от высоты 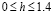 начального возмущения при его фиксированной ширине
начального возмущения при его фиксированной ширине 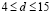 почти линейна. При фиксированной высоте h величина ρ монотонно возрастает с ростом ширины начальной ступеньки, меняясь в пределах:
почти линейна. При фиксированной высоте h величина ρ монотонно возрастает с ростом ширины начальной ступеньки, меняясь в пределах:
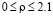 .
.
Задание начального импульса небольшой высоты (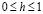 ) и значительной ширины (
) и значительной ширины (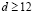 ) ведет к интересному результату. Тогда возмущение (9) сначала сужается до значения
) ведет к интересному результату. Тогда возмущение (9) сначала сужается до значения 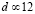 , сбрасывая излишек энергии в виде диспергирующих волн, а затем из него также формируется неподвижный солитон (8). В соответствии с этим, при больших
, сбрасывая излишек энергии в виде диспергирующих волн, а затем из него также формируется неподвижный солитон (8). В соответствии с этим, при больших 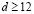 зависимость
зависимость
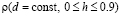
на рис. 3 становится пологой.
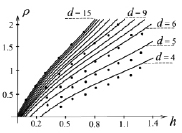
Рис. 2. Зависимость 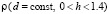 при значениях
при значениях 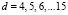
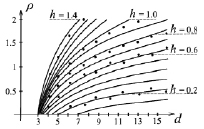
Рис. 3. Зависимость 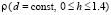 при значениях
при значениях 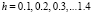
Заключение
Численное моделирование показывает, что при условии 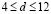 значение
значение 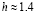
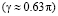 является порогом, по превышении которого (при
является порогом, по превышении которого (при 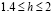 ) начальное возмущение (9) порождает два одинаковых солитона (7), движущихся в противоположных направлениях. С дальнейшим увеличением ширины импульса d значение его высоты h, необходимое для формирования двух солитонных состояний, несколько снижается: так при
) начальное возмущение (9) порождает два одинаковых солитона (7), движущихся в противоположных направлениях. С дальнейшим увеличением ширины импульса d значение его высоты h, необходимое для формирования двух солитонных состояний, несколько снижается: так при 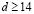 два солитона формируются из начального возмущения высотой
два солитона формируются из начального возмущения высотой 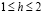 , что соответствует значениям
, что соответствует значениям 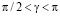 .
.
Уравнение (11) не позволяет установить пороговое значение h , при котором рождаются два солитона (7). Вместе с тем, рис. 2, 3 убеждают нас, что полученная оценка (11) зависимости параметра ρ солитона (8) от высоты и ширины начального импульса находится в хорошем согласии с численным экспериментом и может быть использована для генерации неподвижных солитонов с требуемыми характеристиками.
В заключение заметим, что при формировании прецессирующих солитонов в легкоосном ферромагнетике энергия начального возмущения (9) перераспределяется между компонентами намагниченности. Это приводит к тому, что ни ширина d, ни проекция 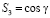 начального возмущения в области
начального возмущения в области 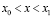 не совпадают с таковыми у результирующего солитона.
не совпадают с таковыми у результирующего солитона.
Авторы выражают благодарность В.В. Киселеву за обсуждение результатов работы и полезные замечания.
Работа выполнена в рамках проекта УрО РАН №15–8–2–7 «Локализованные структуры, солитоны и их возбуждение в конденсированных средах».

