В условиях современных лесозаготовок на трелевке древесины широко используются форвардеры с колесным или гусеничным движителем, предназначенные для сбора и транспортировки сортиментов в пределах лесосеки [1–3]. Форвардер, загруженный древесиной, имеет значительную массу, что вызывает уплотнение и разрушение лесной подстилки, а также является причиной потери несущей способности почвогрунтов. Для обеспечения долгосрочного сохранения несущей способности грунта в работах [4–6] предлагаются технические решения, направленные на увеличение проходимости лесозаготовительных машин, в частности путем укрепления проезжей части транспортных путей лесосечными отходами и определение предельного количества проходов лесозаготовительной техники по волоку. При этом следует учитывать, что удельное давление на грунт трелевочных машин с гусеничным движителем меньше в 3,5–6 раз, чем с колесным [2, 3]. В тяжелых условиях эксплуатации колесные форвардеры сталкиваются с проблемой недостаточной проходимости при движении по почвогрунтам 3–4 категории. В этих условиях их оснащают съемными гусеницами и цепями для повышения проходимости и предотвращения буксования и застревания, которые ведут к интенсивному колееобразованию, эрозии почвенного покрова и разрушению лесной подстилки.
Один из частных способов уменьшения разрушения лесной подстилки – снижение давления от движителя лесозаготовительной техники. В связи с этим в качестве движителей используют шины широких профилей или гусеницы [7]. В данное время наибольшее распространение получила колесная техника, которая используется в сочетании с гусеницами и цепями противоскольжения [8]. Последние позволяют увеличить только сцепление с грунтом, в то время как гусеницы противоскольжения за счет грунтозацепов обеспечивают высокий коэффициент сцепления и снижение удельного давления на грунт.
В статье рассматривается конструкция цепей противоскольжения, используемая на форвардерах. Расчетная модель (рис. 1, а), включает в себя: 1 – шина 750/55–26,5; 2 – диск; 3 – трак; 4 – грунт.
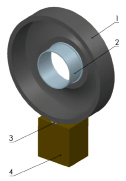

а б
Рис. 1. 3Д-модели: а – расчетная сборка; б – трак гусеницы
Так как на исследуемой гусенице период расположения траков составил 225 мм, в контакте между шиной и почвой участвует только один элемент трака. В контактной зоне трак имеет форму параллелепипеда (рис. 1, б). В данной расчетной модели, шина не имеет протектора, поэтому считаем, что трак контактирует с поверхностью шины равномерно.
Материалы контактирующих элементов (шина, трак, почва) характеризуются в расчете как упругие, линейные и изотропные. Их механические свойства представлены в таблице.
Механические свойства контактирующих элементов
|
Наименование элемента |
Механические свойства |
||
|
Модуль упругости, Е, Н/м2 |
Коэффициент Пуассона |
Предел текучести, МПа |
|
|
Шина [9] |
4·108 |
0,49 |
– |
|
Трак |
2,1·1011 |
0,28 |
620 |
|
Почва [10] |
4·107 |
0,35 |
– |
Внутренние поверхности шины и часть диска, находящаяся внутри нее, нагружены давлением 550 кПа [11]. Коэффициент трения скольжения между шиной и траком и между траком и почвой принят равным усредненному значению – 0,5 [12]. Нижняя часть элемента грунта закреплена от перемещений во всех направлениях.
Дальнейшие расчеты рассматриваются в статической постановке, с учетом того, что колесо воспринимает нагрузку от веса, приходящегося на одно колесо тележки форвардера. Нагрузка от силы тяжести, приходящейся на колесо, распределена неравномерно и имеет синусоидальное распределение нагрузки на поверхности диска:
F(a) = mн•g•sin(a),
где mн = 6000 кг – масса, приходящаяся на каждое колесо форвардера, g = 9,81 м/с2 – ускорение свободного падения, a = 0 °…180 ° – угол изменения охвата диска (рис. 2).
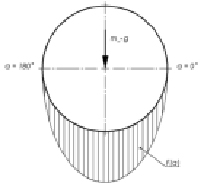
Рис. 2. Распределенная нагрузка на диск колеса
Исследованы три случая нагружения: 1 – продольные плоскости симметрии трака и колеса совпадают (рис. 3, а), 2 – продольная плоскость симметрии трака смещена на четверть его ширины от продольной плоскости симметрии колеса (рис. 3, б); 3 – продольная плоскость симметрии трака смещена на половину его ширины от продольной плоскости симметрии колеса (рис. 3, в).



а б в
Рис. 3. Расчетные случаи нагружения: а – без смещения, б – смещение на четверть ширины трака; в – смещение на половину ширины трака

Рис. 4. Конечно-элементная модель
Конечно-элементная модель (рис. 4) содержит 36714 элемента и 60265 узлов. В местах контакта шины, трака и почвы, для улучшения точности расчета, элементы сетки измельчены.
Получены расчетные эпюры контактного давления на поверхность грунта (рис. 5).
Во время движения форвардера часть траков гусеницы, находящихся в области контакта, расположены как под поверхностью колеса, так и на поверхности грунта. Можем принять условие, что расстояние между траками по окружности (трак на колесе) равно расстоянию между ними по горизонтали. Для уменьшения контактного давления уменьшено расстояние между траками с 225 мм до 103 мм, что позволило перераспределить нагрузку между траками. Расстояние 103 мм обеспечивает движение гусеницы на всех участках, таким образом, чтобы обеспечивалось минимальное расстояние между траками с исключением их пересечения в динамике. Соединения между траками моделируется созданием жестких звеньев между торцевыми поверхностями, с помощью встроенной функции.



а б в
Рис. 5. Распределения контактного давления на поверхности грунта: а – для первого случая нагружения; б – второго; в – третьего
а б в
Рис. 6. Расчетные случаи нагружения: а – без смещения, б – смещение на четверть ширины трака; в – смещение на половину ширины трака


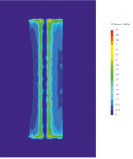
а б в
Рис. 7. Распределения контактного давления на поверхности грунта: а – для первого случая нагружения; б – второго; в – третьего
Второй случай нагружения (рис. 6) аналогичен первому, за исключением того, что траки расположены с периодом 103 мм, обеспечивающим распределение контактного давления на поверхности грунта между тремя (рис. 7, а–б) и двумя траками (рис. 7, в).
В обоих расчетных случаях нагружения, контактное давление передается на почву крайними контурами траков, в центральной же части оно стремится к наименьшему значению. За счет уменьшения расстояния между траками достигается снижение максимального контактного давления: для первой схемы нагружения – на 8 %; для второй схемы нагружения – на 30 %; и для третьей – на 44,5 %. Если же не учитывать точечное возникновение максимального давления (вызванное геометрическими параметрами модели трака), а судить по среднему напряжению контура траков, образующих некий периметр прямоугольной формы, то получатся следующие значения процентного снижения контактного давления. Для первой схемы нагружения – на 8 %; для второй схемы нагружения – на 22 %; и для третьей – на 38 %.
По результатам расчета можно сделать ряд выводов. Во-первых, увеличение числа траков в области контакта с грунтом снижает давление на почву, за счет увеличения общей площади контактируемых элементов. С другой стороны – такое решение приводит к увеличению массы гусениц (из-за большего количества траков), а также – к увеличению крутящего момента, который необходимо подвести к колесам (за счет увеличения площади трения). Во-вторых, по предлагаемой методике возможно оценить давление на грунт, в зависимости от его упругих свойств, и на основании расчетов принимать конструкторские решения по увеличению (уменьшению) количества траков и (или) изменению их геометрии. В-третьих, по полученным эпюрам распределения контактного давления можно заключить, что центральная часть трака гусеницы передает давление на почву в разы меньше, чем часть, расположенная в зоне периметра контакта. Поэтому из соображений уменьшения массы трака в дальнейшем следует рассмотреть исключение передачи давления центральной частью трака, за счет изменения его геометрии.

