Постановка задачи
Для разработки и проектирования современных каналов связи ставятся задачи гармонического анализа сигналов и расчет амплитудно-частотных характеристик элементов телекоммуникаций, таких как фильтры, усилители и др. [1]. То есть проводят гармонический анализ как сигналов, так и элементов телекоммуникаций.
В основе гармонического или спектрального анализа лежит разложение в ряды функций, описывающих различные физические процессы. Гармонический анализ используется в радиотехнических, радиофизических и других задачах при моделировании процессов распространения радиоволн через различные среды, прохождения сигналов через радиотехнические цепи и многих других волновых задач [1]. Для гармонического анализа периодических сигналов f(x) используется разложение в ряды по ортогональным функциям φi(x). Систем ортогональных функций множество. Наиболее часто встречаются системы тригонометрических функций 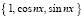 , кроме того, в системах цифровой обработки сигналов часто применяются дискретные функции Уолша Wi(t) [1, 2]. При разложении функции в функциональный ряд
, кроме того, в системах цифровой обработки сигналов часто применяются дискретные функции Уолша Wi(t) [1, 2]. При разложении функции в функциональный ряд
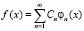 (1)
(1)
необходимо определить коэффициенты ряда разложения Ci. Эта операция сопряжена с вычислением определенного интеграла вида
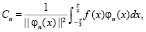 (2)
(2)
где T – период сигнала, 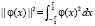 – квадрат нормы для φ(x).
– квадрат нормы для φ(x).
В настоящее время указанные преобразования определены только для сигналов, представленных в позиционной системе счисления (ПСС) [3]. В ПСС числа представляются последовательностью цифр на соответствующих позициях. В настоящее время все больший интерес проявляется к параллельным сигналам, представленным в непозиционной системе счисления [3, 4], такой как система остаточных классов (СОК). Преимущество СОК заключается в возможности выполнения операций сложения и умножения параллельно, т.е. без переносов в разрядах числа. При этом числа представляются параллельным набором остатков от деления по L взаимно простым основаниям pi, где 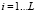 [4, 5]. Применение параллельной передачи и обработки параллельных сигналов многократно повышает производительность, пропускную способность и другие характеристики средств телекоммуникаций [1, 5]. В основе цифровых систем телекоммуникаций лежит обработка дискретных сигналов, когда f(t) представляется последовательностью k импульсов с амплитудой fk и длительностью τk. Очевидно, что для параллельной передачи и обработки данных необходимо проводить тот же гармонический анализ элементов телекоммуникаций. Если при этом в канале связи используется параллельный сигнал, представленный в формате СОК, то необходимо разработать математический аппарат такого анализа в СОК.
[4, 5]. Применение параллельной передачи и обработки параллельных сигналов многократно повышает производительность, пропускную способность и другие характеристики средств телекоммуникаций [1, 5]. В основе цифровых систем телекоммуникаций лежит обработка дискретных сигналов, когда f(t) представляется последовательностью k импульсов с амплитудой fk и длительностью τk. Очевидно, что для параллельной передачи и обработки данных необходимо проводить тот же гармонический анализ элементов телекоммуникаций. Если при этом в канале связи используется параллельный сигнал, представленный в формате СОК, то необходимо разработать математический аппарат такого анализа в СОК.
Таким образом, целью данной статьи является определение операций разложения дискретных сигналов в СОК в ряды Фурье и Уолша.
Разложение в ряд Фурье дискретного сигнала в СОК
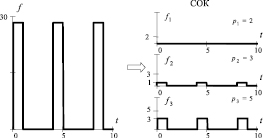
Рис. 1. Преобразование сигнала из ПСС в СОК
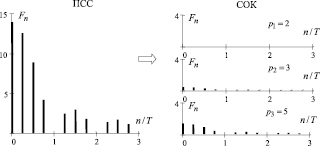
Рис. 2. Преобразование спектра Фурье
В дальнейшем в качестве сигнала рассмотрим произвольный k импульс с амплитудой f и 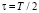 (рис. 1, слева). Дискретный сигнал в системе СОК (рис. 1, справа) будет представлен набором сигналов
(рис. 1, слева). Дискретный сигнал в системе СОК (рис. 1, справа) будет представлен набором сигналов
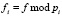 , (3)
, (3)
каждый из которых можно разложить в ряд Фурье, так как модульная операция не нарушает условий Дирихле. Для тригонометрических базисных функций выражение (1) определяется для четных и нечетных функций как [1]
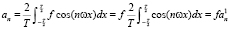 ,
,
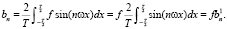 (4)
(4)
где 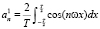 и
и 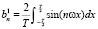 – коэффициенты ряда для элементарного единичного импульса. Учитывая правила модулярного интегрирования [6], подстановка (3) в (4) позволяет получить коэффициенты ряда в виде
– коэффициенты ряда для элементарного единичного импульса. Учитывая правила модулярного интегрирования [6], подстановка (3) в (4) позволяет получить коэффициенты ряда в виде
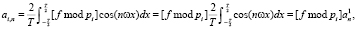
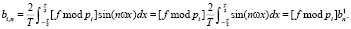 (5)
(5)
Таким образом, разложение в ряд Фурье для дискретного сигнала в СОК будет определяться не множеством коэффициентов, а матрицами коэффициентов 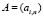 и
и 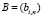 размерностью (L×N), где N – число коэффициентов ряда. Из (3) выразим
размерностью (L×N), где N – число коэффициентов ряда. Из (3) выразим 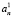 и
и 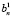 в виде
в виде
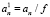 ,
, 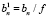 . (6)
. (6)
Подстановка (6) в (5) позволяет получить соотношение между коэффициентами ряда Фурье дискретного сигнала в ПСС с коэффициентами ряда того же сигнала в СОК в виде
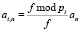 ,
, 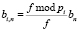 . (7)
. (7)
Таким образом, с учетом (7) разложение в ряд Фурье (1) для сигнала в СОК можно записать в виде
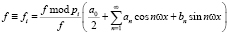 . (8)
. (8)
Представим последовательность импульсов длительностью τ = 1 с периодом T = 4 и амплитудой A = 28 в СОК по основаниям pi = 2, 3, 5 (рис. 1).
Спектральное представление соответствующих последовательностей в ПСС и в СОК будет иметь вид как на рис. 2. При этом отношение 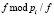 примет для pi = 2, 3, 5 значения 0,
примет для pi = 2, 3, 5 значения 0, 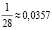 и
и 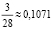 .
.
Для непериодического сигнала f представляется не в виде ряда Фурье (8), а в виде преобразования Фурье
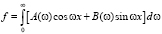 , (9)
, (9)
где
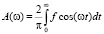
и
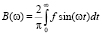
прямое косинус и синус преобразования Фурье (9) дискретного сигнала f, определяющие его амплитудный спектр 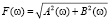 . Преобразование Фурье является предельным переходом ряда Фурье для
. Преобразование Фурье является предельным переходом ряда Фурье для 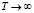 , поэтому аналогично (1–8) определим преобразование Фурье сигнала в СОК в виде
, поэтому аналогично (1–8) определим преобразование Фурье сигнала в СОК в виде 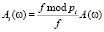 и
и 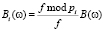 , а его амплитудный спектр как
, а его амплитудный спектр как
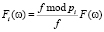 . (10)
. (10)
Заметим, что фазовые спектры дискретного сигнала в СОК для каждого основания pi будут одинаковыми и равны фазовому спектру 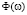 исходного дискретного сигнала в ПСС
исходного дискретного сигнала в ПСС
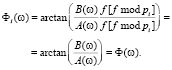 (11)
(11)
Легко заметить, что фазовые спектры дискретного сигнала в СОК будут равны фазовому спектру исходного дискретного сигнала в ПСС и при преобразовании не изменятся.
Используя амплитудно- и фазо-частотные характеристики (10, 11) параллельных подканалов и статистические характеристики вычетов [7] передаваемых данных, в дальнейшем можно вычислять показатели качества и характеристики общего параллельного канала при передаче данных в СОК.
Разложение в ряд Уолша дискретного сигнала в СОК
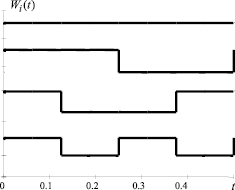
Рис. 3. Функции Уолша
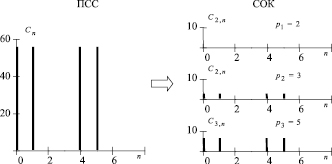
Рис. 4. Преобразование спектра Уолша
Согласно выражению (10) спектры сигналов в СОК и в ПСС не могут быть сравнимы, так как операция сравнения определена только для целочисленных функций. Однако во многих задачах цифровой обработки дискретных сигналов для гармонического анализа используются ортогональные функции Уолша Wi(t), определяемые рекуррентными формулами. Данные функции являются дискретным аналогом функций косинуса и синуса (рис. 3), однако имеют целочисленные значения. Подобные функции используются в вычислительной и цифровой технике. Фактически функции Уолша представляют собой меандр с периодом кратным частотам ряда Фурье. На рис. 3 представлен пример четырех таких функций. Третья, четвертая и последующая функции формируются путем уменьшения периода и соблюдения ортогональности со второй функцией. Первая является константой и отвечает за постоянный компонент исследуемого процесса.
При разложении дискретного сигнала в базисе Уолша сигнал представляется дискретными отсчетами 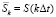 в виде среднего значения сигнала на интервале дискретизации, где Δt – интервал дискретизации,
в виде среднего значения сигнала на интервале дискретизации, где Δt – интервал дискретизации, 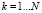 ,
, 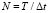 – число интервалов дискретизации. Для дискретного сигнала среднее значение на интервале дискретизации равно значению сигнала
– число интервалов дискретизации. Для дискретного сигнала среднее значение на интервале дискретизации равно значению сигнала 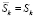 . Значения спектральных составляющих определяются как сумма произведений дискретных значений сигнала на дискретные значения функции Уолша:
. Значения спектральных составляющих определяются как сумма произведений дискретных значений сигнала на дискретные значения функции Уолша:
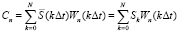 , (12)
, (12)
Так, для дискретного сигнала (рис. 1) ненормированные нечетные коэффициенты ряда Уолша будут иметь значения 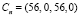 . Рассмотрим разложение в ряд для того же сигнала в СОК:
. Рассмотрим разложение в ряд для того же сигнала в СОК:
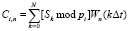 . (13)
. (13)
Согласно теории сравнений [5], если 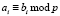 , то справедливы сравнения
, то справедливы сравнения 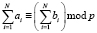 и
и 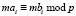 , где m – целое. Так как функции Уолша принимают только целые значения, то справедливо
, где m – целое. Так как функции Уолша принимают только целые значения, то справедливо
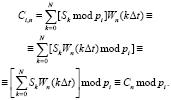 (14)
(14)
Таким образом, спектр Уолша 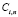 дискретного сигнала в СОК по основаниям pi определяется представлением спектра исходного дискретного сигнала в ПСС по тем же основаниям в СОК.
дискретного сигнала в СОК по основаниям pi определяется представлением спектра исходного дискретного сигнала в ПСС по тем же основаниям в СОК.
Действительно, для сигнала в СОК (рис. 1) нечетные коэффициенты ряда Уолша будут иметь 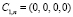 ,
, 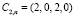 и
и 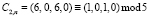 (рис. 4).
(рис. 4).
Полученные данные в совокупности с методикой расчета вероятностей вычетов [7] в параллельном формате сигнала в СОК необходимо использовать для расчета полос пропускания, скоростей передачи данных, распределения спектральных полос по подканалам в общем параллельном канале связи.
Выводы
Цель статьи достигнута, получены необходимые аналитические выражения для выполнения операций разложения дискретных сигналов в ряды Фурье и Уолша. Кроме того, можно сделать выводы:
1. Выражения (8) и (10) определяют взаимосвязь между Фурье спектрами дискретных сигналов в СОК и ПСС.
2. Фазовые спектры дискретного сигнала в СОК будут равны фазовому спектру исходного дискретного сигнала в ПСС.
3. Спектр Уолша дискретного сигнала в СОК сравним со спектром того же дискретного сигнала в ПСС.

