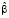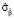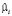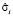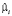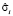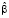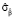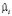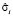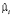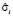Учитывая изношенность основных фондов предприятий туристической инфраструктуры в России (свыше 70 %), развитие сферы туризма невозможно без привлечения инвестиций в развитие экономики, в том числе и на уровне регионов [1]. Строительство новых или реконструкция старых объектов туристской рекреации региона требуют прогнозной оценки эффективности инвестиций в сферу туризма. Данный прогноз может быть получен в рамках эконометрического моделирования с привлечением аппарата систем внешне не связанных уравнений и моделей для панельных данных [2–4].
Статистические данные
Использованы данные Российского статистического ежегодника 2016 г. [5]. Показатели приведены в разрезе Центрального федерального округа Российской Федерации за 2009–2015 гг.: по объему инвестиций в основной капитал, направленных на развитие коллективных средств размещения (гостиниц, прочих мест для временного проживания) (в млн рублей); по численности лиц, размещённых в гостиницах и аналогичных средствах размещения (в тыс. человек). По каждой области имеется информация за 6 лет, число областей – 18. Названия областей приведены в табл. 1.
Таблица 1
Названия областей
|
Номер области i |
Название области |
Номер области i |
Название области |
|
1 |
Белгородская |
10 |
Московская |
|
2 |
Брянская |
11 |
Орловская |
|
3 |
Владимирская |
12 |
Рязанская |
|
4 |
Воронежская |
13 |
Смоленская |
|
5 |
Ивановская |
14 |
Тамбовская |
|
6 |
Калужская |
15 |
Тверская |
|
7 |
Костромская |
16 |
Тульская |
|
8 |
Курская |
17 |
Ярославская |
|
9 |
Липецкая |
18 |
г. Москва |
Выбор эконометрического инструментария и анализ результатов
Выборочные данные состоят из наблюдений за большим числом однотипных объектов (18 областей) в течение небольшого периода времени (6 лет). Поэтому в качестве инструмента выбран аппарат систем внешне не связанных уравнений (Seemingly Unrelated Regression, SUR) и модели для панельных данных, позволяющие выполнять оценивание при небольшом объеме выборки для отдельных экономических единиц [6–8].
Система внешне не связанных уравнений отличается от системы одновременных уравнений тем, что в ней переменные отдельных уравнений независимы, но их случайные возмущения коррелированы, поскольку моделируемые каждым отдельным уравнением объекты функционируют в «одной экономической среде».
Уравнения системы можно рассматривать по отдельности для каждого экономического объекта (области), и оценивать обычным методом наименьших квадратов, однако если возмущения уравнений для отдельных областей коррелированы, то эта дополнительная информация дает возможность повысить эффективность оценок параметров в рамках системы внешне не связанных уравнений. Спецификация модели SUR имеет вид
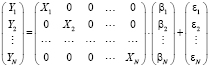 , (1)
, (1)
где 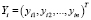 – вектор-столбец значений эндогенной переменной для i-го объекта,
– вектор-столбец значений эндогенной переменной для i-го объекта, 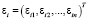 – вектор-столбец возмущений для i-го уравнения, Xi – матрица регрессоров для i-го объекта,
– вектор-столбец возмущений для i-го уравнения, Xi – матрица регрессоров для i-го объекта, 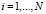 ,
, 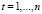 , N – число объектов (число уравнений), n – число наблюдений. Систему (1) можно записать в матричном виде
, N – число объектов (число уравнений), n – число наблюдений. Систему (1) можно записать в матричном виде
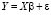 , (2)
, (2)
где 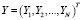 – (nN×1) вектор-столбец значений эндогенных переменных,
– (nN×1) вектор-столбец значений эндогенных переменных, 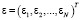 – (nN×1) вектор-столбец возмущений,
– (nN×1) вектор-столбец возмущений,
 – матрица регрессоров,
– матрица регрессоров,
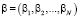 – (kN×1) вектор-столбец оценок параметров.
– (kN×1) вектор-столбец оценок параметров.
Относительно объединённого вектора случайных возмущений системы принимаются предпосылки: E(ε) = 0;
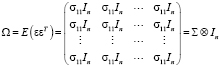 (3)
(3)
– автоковариационная матрица вектора возмущений, In – единичная матрица размером n×n, 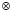 – символ кронекерова перемножения матриц,
– символ кронекерова перемножения матриц,
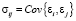 – ковариация между возмущениями i-го и j-го уравнений, Σ – ковариационная матрица с элементами σij,
– ковариация между возмущениями i-го и j-го уравнений, Σ – ковариационная матрица с элементами σij, 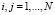 .
.
Для оценки параметров модели (2) с числовыми характеристиками (3) применяется обобщенный метод наименьших квадратов (ОМНК)
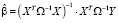 . (4)
. (4)
Для вычисления ОМНК-оценок (4) необходимо оценить автоковариационную матрицу возмущений Ω (3). В эконометрических пакетах прикладных программ для этой цели используется доступный вариант SUR – FGLS (The general feasible generalized least-squares method), в котором МНК-оценки параметров отдельных уравнений, входящих в систему, служат основой для вычисления элементов матрицы Σ [9]:
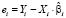 ,
, 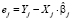 ,
,
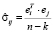 ,
, 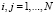 , (5)
, (5)
и далее, по формуле (3), вычисляются элементы матрицы 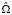 . В случае если уравнения системы (2) действительно не связаны друг с другом, σij = 0 при i ≠ j, оценки параметров (4) совпадают с МНК-оценками, полученными для каждого отдельного уравнения. Ниже приведен протокол оцененной модели SUR, полученный в программной среде R (при помощи функции systemfit , библиотеки systemfit):
. В случае если уравнения системы (2) действительно не связаны друг с другом, σij = 0 при i ≠ j, оценки параметров (4) совпадают с МНК-оценками, полученными для каждого отдельного уравнения. Ниже приведен протокол оцененной модели SUR, полученный в программной среде R (при помощи функции systemfit , библиотеки systemfit):
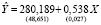 , R2 = 0,791,
, R2 = 0,791,
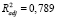 , F = 400.
, F = 400.
Данный результат совпадает с оценками модели Pooled (объединенной) для панельных данных (функция plm, библиотеки plm в программной среде R).
Основными регрессионными моделями, применяемыми к панельным данным, являются:
- объединённая модель (pooled model, Pool), предполагающая, что у экономических объектов нет индивидуальных различий
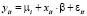 ,
, 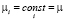 , (6)
, (6)
где yit – зависимая переменная,
xit – вектор-строка регрессоров (размерностью k),
εit – случайное возмущение; i = 1, …, n, t = 1, …, T,
n – число объектов (панелей), T – число наблюдений в рамках одной панели,
μ = const – постоянное для всех объектов значение свободного члена – параметр «местоположения», β = βpool – вектор параметров «влияния», постоянный для всех объектов (панелей),
- модель с фиксированным эффектом (fixed effect model, FE), базирующаяся на «уникальности» экономических объектов
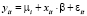 ,
, 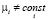 , (7)
, (7)
μi – параметр местоположения i-го объекта, 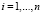 ,
,
- модель со случайным эффектом (random effect model, RE), учитывающая «случайность» попадания объекта в панель в результате выборки из большой совокупности:
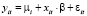 ,
, 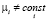 ,
, 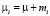 ,
,
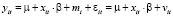 , (8)
, (8)
где mi – независящая от времени специфическая составляющая ошибки.
Для оценки регрессионных моделей для панельных данных в программной среде R используется функция plm (библиотеки plm), одним из параметров которой является название модели (model) из списка основных: model="pooling" (объединенная модель), model="within" (модель с фиксированными эффектами), model="random" (модель со случайными эффектами).
Выбор одной модели из списка основных выполняется на основании формальных тестов. Так, например, при тестировании объединённой модели против модели с фиксированными эффектами, в качестве нулевой гипотезы выбирается 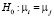 . Эта гипотеза проверяется при помощи F-теста
. Эта гипотеза проверяется при помощи F-теста
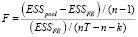 ,
,
где используются следующие обозначения:
k – число параметров влияния, ESSpool – сумма квадратов остатков объединённой модели, ESSFE – сумма квадратов остатков модели с фиксированными эффектами. Если F > Fα, при определенном уровне значимости α, то гипотеза 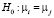 отвергается и наиболее адекватной признается модель с фиксированными эффектами, в противном случае нулевая гипотеза принимается, и лучшее соответствие результатам наблюдений должна обеспечить объединенная модель.
отвергается и наиболее адекватной признается модель с фиксированными эффектами, в противном случае нулевая гипотеза принимается, и лучшее соответствие результатам наблюдений должна обеспечить объединенная модель.
При тестировании объединённой модели против модели со случайными эффектами нулевой гипотезой является 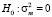 . Для проверки этой гипотезы используется тест множителей Лагранжа, который базируется на статистике
. Для проверки этой гипотезы используется тест множителей Лагранжа, который базируется на статистике
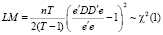 ,
,
где e – вектор-столбец остатков модели в объединённой регрессии, D – матрица фиктивных переменных. Если 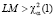 , то нулевая гипотеза отвергается при уровне значимости α, и наиболее адекватной признается модель со случайными эффектами.
, то нулевая гипотеза отвергается при уровне значимости α, и наиболее адекватной признается модель со случайными эффектами.
Тестирование модели со случайными эффектами против модели с фиксированными эффектами основано на проверке справедливости нулевой гипотезы 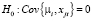 , против альтернативной
, против альтернативной 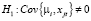 . Статистика теста, статистика Хаусмана, определяется по правилу
. Статистика теста, статистика Хаусмана, определяется по правилу
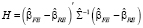 ,
,
где 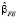 – оценка параметров модели с фиксированными эффектами,
– оценка параметров модели с фиксированными эффектами, 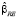 – оценка параметров модели со случайными эффектами,
– оценка параметров модели со случайными эффектами, 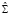 – оценка автоковариационной матрицы вектора
– оценка автоковариационной матрицы вектора 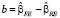 .
.
Тестирование характера эффектов, выполненное в программной среде R (при помощи функций: pFtest() – модель Pooled против модели FE, plmtest() – модель Pooled против модели RE, phtest() – модель RE против модели FE), показало значимость модели (7) с фиксированными эффектами.
В табл. 2 и 3 приводятся оценки параметров положения и влияния, полученные в рамках модели FE для панельных данных при помощи функции plm [10].
Таблица 2
Оценка параметра (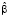 ) влияния в модели FE
) влияния в модели FE
|
|
|
t-статистика |
|
0,1396 |
0,0126 |
11,034 |
R2 = 0,59. F-statistic: 121,76 on 1 and 89 DF, p-value: < 2.22e-16
Таблица 3
Оценки параметров местоположения (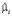 ) в модели FE
) в модели FE
|
Номер области i |
|
|
t |
Номер области i |
|
|
t |
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
1 |
171,586 |
48,806 |
3,5156 |
10 |
2192,401 |
57,717 |
37,9851 |
|
2 |
125,271 |
48,805 |
2,5668 |
11 |
97,166 |
48,818 |
1,9904 |
|
3 |
425,660 |
48,813 |
8,718 |
12 |
218,454 |
48,805 |
4,4760 |
|
4 |
298,024 |
48,805 |
6,1064 |
13 |
185,358 |
48,808 |
3,7977 |
|
5 |
194,090 |
48,805 |
3,9769 |
14 |
109,107 |
48,805 |
2,2355 |
|
6 |
300,331 |
49,006 |
6,1285 |
15 |
329,569 |
48,862 |
6,7407 |
|
7 |
184,887 |
48,805 |
3,7883 |
16 |
216,625 |
48,805 |
4,4386 |
|
8 |
136,170 |
48,805 |
2,7901 |
17 |
364,967 |
49,214 |
7,4159 |
|
9 |
134,247 |
48,808 |
2,7505 |
18 |
3340,442 |
91,690 |
36,4317 |
Функция pggls, для обобщенного FGLS метода, позволяет построить аналоги моделей панельных данных со случайными (random effect model, RE) и фиксированными эффектами (fixed effect model, FE).
Фиксированный эффект pggls – метода включает, как и алгоритм FGLS, два шага. Первый шаг базируется на «внутригрупповой (within) оценке модели FE, второй – в соответствии FGLS. Если в модели FE отсутствует автокорреляция, результаты FE и обобщенного pggls совпадают.
В программной среде R тест на автокорреляцию возмущений i-го объекта в модели FE выполняется при помощи функции pwartest, реализующей алгоритм теста Вулдриджа. Для тестируемой модели получен протокол [11]:
pwartest(mpd, data=PANEL, index=c("P"))
Wooldridge’s test for serial correlation in FE panels
data: plm.model
chisq = 41.901, p-value = 9.603e-11,
т.е. нулевая гипотеза об отсутствии автокорреляции отвергается на любом разумном уровне значимости. Принимая во внимание полученный результат, оценим зависимость туристического потока от объема инвестиций в рамках pggls метода:
pggls(mpd,data=PANEL,index=c("P"), model="within", effect="individual").
Результаты оценки параметров приведены в табл. 4 и 5 соответственно.
Таблица 4
Оценка параметра (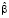 ) влияния в модели FE
) влияния в модели FE
|
|
|
t-статистика |
|
0,1387 |
0,0047 |
29,255 |
R2 = 0,99.
Таблица 5
Оценки параметров местоположения (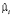 ) в модели FE
) в модели FE
|
Номер области i |
|
|
t |
Номер области i |
|
|
t |
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
1 |
171,616 |
44,512 |
3,8555 |
10 |
2194,622 |
45,985 |
47,7246 |
|
2 |
125,275 |
44,512 |
2,8144 |
11 |
97,248 |
44,514 |
2,1847 |
|
3 |
425,623 |
44,513 |
9,5617 |
12 |
218,468 |
44,512 |
4,9081 |
|
4 |
298,041 |
44,512 |
6,6957 |
13 |
185,395 |
44,512 |
4,1650 |
|
5 |
194,096 |
44,512 |
4,3605 |
14 |
109,132 |
44,512 |
2,4517 |
|
6 |
300,651 |
44,543 |
6,7497 |
15 |
329,538 |
44,521 |
7,4019 |
|
7 |
184,892 |
44,512 |
4,1538 |
16 |
216,638 |
44,512 |
4,8669 |
|
8 |
136,177 |
44,512 |
3,0593 |
17 |
365,423 |
44,575 |
8,1979 |
|
9 |
134,289 |
44,513 |
3,0169 |
18 |
3346,039 |
53,173 |
62,9278 |
Оценки параметров, полученные в рамках модели c фиксированными эффектами при помощи функции plm и при помощи функции pggls, различаются незначительно, но точность и значимость оценок, полученных в рамках метода pggls, выше.
Построенные модели прогнозирования объема туристического потока, в рамках моделей систем внешне не связанных уравнений и моделей для панельных данных, учитывающих неоднородность областей Центрального федерального округа Российской Федерации, будут полезными для разработки маркетинговой стратегии.