Есть множество задач, ответом к которым являются только целые числа. Их называют задачами в целых числах. К ним относятся: уравнения в целых числах (диофантовы уравнения); классические задачи в целых числах (задача о взвешивании, задача о разбиении числа, задача о размене, задача о четырех квадратах), текстовые сюжетные задачи, в которых неизвестные есть целые числа и др. [1–6].
Среди указанных типов задач особую значимость имеют задачи об уравнениях, решаемых в целых числах. Это один из наиболее интересных разделов теории чисел [7–9].
Решение уравнений в целых числах до конца изучено только для уравнений с двумя неизвестными, но это проблематично для уравнений выше второй степени с двумя или более неизвестными.
В данной статье мы рассмотрим решение текстовых сюжетных задач, в которых неизвестные должны выражаться только в целых числах. Причем их однозначное решение возможно лишь при условии существенного использования этого обстоятельства.
Перейдем к решению текстовых задач, в которых требуется сделать выбор, основанный на отборе соответствующих целых чисел.
Задача 1. В группе учится меньше 50 студентов. За индивидуальную работу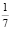 
часть студентов получила оценку «5», 
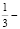«4», а половина студентов получила оценку «3». Остальные работы были оценены оценкой «2», Сколько было студентов, индивидуальные работы которых были оценены неудовлетворительной оценкой?
Решение
Число студентов всегда выражается целым числом. Значит, нам надо найти такое натуральное число меньшее 50 и одновременно делящееся на 7, 3, 2. Единственно возможным таким числом будет число 42.
Решение можно оформить так: пусть x – число студентов. Тогда по условию задачи имеем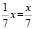 
– студентов получили оценку «5»; 
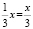– студентов получили оценку «4»; 
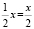– студентов получили оценку «3». Так как x должен одновременно делиться на 7, 3, 2, то таким числом, меньшим 50, будет число 42.
Решение этой задачи можно оформить и так:
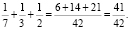
Числитель дроби – число 41 показывает, какое количество студентов получили оценки «5», «4», «3», а знаменатель – число 42 показывает общее количество студентов. И отсюда можно заключить, что оценку «2» получил 1 студент.
Ответ: 6 студентов получили оценку «5»; 14 студентов получили оценку «4»; 21 студент получил оценку «3»; 1 студент получил оценку «2».
Задача 2. Опрос учеников одной из школ выяснил, что 68 % учащихся знают год рождения М.Ю. Лермонтова,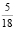 
учащихся умеют доказывать теорему Пифагора, 
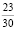учащихся любят ходить в кино и 512 учащихся читали сказку А.С. Пушкина «Руслан и Людмила».
Найдите наименьшее возможное число учащихся в этой школе.
Решение
Пусть х – число учащихся в школе, тогда имеем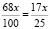 
, 
, 
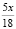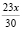. Так как x – это число учащихся, то это число должно выражаться натуральным числом. Из того, что 17 нацело не делится на 25, 5 нацело не делится на 18, 23 нацело не делится на 30, следует, что на эти числа нацело должен делиться x.
Так как 25 = 52, 18 = 2•32, 30 = 2·3·5. Значит, x должен делиться на 2•32•52 = 450.
Но так как по условию задачи x ≥ 512, то наименьшее возможное число учащихся в этой школе равно 900.
Решение этой задачи может быть построено и таким образом, как это описано в решении первой задачи.
Ответ: 900 учащихся.
Задача 3. Три друга купили 13 пирожков, причем Алексей купил в два раза меньше Ивана, а Володя – больше Алексея, но меньше Ивана. Сколько пирожков купил каждый из них?
Решение
Пусть Алексей купил х пирожков, а Володя – у. Тогда Иван купил 2х пирожков. Получаем смешанную систему, составленную из уравнения и неравенства:
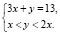
Так как х < у < 2х, то, прибавляя ко всем частям этого неравенства по 3х, будем иметь
4х < у + 3х < 5х, 4х < 13 < 5х.
Отсюда следует, что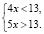 
Решая эту систему неравенств, получаем
.
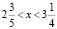Тогда х = 3, 2х = 6. Найдем у:
3х + у = 13, 9 + у = 13, у = 4.
Проверим еще, выполняется ли неравенство х < у < 2х: 3 < 4 < 6. Следовательно, неравенство выполняется.
Ответ: Алексей – 3 пирожка, Володя – 4 пирожка, Иван – 6 пирожков.
Задача 4. Два акционерных общества направили грузовые самосвалы для перевозки сельскохозяйственной продукции общим числом менее 18. Число самосвалов, отправленных вторым акционерным обществом, меньше удвоенного числа самосвалов, отправленных первым акционерным обществом. Если бы первое акционерное общество отправило на 4 самосвала больше числа самосвалов, отправленного вторым акционерным обществом, то все равно это число было бы меньше числа самосвалов, отправленных вторым акционерным обществом. Сколько самосвалов отправило каждое акционерное общество?
Решение
Пусть х и у – число самосвалов, отправленных соответственно первым и вторым акционерными обществами. Получаем систему неравенств:
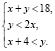
Так как х + 4 < у, у < 2х, то
х + 4 < 2х, х > 4.
Так как х + 4 < у, у < 18 – х (из первого неравенства системы), то
х + 4 < 18 – х, 2х < 14, х < 7.
Тогда 4 < х < 7. Следовательно, х = 5 или х = 6. Рассмотрим оба случая.
1. Пусть х = 5. Система неравенств принимает такой вид:
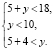
Отсюда 9 < у < 10, а это невозможно.
2. Пусть х = 6. Получаем
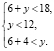
Тогда 10 < у < 12. Следовательно, у = 11.
Ответ: 6 самосвалов и 11 самосвалов.
Задача 5. Имеются ящики двух видов: по 130 кг и 160 кг. Сколько было ящиков первого и сколько второго вида, если груз, помещенный в них, весит 3 тонны? Укажите все решения.
Решение
Обозначим количество ящиков первого вида через х, второго – через у. Получаем уравнение 130х + 160у = 3000, 13х + 16у = 300.
Попробуем воспользоваться делимостью на 13. Для этого 16у представим в виде 13у + 3у, а 300 разделим на 13 с остатком:
13х + 13у + 3у = 13•23 + 1, 3у – 1 = = 13•23 – 13х – 13у.
Так как правая часть последнего уравнения делится на 13, то на это же число должна делиться и его левая часть. Чтобы найти значения у, при которых разность 3у – 1 делится на 13, применим метод перебора. При этом проще не придавать неизвестной у последовательные значения 1, 2, 3 и т.д., а приравнивать 3у – 1 к числам, делящимся на 13: 13, 26, 39, 52, 65 и т.д., выясняя каждый раз, является ли корень соответствующего уравнения целым или дробным. Целые корни получаются в следующих случаях:
3у – 1 = 26, у = 9; 3у – 1 = 65, у = 22
и др. Но уже значение у = 22 слишком велико, так как в этом случае
16у = 16•22 = 352 > 300.
При значении у = 9 из уравнения можно найти х:
13х + 16•9 = 300, 13х = 156, х = 12.
Ответ: 12 ящиков по 130 кг и 9 ящиков по 160 кг.
Задача 6. В классе провели контрольную работу по математике. Средняя оценка мальчиков – 3,8; девочек – 3,5; класса –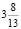 
. Сколько человек писало контрольную работу, если их больше 20 и меньше 30.
Решение
Пусть в классе х мальчиков и у девочек, тогда, согласно условию задачи, имеем
,
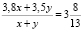или
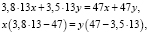
откуда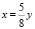 
.
Количество детей, писавших контрольную работу, равно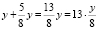 
, где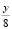 
– целое число (произведение двух чисел, одно из которых простое, будет целым, если и второе число целое).
Заметим, что существует единственное целое k = 2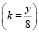 
, такое, что 20 < k < 30. Значит, контрольную работу писали 26 учеников.
Ответ: 26 учеников.
Задача 7. Купили по одной цене несколько карандашей и по одной и той же цене несколько ручек. За карандаши заплатили 10 р. 56 к. Известно, что карандашей купили на шесть больше, чем ручек, а цена карандаша более чем на 1 рубль превосходит цену ручки. Сколько купили карандашей?
Решение
Из условия видно, что карандашей купили не менее семи и цена карандаша больше одного рубля. Отсюда следует, что карандашей не более десяти (иначе за них заплатили бы больше 11 руб.). Таким образом, количество купленных карандашей – одно из чисел 7, 8, 9, 10. Кроме того, цена одного карандаша в копейках – натуральное число, следовательно, 1056 делится нацело на одно из чисел 7, 8, 9, 10. Из них только число 8 является делителем числа 1056, значит, купили 8 карандашей.
Ответ: 8 карандашей.
Задача 8. В сарае имеются гуси и кролики. Всего у этих гусей и кроликов 50 голов и 140 ног. Сколько гусей и сколько кроликов имеется в сарае?
Решение
Пусть в сарае х гусей и у – кроликов. Тогда имеем систему двух уравнений с двумя неизвестными:
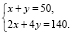
Сократив обе части второго уравнения на 2, будем иметь
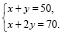
Вычитая из второго уравнения системы первое, получим у = 20; тогда х = 30.
Ответ: 20 кроликов, 30 гусей.
Задача 9. В аудитории присутствуют преподаватель и несколько обучающихся. Найти число обучающихся, если известно, что возраст преподавателя на 24 года больше среднего возраста обучающихся и на 20 лет больше среднего возраста всех присутствующих в аудитории.
Решение
Пусть х – средний возраст обучающегося, у – количество обучающихся.
Запишем уравнение, которое мы составим по условию задачи (читателю следует объяснить, как оно составлено).
.
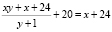Так как у + 1 ≠ 0, то мы можем обе части уравнения умножить на это выражение. Будем иметь
ху + х + 24 + 20у + 20 = ху + 24у + х + 24,
4у = 20.
у = 5.
Ответ: 5 обучающихся.
Задача 10. Встретились два математика: Петров и Сидоров. Сидоров сказал: «Мы с тобой давно не встречались, а потому я не знаю, как у тебя сложилась семейная жизнь». Петров ответил: «У меня три сына, и, зная, что ты тоже математик, их возраст узнай сам. Даю условие: произведение их возрастов равно 36». Сидоров, подумав, ответил: «Мне не хватает данных». Петров добавляет: «Сумма их возрастов равна номеру уходящего трамвая». Сидоров, взглянув на трамвай, ответил: «Мне хватает данных». Петров сказал: «Забыл тебе сказать, что у старшего сына волосы рыжие». Сидоров ответил: «Теперь я все понял!» и назвал возраст сыновей. Какого возраста сыновья Петрова?
Решение
Перебрав все возможные произведения трех натуральных чисел (делители числа 36) Сидоров получил:
1•1•36 = 36; 2•3•6 = 36; 2•2•9 = 36;
3•12•1 = 36; 3•3•4 = 36; 6•6•1 = 36;
2•18•1 = 36; 4•1•9 = 36.
Конечно, получив восемь различных вариантов, Сидоров указал на недостаточность информации.
Сообщение о сумме возрастов сыновей, которая равна номеру трамвая, заставило Сидоров просуммировать полученные варианты чисел:
1 + 1 + 36 = 38; 2 + 3 + 6 = 11;
2 + 2 + 9 = 13; 3 + 12 + 1 = 16; 3 + 3 + 4 = 10;
6 + 6 + 1 = 13; 2 + 18 + 1 = 21; 4 + 1 + 9 = 36.
Сидоров сообщает о недостаточности данных, так как трамвай был номером 13 (число 13 дают два различных набора чисел: 2, 2, 9 и 6, 6, 1 и, какой из них взять, неизвестно – под первые два условия походят оба).
Сообщение о старшем сыне (ключевое слово «старший», а не слово, сообщающее о цвете волос), позволяет Сидорову ответить на заданный вопрос: двум сыновьям по 2 года, а одному 9 лет.
В наших работах [2, 10, 11] и в работах [12, 13] читатель найдет много других интересных задач, решаемых в целых числах.