Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Одним из путей повышения качества молочной продукции является создание инновационных методов контроля и управления, т.е. создание автоматизированных систем управления технологическими процессами производства молока.

Для достижения этой цели в работе [1] предложена трехуровневая система, состоящая из системы омагничивания молока; системы контроля качества молока с датчиком, использующим метод ядерного магнитного резонанса (ЯМР); частотно-импульсной системы стабилизации (ЧИСС) напряженности магнитного поля.

Система омагничивания молока обеспечивает улучшение качественных характеристик молока за счет применения метода ядерного магнитного резонанса ЯМР. Аппарат электромагнитной обработки молока, принцип его работы и блок-схема системы представлены в работе [1].

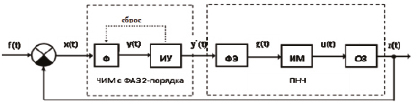
Рис. 1. Структурная схема ЧИСС напряженности магнитного поля

Система контроля качества молока основана на использовании датчиков ЯМР, которая позволяет с высокой степенью точности контролировать качество выпускаемой продукции и обнаружить любую химическую подделку.

В настоящей работе рассматривается частотно-импульсная система стабилизации (ЧИСС) напряженности магнитного поля, функционирующей аналогично системе, приведенной в [2].

ЧИСС индукции (напряженности) магнитного поля – замкнутая система, состоящая из Σ-частотно-импульсного модулятора с фильтром в виде апериодического звена (ФАЗ) 2 го порядка и приведенной непрерывной части (ПНЧ), структурная схема системы приведена на рис. 1.

На входе системы действует стационарный нормальный случайный процесс f(t) с корреляционной функцией с известной корреляционной функцией .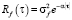

Приведенная непрерывная часть ПНЧ состоит из последовательного соединения управляемого объекта с запаздыванием, исполнительного механизма (ИМ) и формирующего элемента (ФЭ), задающего требуемую форму управляющих импульсов.

В общем случае ПНЧ характеризуется как нелинейная динамическая система со случайными параметрами и представима некоторым функциональным уравнением следующего вида [3, 4]:

z(t) = H[λ, τ₀, z(τ), g(τ)/t0 ≤ τ ≤ t], (1)

где H – непрерывный нелинейный функционал; параметр λ характеризует случайность параметров функционала H; g(t) – последовательность управляющих случайных импульсов заданной формы; τ₀ – время запаздывания управляемого объекта с запаздыванием (ОЗ) [5].

Σ – частотно-импульсный модулятор (Σ-ЧИМ) второго порядка представляет собой последовательное соединение фильтра (Ф), реализованного в виде апериодического звена 2 порядка и импульсного устройства ИУ (рис. 1).

В фильтре осуществляется некоторое динамическое преобразование непрерывного процесса x(t) в сигнал y(t). Импульсное устройство ИУ генерирует единичный δ-импульс в тот момент времени, когда выходной сигнал фильтра Ф достигает порогового значения Δ и осуществляет обнуление всех накопителей энергии, которые входят в состав фильтра (осуществляется операция сброса). Уравнение движения Σ-частотно-импульсного модулятора второго порядка состоит из уравнения движения фильтра Ф и уравнений, определяющих моменты появления и знак импульсов, и операции сброса.

Фильтр Σ-ЧИМ второго порядка, описывается в виде апериодического звена 2 порядка передаточной функцией

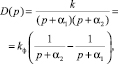(2)

где 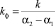– коэффициент усиления апериодического звена 2 порядка, а α1, α2 – время инерционности.

Содержательное описание и математическая формулировка задачи параметрического синтеза ЧИСС индукции (напряженности) магнитного поля даны соответственно в [1] и [2].

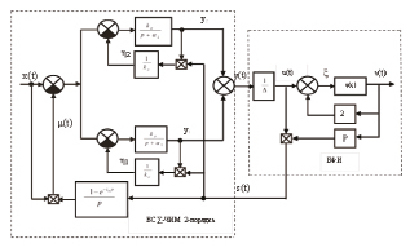
Рис. 2. Структурная схема модели Σ-ЧИМ 2 порядка

Процедура параметрического синтеза ЧИСС индукции (напряженности) магнитного поля состоит из трех этапов:

1. Структурное преобразование Σ-ЧИМ 2-го порядка, т.е. построение структурной модели, нелинейной эквивалентной исходному модулятору системы;

2. На основе структурной модели разработка нелинейных моделей в классе рядов Вольтерра и статистически линеаризованных моделей.

3. Оценка настроечных параметров (параметрический синтез) ЧИСС напряженности магнитного поля.

Структурное преобразование Σ-ЧИМ второго порядка. Процедура построения нелинейной системы, эквивалентной Σ-ЧИМ второго порядка, не содержащей параметрических обратных связей, приведена в работе [1] (рис. 2).

Она состоит из блока сброса (БС) и блока формирования импульса (БФИ). Блок БС осуществляет функции фильтра (Ф) модулятора со сбросом, а блок БФИ формирует управляющие импульсы в виде δ-импульсов.

1. Математические модели частотно-импульсной системы стабилизации напряженности магнитного поля. Формирование математической модели ЧИСС напряженности магнитного поля в классе функциональных рядов Вольтерра распадается на три этапа: на первом этапе строится вольтерровская модель Σ-ЧИМ второго порядка; на втором этапе – вольтерровская модель разомкнутой системы ЧИСС и на третьем этапе – вольтерровская модель замкнутой системы ЧИСС [2].

Вольтерровская модель Σ-ЧИМ второго порядка описывается в виде

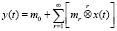, (3)

где символом 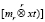обозначена r-мерная свертка импульсных характеристик объекта с запаздыванием 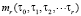и функции 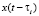, , 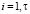т.е.

.

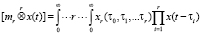Изображения ядер ряда (3) получены в [2] в следующем виде

, ,

,

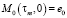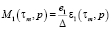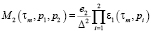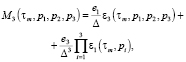(4)

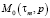где и 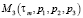– соответственно изображения ядер фильтра Ф со сбросом динамического частотно-импульсного модулятора системы, e0, e1, e2, e3 – постоянные параметры, характеризующие поведение блока формирования импульсов БФИ модулятора [2], τ_m – параметр модификации, Δ – порог импульсного устройства ИУ.

Изображения ядер фильтра Ф со сбросом Σ-ЧИМ второго порядка в [2] получены в виде

,

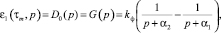
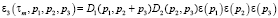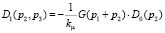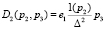, . (5)

Вольтерровская модель разомкнутой системы (последовательное соединение модулятора и ПНЧ) имеет следующий вид

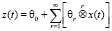. (6)

где 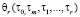– импульсные характеристики модели (6).

Изображения для первых трех ядер в терминах многомерного преобразования Лапласа [3] определяются из выражений

; ;

;

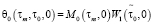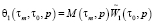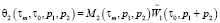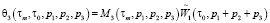. (7)

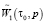– передаточная функция ПНЧ [2].

Вольтеровская модель замкнутой системы в виде

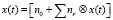, (8)

где 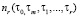– импульсные характеристики модели (8).

Изображения первых трех ядер ряда (8) получены в виде

;

;

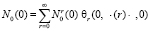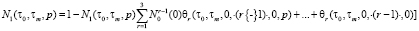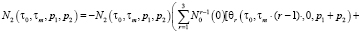
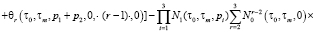
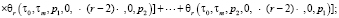
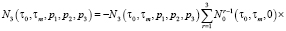
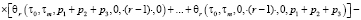
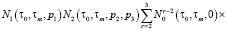
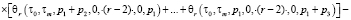
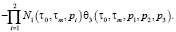
Полученные вольтерровские модели (3), (6), (8) можно непосредственно использовать для статистического анализа и синтеза ЧИСС напряженности магнитного поля. В некоторых практических случаях можно поступиться точностью вычислений ради получения приемлемых результатов.

С этой целью формируются статистически линеаризованные модели ЧИСС напряженности магнитного поля в виде

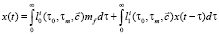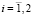, . (9)

Статистическая линеаризация ЧИСС напряженности магнитного поля может быть проведена двумя способами: раздельная и оптимальная линеаризация. В данной работе для оценки настроечных параметров управляющего устройства использована полученная оптимальной линеаризацией статистически линеаризованная модель (9), изображения ядер которой имеют следующий вид:

,

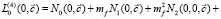
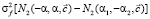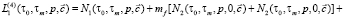
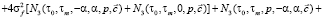
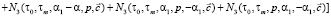, (10)

где 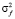, α – дисперсия и коэффициент спада корреляционной функции случайного процесса f(t).

Оценка настроечных параметров ЧИСС напряженности магнитного поля. Использование при синтезе ЧИСС напряженности магнитного поля ее вольтерровской модели позволяет получить асимптотически точный результат. Оценка настроечных параметров ЧИСС напряженности магнитного поля на базе статистических линеаризованных моделей сводится к задаче оптимизации вида [6, 7]

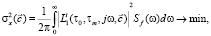(11)

где 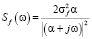– спектральная плотность входного процесса, 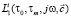определяется из (10), 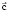– вектор оптимизируемых параметров.

Оптимизируемыми параметрами ЧИСС напряженности магнитного поля являются:

коэффициент усиления фильтра – kф; первая постоянная времени фильтра Σ-ЧИМ – 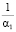; вторая постоянная времени фильтра Σ-ЧИМ – 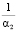; порог срабатывания импульсного устройства – Δ; длительность управляющих импульсов – h_u; амплитуда управляющих импульсов – k_u.

Для ЧИСС напряженности магнитного поля экспериментальным путем получены следующие значения оптимальных настроечных параметров регулятора (таблица), обеспечивающие заданные значения напряженности магнитного поля.

Оптимальные настроечные параметры ЧИСС напряженности магнитного поля

Полученные оптимальные настроечные параметры регулятора позволили обеспечить необходимую точность стабилизации напряженности магнитного поля, что привело к уменьшению расхода молока свертывающего фермента при выработке сыров и к изменению показателя кислотности и вязкости.