Один из блоков системы капиллярного электрофореза (в дальнейшем – прибора) – модуль термостатирования кварцевого капилляра. Термостабилизация осуществляется отведением Джоулева тепла простым и дешёвым способом жидкостного охлаждения [1]. Но практика показывает – данный подход имеет ряд недостатков: непродолжительный срок службы насосов (3–5 лет), протечки в точках стыковки элементов гидравлической магистрали, высокая вероятность загрязнения теплоносителя хлопьевидными осадками гидроксокомплексов металлов при использовании металлических радиаторов и хлорированной воды.
Поэтому возникла техническая задача – замена жидкостной системы термостабилизации кварцевого капилляра прибора [1] на модуль суховоздушного термостатирования с элементом Пельтье (ЭП). Требуемое значение температуры капилляра Tх = 20 °C, допустимый разброс ΔT = ± 0,2 °C. Диапазон температур T1 в лаборатории – 20 … 35 °С. ЭП помещается в кассету прибора, а на его поверхность укладывается и закрепляется трубка капилляра. Однако при разработке системы возникает проблема – в документации на выпускаемые ЭП недостаточно информации о многих их особенностях [2]. Из неё нет возможности извлечь информацию о температурной зависимости DTЭП(UЭП) и угловом коэффициенте d(ΔTЭП)/dUЭП, а также об инерционных и частотных свойствах ЭП. Указанные данные необходимы для разработки электронного регулятора, обеспечивающего устойчивое термостатирование с малой ошибкой. В трудах ведущих специалистов в области термоэлектричества – А.Ф. Иоффе [3], Л.В. Булата [4, 5], Е.К. Иорданошвили [3, 5] и многих других не – приводится информация об инерционных и частотных свойства ЭП, а также о способах их исследования.
Так как процесс установления температуры инерционен – длится несколько минут, проблематично снятие полной частотной характеристики (ЧХ) ЭП обычным мануальным способом, по точкам. Процесс получения ЧХ длителен, в течение его затруднительно поддержать постоянной температуру окружающей среды. Но ЧХ объекта связана с переходной характеристикой (ПХ). Однако из-за той же инерционности ЭП его ПХ невозможно зафиксировать обычным осциллографом. Для этого необходима автоматизированная система для исследования ПХ – из формирователя ступенчатого воздействия и регистратора.
Таким образом, при разработке системы термостатирования потребовалось решить следующие задачи:
1) получить для используемого ЭП зависимости ΔTх(UЭП) и значения d(ΔTЭП)/dUЭП;
2) разработать автоматизированную систему для получения ПХ ЭП, получить её;
3) по данным о ПХ получить частотную характеристику ЭП;
4) для проверки адекватности полученных характеристик ЭП получить математическую модель общей ЧХ варианта разомкнутой системы термостатирования;
5) определить параметры электронного регулятора, обеспечивающие устойчивую работу системы термостатирования с ошибкой регулирования ΔTх ≤ 0,2 °C.
Для ЭП получены экспериментальные зависимости разности температур холодной Tх и горячей Tг плоскостей
ΔTЭП = Tх – Tг ,
от величины приложенного напряжения UЭП (рис. 1, а и б). В ходе эксперимента для отвода теплоты от горячей стороны ЭП использованы радиатор с кулером. Напряжение питания ЭП устанавливалось с помощью источника питания Б5-46 с разрешающей способностью 0,01 В и вольтметра В7-34А с разрешающей способностью до 100 мкВ и погрешностью измерения не более 0,013 %. Термопарами типа K и измерителями 2ТРМ1 фирмы ОВЕН измерялась температура горячей и холодной сторон ЭП с разрешающей способностью 0,01 °C и погрешностью 0,5 %. Зависимости получены при разных значениях напряжения питания кулера Ufan и значениях температуры окружающей среды T1 = {22,1, 23,9, 25,2, 26,6 и 28,3} °C.
Анализ результатов экспериментов (графики рис. 1, а и б) показал – зависимости ΔT(UЭП) практически линейны, а коэффициент d(ΔTЭП)/dUЭП принимает значения в диапазоне от 6,463 до 7,555 °C. Причём не наблюдается какой-либо зависимости коэффициентов от температуры окружающей среды при одном и том же значении Ufan.
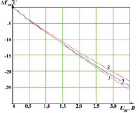
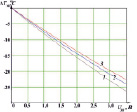
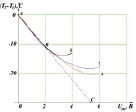
а) T1 = 22,1 °C б) T1 = 28,3 °C в) T1 = 25,5 °C
Рис. 1. Температурные зависимости элемента Пельтье: а) и б) – разности температур холодной и горячей стороны; в) – холодной стороны и окружающей среды; 1 – диаграмма при Ufan = 0 В; 2 – при Ufan = 5 В; 3 – при Ufan = 12 В; Ufan – напряжение кулера
Так же получены зависимости только для холодной стороны – (Tх – T1) от UЭП при тех же потоках и температуре T1 = 25,5 °C (рис. 1, в). Установлено – только при активном охлаждении диапазон температур с линейной зависимостью Tх(UЭП) превышает амплитуду колебаний температуры в лаборатории – 15 °С. Поэтому решено остановиться на таком виде отвода тепла с питанием кулера Ufan = 12 В, а за коэффициент d(DTЭП)/dUЭП принято его среднее арифметическое экспериментальное значение при Ufan = 12 В
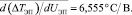(1)
Разработана автоматизированная система исследования переходной характеристики ЭП (рис. 2), которая реализована на той же плате разработанного макета системы термостатирования, В системе генератор импульсов по программе микроконтроллера (МК) формирует ШИМ-сигнал с фиксированным коэффициентом заполнения DDcool, а данные о разности температур ЭП фиксируются в EEPROM МК. DDcool подобран экспериментально так, чтобы за время переходного процесса разность показаний АЦП1 и АЦП2 (рис. 2) изменялись не менее, чем на 20 квантов (один квант – не более 5 % от изменения значений ПХ). Данные фиксируются с момента «пуска» генератора до установления ПХ с погрешностью до одного кванта, что в итоге соответствует 3,7 %. Содержимое EEPROM считывается программатором в ПЭВМ и обрабатывается исследователем.
Получены экспериментальные ПХ при температурах окружающей среды T1 = {22,1, 25,2 и 28,3} °C. Установлено – в ходе измерения одной ПХ температура T1 не изменялась в пределах одного знака после запятой и при разных T1 ПХ не отличались (диаграмма 1 рис. 3). Также результаты эксперимента показывают – функция ПХ близка к экспоненциальной (диаграмма 2 рис. 3) и описываемой выражением
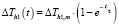. (2)
Постоянная τ переходного процесса определена по критерию «3·τ»
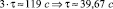. (3)
Функция ПХ (2) соответствует апериодическому звену, поэтому ЧХ ЭП имеет вид
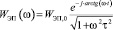, (4)
где
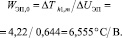(5)
Применение полученных результатов рассмотрим на примере системы термостатирования (схема рис. 4) с электронным ПИ-регулятором. ПИ-регулирование выбрано ввиду бесконечно малой теоретической ошибки регулирования и нетребовательности к высокому быстродействию системы – нет необходимости усложнять регулятор до ПИД.
Итак, выведем функции ЧХ разомкнутой системы.
Напряжение UЭП управляется с сигналом, формируемым ШИМ-компаратором МК Atmega 8 [6, с. 181] (рис. 4). Коэффициент заполнения ШИМ-сигнала Dcool зависит от разницы между температурами заданной T0 = 20 °C и окружающей среды T1, а также между заданной T0 и текущей температурой Tх элемента Пельтье, и определяется суммой
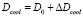. (6)
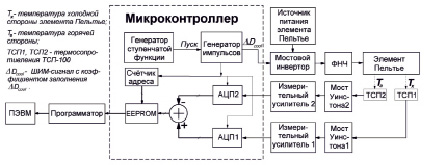
Рис. 2. Система для исследования переходной характеристики
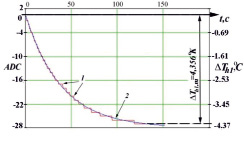
Рис. 3. Переходные характеристики (ПХ) элемента Пельтье: ADC – значения разности АЦП1 и АЦП2; 1 – экспериментальная ПХ; 2 – аппроксимирующая функция ПХ
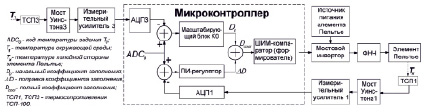
Рис. 4. Структурная схема системы термостатирования
В выражении (6) D0 – начальное значение коэффициента заполнения
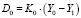, (7)
где K0 – коэффициент «Масштабирующего блока K0», зависит от характеристик ЭП;
Y0 – двоичный код заданной температуры T0;
Y1 – код заданной температуры окружающей среды T1
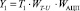, (8)
WАЦП = Ymax/Uref – коэффициент передачи 8-битного АЦП;
Ymax – полная шкала АЦП;
Uref – опорное напряжение АЦП;
WT-U – общая функция передачи измерительного канала «ТСП3» – «Моста Уинстона 3» – «Измерительного усилителя 3».
Схемы, параметры элементов и определяющие характеристики обоих измерительных каналов практически одинаковы. Переходные процессы в ЭП длятся сотни секунд – на порядки дольше, чем в перечисленных узлах, поэтому передаточную характеристику WT-U(w) можем считать постоянной. Её значение
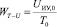, (9)
где UИУ,0 – выходное напряжение измерительного усилителя при температуре T = T0.
Коэффициент D0 «вычисляется» подпрограммой «Блока K0» считыванием заранее посчитанных формулой (7) значений из таблицы Flash-памяти МК. Адрес в таблице линейно зависит от значения, эквивалентного T1 и полученного через «АЦП3». Элементы таблицы D0 соответствуют значениям температуры в диапазоне от 0 до 39,06 °С с шагом 0,151 °С.
Поправка DDcool – результат функционирования подпрограммы «ПИ-регулятора» (рис. 4), и определяется выражением
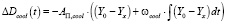, (10)
где AП,cool – коэффициент пропорционального закона;
wcool, с-1 – частота перегиба ЛАЧХ ПИ-регулятора;
Yх – код температуры Tх холодной стороны ЭП.
Параметры и характеристики каналов измерения Tх и T1 одинаковы, поэтому
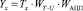. (11)
Функция передачи ПИ-регулятора имеет вид [7, с. 180]
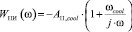. (12)
ФНЧ – LC-фильтр низших частот второго порядка. Его частота среза wc подобрана так, что гармоники переменной составляющей ШИМ-сигнала давятся более чем в 100 раз. Выражение для его ЧХ имеет вид [8, с. 141]
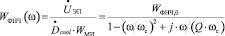, (13)
где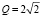 
, WМИ = 1 – коэффициент передачи мостового инвертора, WФНЧ,0 = 12 В – отношение разниц напряжений ЭП и коэффициентов заполнения в двух устойчивых состояниях.
Для получения общей ЧХ разомкнутой системы проанализируем связи между переменными системы рис. 4. Частотные зависимости для переменных ΔDcool и D0
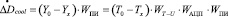, (14)
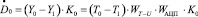. (15)
На основании схемы (рис. 4), а также выражений (14) и (15)
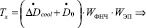
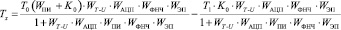. (16)
Устойчивость системы определяют свойства передаточной функции разомкнутой цепочки WT-U – WАЦП – WПИ – WМИ – WФНЧ – WЭП – произведение в знаменателях выражения (16)
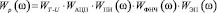. (17)
Для определения параметров ПИ-регулятора исследованы свойства нормированных ЧХ (диаграммы 2 и 3 рис. 5) прямого звена – той же цепочки без ПИ-регулятора:
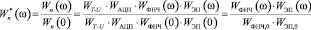. (18)
Параметры ПИ-регулятора определены в поиске компромисса между устойчивостью и скоростью переходных процессов. Для нормированных ЧХ ПИ-регулятора (диаграммы 1 и 4 рис. 5) принято – ωcool = 1/τ = 2·π·fЭП. Анализ ЧХ полной разомкнутой системы показал – выбор даёт запас устойчивости 90 ° (диаграммы 2 и 3 рис. 5). Смещение wcool вправо уменьшит запас устойчивости (диаграммы 1 и 4 рис. 5), влево – увеличит время установления температуры. Из условия Wр(0) = 1 и на основании (12) определяется Ap,cool
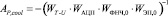. (19)
Изготовленный электронный макет схемы рис. 4 прошёл испытания в статическом режиме при почти неизменных значениях температуры T1 – 22, 24 и 28 °С. Для контроля температуры ЭП использовался дополнительный датчик ТСП-100 и 6,5-разрядный мультиметр В7-34А в режиме омметра на пределе 0,1 кОм (от 1 мОм до 120,000 Ом). После установления температуры ЭП показания мультиметра колебались от 107,64 до 107,70 Ом, что соответствует диапазону температур от 19,85 до 20,01 °C.
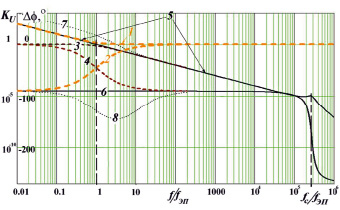
Рис. 5. Частотные характеристики: 1, 2 – АЧХ и ФЧХ ПИ-регулятора; 3, 4 – АЧХ и ФЧХ разомкнутой системы без ПИ-регулятора; 5, 6 – АЧХ и ФЧХ разомкнутой системы при ωcool = 2·π·fЭП; 2, 3 – АЧХ и ФЧХ разомкнутой системы при ωcool = 2·π·fЭП; fЭП = 1/(2πω) – частота среза элемента Пельтье; fc – частота среза ФНЧ
Таким образом, для элемента Пельтье разработан способ получения зависимости разности температур ΔTх от напряжения UЭП, а также его ЧХ с помощью разработанной системы исследования ПХ. Указанные характеристики необходимы для разработки систем термостатирования на основе элементов Пельтье и электронных регуляторов (П, ПИ и ПИД).