Тросовые манипуляторы параллельной структуры обладают множеством потенциальных преимуществ перед классическими (последовательными) манипуляторами, в том числе большей рабочей областью, точностью, а главное, более высокими коэффициентами полезной нагрузки. По сравнению с традиционными параллельными манипуляторами с жесткой связью, тросовые конструкции способны обеспечить работу на значительно большем пространстве. Кроме того, их относительно низкие массовые и инерционные показатели облегчают работу на более высоких скоростях. Однако есть отличительная черта подобных конструкций, кабели могут тянуться, но не толкать, это приводит к односторонним ограничениям, которые усложняют моделирование и анализ манипуляторов с гибкими связями. Полный контроль всех степеней свободы тросовым манипулятором может быть обеспечен если тросы будут всегда оставаться напряженными, и обычно требуется минимум одной степени избыточности приведения в действие. Тросовые роботы также страдают от ограниченного момента сопротивления (воздействия). Для борьбы с этими ограничениями в литературе были предложены различные методы, каждый из которых имеет свои преимущества и недостатки [1].
Целью данной работы является исследование системы планирования траектории манипулятора параллельной структуры, определение программных методов, позволяющих нивелировать ограничение момента сопротивления тросового манипулятора.
Общий вид манипулятора с гибкими звеньями представлен на рис. 1.
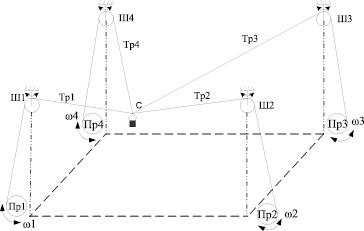
Рис. 1. Общий вид манипулятора с гибкими звеньями
На рис. 1 приняты следующие обозначения:
Пр1–Пр4 – электрический привод звеньев 1–4 манипулятора соответственно; Ш1–Ш4 – шкивы звеньев 1–4 соответственно; Тр1–Тр4 – звенья (тросы) 1–4 соответственно; С – схват; ω1–ω4 – угловые скорости электроприводов звеньев 1–4 соответственно; ω1–ω4 – углы поворота шкивов звеньев 1–4 соответственно.
В работах [1, 2] приведены решения прямой и обратной задач кинематики по положению и скорости для структуры, представленной на рис. 1, на основании которых предложены два метода планирования траектории перемещения, один из которых обладает существенной методической погрешностью по точности, второй предъявляет высокие требования к быстродействию программно-аппаратного комплекса, реализующего систему управления манипулятором.
Задачу формирования управляющих воздействий на электроприводы звеньев можно сформулировать следующим образом:
– участок траектории задан как отрезок прямой (рис. 2);
– известны абсолютные координаты положения схвата и обобщённые координаты всех звеньев в начале и конце отрезка;
– текущие значения обобщённых координат доступны для измерения в любой точке траектории перемещения;
– скорость перемещения по траектории и частота дискретизации формирования управляющих воздействий по скорости на привода звеньев заданы.
В основу метода планирования траектории положен расчёт задания мгновенного значения скорости по направлению каждой из обобщенных координат в зависимости от вектора скорости, направленного по траектории перемещения в абсолютных координатах через равные промежутки времени. На рис. 2 показан пример взаимного положения векторов заданной скорости перемещения по траектории и вектора скорости одной из обобщённых координат.
На рис. 2 приняты следующие обозначения: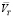 
– вектор скорости перемещения схвата по траектории; 
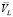– вектор скорости перемещения звена манипулятора; φi – угол между векторами 
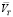и 
.
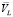Модуль мгновенной скорости перемещения любого из звеньев манипулятора определяется исходя из соотношения:
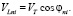(1)
Здесь индекс n соответствует номеру звена, индекс i – номеру текущей итерации.
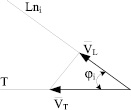
Рис. 2. Векторная диаграмма скоростей перемещения схвата по заданной траектории
Угол φi может быть определён исходя из треугольника ΔONiM (рис. 3), который образован отрезком траектории NiM, начальным (отрезок ONi) и конечным (OM) положением для звена n манипулятора (рис. 1) по теореме косинусов.
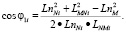(2)
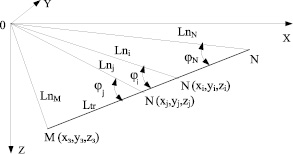
Рис. 3. Пример положения траектории перемещения схвата в абсолютных координатах x, y, z
Конечные значения обобщённой (точка М отрезка траектории) и декартовых координат известны по условию задачи. Текущее значение обобщённой координаты (отрезок ОN треугольника) известно по данным датчика положения системы управления. Текущее значение декартовых координат точки Ni может быть определено путём решения прямой задачи кинематики манипулятора при условии, что значения остальных обобщённых известны исходя из условия задачи. Текущая длина отрезка NMi, общего для всех звеньев, определяется по декартовым координатам текущей и конечной точек траектории в пространстве зоны обслуживания манипулятора.
Перемещение по траектории осуществляется от одной опорной точки к другой с фиксированной обобщённой скоростью по каждой из координат. Расчётное количество элементарных отрезков, на которые разбит отрезок траектории, можно определить из соотношения 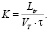[3]
(3)
Здесь Ltr – исходная длина отрезка траектории; τ – время одной итерации.
Знаменатель уравнения (3) соответствует элементарному перемещению Δl за время одной итерации τ. Шаг за одну итерацию по каждой из декартовых координат определяется из соотношений
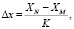
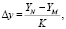
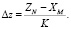(4)
В уравнениях (4) индекс N соответствует координатам начала отрезка траектории, индекс М – координатам конца.
Ошибка предложенного метода планирования может быть представлена двумя составляющими: ошибкой по отклонению по заданной траектории и абсолютной ошибкой, обусловленной разностью векторов мгновенных скоростей по траектории и обобщенной координате, как показано на рис. 4.
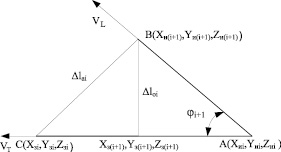
Рис. 4. Методические ошибки метода планирования
Расчёт абсолютной ошибки для оценки точности перемещения по заданной траектории существенного значения не имеет, так как корректируется на каждом шаге за счёт того, что в расчётах используется истинное значение координат начальной точки очередной итерации – Xи(i+1),Yи(i+1),Zи(i+1) . Величина этой ошибки определяется рассогласованием истинного и заданного значений скоростей перемещения по траектории, что является свойством предлагаемого метода [4]. Рассмотрение этого вопроса выходит за рамки данной работы.
Величина относительной ошибки Δloi при известных координатах вершин ΔАВС (рис. 4) достаточно просто может быть определена методами аналитической геометрии [5]. Здесь необходимо отметить, что абсолютные координаты Xи(i+1),Yи(i+1),Zи(i+1) определены исходя из трёх обобщённых координат и текущие координаты начала отрезка корректируются по сравнению с идеализированным, представленным на рис. 2 на каждом шаге отработки траектории перемещения. Из выражения 3 очевидно, что величина относительной ошибки зависит от соотношения скорости перемещения по траектории VT и частоты дискретизации 1/τ формирования управляющих воздействий на электроприводы звеньев манипулятора.
Представленный метод планирования опробован на натурном макете манипулятора, выполненного в соответствии с кинематической схемой, приведенной на рис. 1. Зона обслуживания макета манипулятора представлена параллелепипедом 2100х1600х2500 мм. Система управления иерархическая двухуровневая.
На рис. 5 приняты следующие обозначения: ПК – персональный компьютер; Зв1–Зв4 – информационно-управляющие системы звеньев 1–4 манипулятора соответственно; ОП – объект перемещения; РПУ – ручной пульт управления.
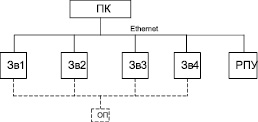
Рис. 5. Общая функциональная схема управления манипулятором
Как следует из рис. 5, система управления иерархическая двухуровневая. Первый уровень реализован на персональном компьютере программным способом и решает следующий круг задач управления:
– начальную инициализацию системы управления;
– сбор и анализ параметров состояния систем управления Зв1–Зв4;
– формирование управляющих воздействий на САУ электроприводов звеньев манипулятора;
– отображение состояния параметров САУ в процессе перемещения.
Второй уровень включает в себя САУ каждого из звеньев и информационного обеспечения процесса управления верхнего уровня иерархии. Связь между всеми устройствами осуществляется на основе проводной линии связи в стандарте Ethernet протокол UDP.
Задача верхнего уровня управления решена с помощью программной информационно-управляющей оболочки, реализованной на языке С++ под управлением операционной системы Windows 7.
На рис. 6 представлена экранная копия интерфейса пользователя программы управления манипулятором в режиме перемещения по заданной траектории. Текущее положение схвата во фронтальной и горизонтальной проекциях зоны обслуживания непрерывно выводится в соответствующие графические окна экранного интерфейса. Численные значения параметров, упомянутые выше, выводятся в соответствующие окна таблиц экранного интерфейса. Заданное положение схвата определяется положением ползунковых задатчиков. Заданная траектория перемещения также отображается в графических окнах соответствующих фронтальной и горизонтальной проекций зоны обслуживания. В режиме перемещения в графических окнах истинная траектория накладывается на заданную, а текущие значения декартовых и обобщённых координат и относительной ошибки выводятся в соответствующие ячейки таблиц.
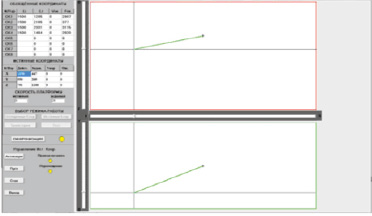
Рис. 6. Экранная копия окна интерфейса управления манипулятором
В процессе опытной эксплуатации показана полная работоспособность предложенного метода планирования траектории перемещения схвата манипулятора. Максимальное значение отклонения от заданной траектории при VT = 200 мм/с и τ = 20 мс составило Δlomax = 5 мм. При VT = 50 мм/с и τ= 20 мс значение относительной ошибки колеблется в пределах плюс минус 4 дискрет измерения обобщённых координат (одна дискрета равна 0,154 мм).
Выводы
В работе рассмотрен один из методов планирования траектории перемещения схвата манипулятора, основанный на расчёте значения мгновенной скорости по каждой из обобщённых координат и формирования на основе этих значений управляющих воздействий на САР электроприводов звеньев. Определена величина погрешности метода и факторы на неё влияющие. Представлены результаты натурного моделирования на реальном макете устройства. Показан возможный вариант интерфейса пользователя программы управления манипулятором в режиме перемещения по заданной траектории. Показана общая функциональная схема управления манипулятором.