Общая информация о методе
Метод составного вибратора широко используется для измерения скорости звука, упругих модулей E и G поликристаллов, а также упругих постоянных сij монокристаллов твердых тел [1, 2]. Метод составного вибратора позволяет получить сведения также о неупругих свойствах материала. Данные по неупругим свойствам получаются из измерения декремента затухания в широком диапазоне колебательной деформации, когда в материале образца возникает нелинейное амплитудно-зависимое поглощение. Таким образом, его можно применять для измерения внутреннего трения твердых тел.
При измерении упругих характеристик материалов метод основан на измерении резонансных частот продольных и крутильных колебаний в системе «преобразователь колебаний – образец». Как правило, в качестве активного элемента для возбуждения колебаний [3] используется кварцевый пьезоэлектрический преобразователь (рис. 1), обладающий высокой добротностью и стабильностью параметров в широком ультразвуковом диапазоне частот.
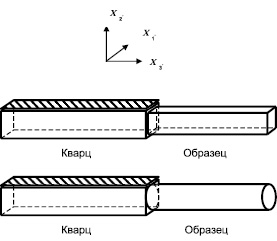
Рис. 1. Двойной составной пьезоэлектрический вибратор с образцами прямоугольного и кругового поперечных сечений в лабораторной системе координат
Измерения частоты механического резонанса пьезокварца и системы пьезокварц – образец позволяют рассчитать собственную частоту образца fs:
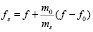, (1)
где f – резонансная частота системы пьезокварц – образец (собственная частота вибратора),
f0 – резонансная частота пьезокварца (преобразователя),
m0 – масса кварца,
ms – масса образца.
Упругие свойства материалов затем рассчитывают из собственных частот соответствующих колебаний образцов.
Такой составной вибратор, состоящий из кварца и образца, называется двойным.
Особенности метода составного вибратора
Несмотря на то, что метод составного вибратора достаточно хорошо разработан, и его кажущуюся простоту, он имеет ряд ограничений и особенностей.
1. Его можно использовать только при температурах до 573 °С, так как при этой температуре происходит полиморфный фазовый переход α-кварца в β-кварц, решетка которого принадлежит гексагональной сингонии, и пьезоэлектрические свойства кварца резко ухудшаются. Для измерений при высоких температурах используют тройной вибратор с буферным стержнем. Детальный анализ работы составного тройного пьезоэлектрического вибратора выполнен в литературе.
2. Формула (1) получена для веществ с малым затуханием путем анализа электрической эквивалентной цепи составного вибратора и тем точнее, чем меньше затухание. При исследовании материалов с большим внутренним трением (Q–1 > 0,1) она не применима.
3. Точность метода повышается, когда резонансная частота составного вибратора близка к собственной частоте кварцевого преобразователя. В этом случае узел колебаний попадает на место соединения образца и преобразователя. В результате влияние соединительного слоя вибратора сводится практически к нулю. Фактически достаточно совпадения 5–10 %, но это требует предварительной подгонки длины образцов [3]. Если упругие свойства материала сильно изменяются, например, в зависимости от температуры, то это может вызывать определенные неудобства при измерениях.
4. Кроме того, имеет место и обсуждается в литературе вопрос о выборе оптимальных соотношений продольных и поперечных размеров составного вибратора вследствие влияния паразитных мод колебаний. Для стержневых систем целесообразно соблюдать соотношение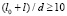 
, где l0 – длина преобразователя, l – длина образца, d – поперечные размеры преобразователя и образца.
Определенные трудности составляет расчет сдвиговых упругих постоянных по собственным частотам монокристаллических образцов с некруговым поперечным сечением. Остановимся на этом моменте подробнее.
Получение расчетных формул для анизотропных образцов с круговым и прямоугольным поперечным сечением
Для образцов в виде стержней некругового поперечного сечения и крутильных колебаний нужно учитывать поправку на депланацию поперечного сечения образцов при кручении. Поперечные сечения прямоугольной, а также любой другой некруговой формы при кручении не остаются плоскими, а искривляются по некоторой поверхности. Точки поперечного сечения перемещаются вдоль продольной оси стержня. Величина поправки для сдвиговых упругих постоянных, рассчитанных из собственных частот крутильных колебаний, определена только для поликристаллических образцов и кристаллических образцов, когда ось кручения является осью симметрии не ниже третьего порядка. Для других направлений она в литературе отсутствует.
В то же время при исследовании упругих свойств кубических монокристаллов, весьма часто приходится применять образцы ориентаций <100> и <110> квадратного или прямоугольного сечения, хотя интерпретация кручения образцов квадратного или прямоугольного сечения значительно труднее (поэтому обычно используют образцы круглого сечения). Однако технологически далеко не всегда возможно изготовить цилиндрические образцы с круглым поперечным сечением.
Собственная частота крутильных колебаний стержня [4]
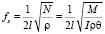, (2)
где N – динамическая упругая постоянная кручения,
M – статический вращающий момент,
I – момент инерции сечения на единицу длины стержня,
ρ – плотность материала стержня,
θ – деформация кручения.
Расчет, таким образом, сводится к нахождению надлежащего выражения для M = M(θ). Показано, что для анизотропного стержня с ребрами a < b (рис. 2)
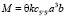, (3)
где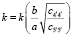 
– табулированный Сен-Венаном коэффициент.
Таблица для его определения приведена в многочисленных источниках, например по сопротивлению материалов. Фрагмент таблицы приведен в таблице.
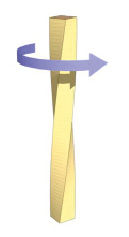
Рис. 2. Кручение образца прямоугольного поперечного сечения
Фрагмент таблицы
|
b/a |
k |
|
1 |
0,1406 |
|
1,2 |
0,166 |
|
1,5 |
0,196 |
|
2 |
0,229 |
|
2,5 |
0,249 |
|
3 |
0,263 |
|
4 |
0,281 |
|
5 |
0,291 |
|
10 |
0,312 |
|
∞ |
0,333 |
Момент инерции сечения на единицу длины стержня можно найти по формуле
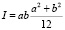. (4)
Компоненты тензора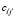 
– это упругие постоянные в системе координат, связанной с образцом. Ось 
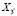направлена вдоль оси образца, ос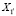и 
и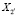 
занимают любое из двух возможных направлений в плоскости, нормальной к 
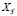. Штрихи здесь, как и в предыдущих формулах, показывают, что данные компоненты тензора упругих постоянных отнесены не к кристаллографической, а к специальной декартовой системе координат, связанной с образцом и отличной, вообще говоря, от кристаллографической. Как и подобает, штрихи помещены над индексами [5].
В результате из (2) получаем
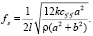(5)
Данная формула является устанавливающей для расчета ряда упругих постоянных монокристаллических образцов с прямоугольным поперечным сечением и имеет для нас важные следствия.
Для стержня квадратного сечения с ребром a статический вращающий момент
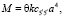(6)
где 
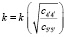и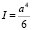 
, а его собственная частота
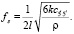(7)
Проанализируем два варианта применения образцов призматической формы с ориентацией продольной оси относительно кристаллической структуры.
1. Для образцов кубической системы, ориентированных по оси куба <100>,
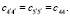(8)
Отсюда модуль с44 может быть вычислен из формулы
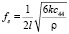, (9)
где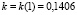 
. Соотношение (9) эквивалентно формулам для модуля сдвига поликристаллических и монокристаллических образцов прямоугольного поперечного сечения
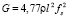(10)
(эту формулу можно видеть в литературе) и
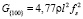(11)
что также согласуется с литературными данными. Как известно, упругая постоянная с44 определяет для кубических кристаллов сопротивление сдвигу плоскости {100} в направлении, лежащем в этой плоскости.
2. Выделить в «чистом виде» кручением С' нельзя. Для образцов с осью вдоль направления <110>, которое может служить для определения С', целесообразно использовать боковую огранку образцов {100} и {110}. В этом случае
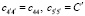(12)
и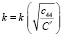 
, откуда
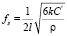. (13)
Из (13) величина С' может быть найдена, хотя и численными методами, поскольку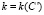 
. Напомним, что линейная комбинация упругих постоянных 
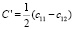в кристаллах кубической системы контролирует сопротивление так называемому «зинеровскому» сдвигу – сдвигу плоскости {110} в направлениях 
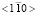. Смягчение этой постоянной может привести к ряду структурных фазовых превращений в твердых телах с изменением типа кристаллической решетки, например B2–B19 в сплавах TiNi с памятью формы [6].
Заключение
Рассмотрены особенности применения метода составного ультразвукового вибратора при измерении упругих характеристик и внутреннего трения твердых тел. Получены выражения для вычисления сдвиговых упругих постоянных кубических кристаллов с44 и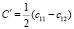 
по измеренным значениям резонансных частот крутильных колебаний образцов с квадратным или прямоугольным поперечным сечением в методе составного пьезоэлектрического вибратора для материалов кубической сингонии. Наиболее простые формулы имеют место для постоянной с44. Для определения 
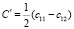необходимо применение численных вычислительных методов или специализированных программ, например Mathcad.