Влияние, оказываемое человеком на водные ресурсы, подвергает экосистему водоема значительным изменениям, например, меняется температурный режим водоема, режим уровня воды, гидрохимический режим и др. В связи с этим необходим мониторинг состояния водных объектов, а также прогнозирование возможных чрезвычайных ситуаций, связанных с заморными явлениями, поднятием уровня воды и затоплением прибрежных районов, что позволит спасти человеческие жизни и сократить наносимый материальный ущерб.
При моделировании процессов, происходящих в мелководных водоемах, классическими являются модели, основанные на уравнениях Навье – Стокса (уравнениях параболического типа) [1]. Аппроксимация такой модели с помощью неявных схем обладает достаточным запасом устойчивости и налагает обременительные ограничения на шаг по времени как в случае явной схемы. В ряде работ [2–4] удалось ослабить это ограничение за счет гиперболизации уравнений модели. Кроме того, в случае большого числа узлов расчетной сетки такая гиперболизированная явная схема оказывается вычислительно более выгодной при параллельной программной реализации благодаря сокращению количества передач данных при решении системы линейных алгебраических уравнений (СЛАУ).
Формулировка непрерывной модели
В работе [5] была рассмотрена модель гидродинамики мелководных водоемов с уточненными граничными условиями. Недостатком описанной модели, в основе которой лежат уравнения параболического типа, является то, что в отличие от реально протекающего процесса, модель не способна описывать распространение значений физических величин (таких как скорость движения среды, давление и др.) с конечной скоростью. Данный недостаток отсутствует в уравнениях гиперболического типа, при этом формируется фронт волны, скорость движения которого зависит от коэффициента при второй производной по времени, а сама вторая производная принимается в качестве регуляризирующего слагаемого, сглаживающего решение и позволяющего ослабить ограничения на шаг по времени [6].
Распространение возмущений в водоеме возможно благодаря сжимаемости жидкости (зависимость плотности от давления), поэтому полагаем
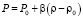 , (1)
, (1)
где β – коэффициент сжимаемости жидкости (для воды 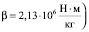 .
.
С учетом (1) система гиперболизированных уравнений движения имеет вид
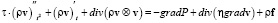 , (2)
, (2)
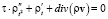 , (3)
, (3)
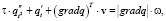 (4)
(4)
где τ – регуляризирующий параметр, определяющий время между взаимодействиями, по порядку равное времени, за которое акустическая волна проходит ячейку расчетной сетки [7]:
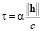 , (5)
, (5)
где c – скорость звука в воде, 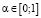 – безразмерный параметр.
– безразмерный параметр.
Граничное условие для давления на свободной границе для уравнений (2)–(4) имеет вид
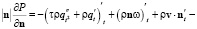
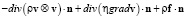 . (6)
. (6)
Дискретизация
При расщеплении по физическим процессам система (2)–(4) примет вид
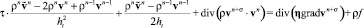 ,
,
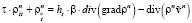 ,
,
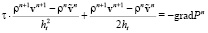 .
.
Граничное условие (6) примет вид
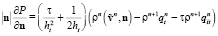 .
.
Аппроксимация по пространственным направлениям выполнена с помощью интегро-интерполяционного метода с частичной заполненностью [6]. Условия устойчивости полученной разностной схемы:
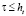 ,
, 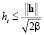 ,
, 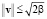 ,
,
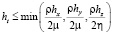 ,
, 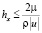 ,
,
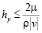 ,
, 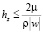 .
.
Оценим величину шага по времени, допустимого при решении практических задач. Примем  м,
м, 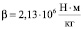 , тогда
, тогда 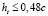 .
.
Аналитическое сравнение вычислительной сложности алгоритмов
Выполним оценку количества полных проходов по узлам расчетной сетки, необходимого для получения решения в конкретный момент времени для алгоритмов на основе классических уравнений Навье – Стокса и системы гиперболизированных уравнений гидродинамики. Пусть размер сетки N1× N2×N3, размер расчетной области l1×l2×l3, u, v, w – три компоненты поля скорости.
Предположим, что решение необходимо получить в момент времени 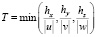 . В случае неявной схемы это означает, что нужно выполнить только один шаг по времени и решить уравнения типа диффузии-конвекции-реакции. При использовании попеременно-треугольного метода (ПТМ) количество внутренних шагов по времени асимптотически пропорционально максимальному числу узлов сетки по одному из направлений [8]. Учтем также, что в нашем случае эта константа пропорциональна отношению шага расчетной сетки по горизонтальному направлению к шагу по вертикальному направлению. Таким образом, количество шагов ПТМ совместно с методами сопряженных и бисопряженных направлений асимптотически равно [9]
. В случае неявной схемы это означает, что нужно выполнить только один шаг по времени и решить уравнения типа диффузии-конвекции-реакции. При использовании попеременно-треугольного метода (ПТМ) количество внутренних шагов по времени асимптотически пропорционально максимальному числу узлов сетки по одному из направлений [8]. Учтем также, что в нашем случае эта константа пропорциональна отношению шага расчетной сетки по горизонтальному направлению к шагу по вертикальному направлению. Таким образом, количество шагов ПТМ совместно с методами сопряженных и бисопряженных направлений асимптотически равно [9] 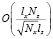 .
.
При численном решении задач гидродинамики мелководных водоемов на основе трехмерной системы уравнений Навье – Стокса ограничение на шаг по времени определяется вертикальными составляющими скорости и шага по пространству. В случае применения модели на основе гиперболизированной системы уравнений гидродинамики, количество шагов по времени, требуемых для получения решения в момент времени T асимптотически равно 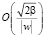 .
.
Из всего вышесказанного можно заключить, что применение модели на основе системы гиперболизированных уравнений более предпочтительно при выполнении условия
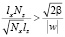 . (7)
. (7)
где 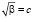 – скорость звука в воде.
– скорость звука в воде.
В случае Азовского моря lx = 380000 м, lz = 17 м, характерная вертикальная скорость w = 0,01 м, тогда модель на основе гиперболизированных уравнений вычислительно более эффективна по сравнению с моделью на основе уравнений Навье – Стокса параболического типа при 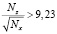 . Такое соотношение количества узлов расчетной сетки вполне достижимо, то есть оба метода обладают примерно одинаковой применимостью. Далее будет показано, что на практике параллельная реализация метода на основе гиперболизированных уравнений позволяет получить значительно более эффективный алгоритм расчета модели.
. Такое соотношение количества узлов расчетной сетки вполне достижимо, то есть оба метода обладают примерно одинаковой применимостью. Далее будет показано, что на практике параллельная реализация метода на основе гиперболизированных уравнений позволяет получить значительно более эффективный алгоритм расчета модели.
Численные эксперименты
Проверку адекватности построенной модели на основе гиперболизированных уравнений реально протекающему физическому процессу, а также сравнение прогнозируемых гидродинамических параметров и быстродействие разработанных алгоритмов прогнозирования на основе классических (параболических) и гиперболизированных уравнений Навье – Стокса выполним на основе данных о затоплении прибрежных регионов Азовского моря из-за штормового нагона, которое произошло 24–25 сентября 2014 г. в районе порта г. Таганрога. Скорость и направление ветра приведены в таблице [9].
Данные о скорости, направлении ветра и уровне воды в районе порта г. Таганрога, 24–25 сентября 2014 г.
|
Момент времени |
24 сентября 2014 |
25 сентября 2014 |
|||||||
|
00:00 |
04:00 |
08:00 |
12:00 |
16:00 |
20:00 |
00:00 |
04:00 |
08:00 |
|
|
Направление ветра |
Ю-В |
Ю-В |
Ю |
Ю-Ю-З |
Ю-Ю-З |
З |
Ю-З |
Ю-З |
Ю-З |
|
Скорость ветра, м/с |
17 |
18 |
27 |
33 |
37 |
33 |
28 |
22 |
18 |
|
Уровень воды, см |
12 |
24 |
66 |
160 |
380 |
420 |
390 |
320 |
280 |
Результаты численного моделирования представлены на рис. 1. В качестве начального приближения использовались результаты расчета течений в Азовском море в условиях отсутствия ветра. При численном моделировании нагонных явлений предполагалось, что возрастание скорости ветра 24 сентября 2014 г. от 0 м/с до 17 м/с (первый столбец таблицы) происходило линейным образом в течение 5 часов. Из графиков на рис. 1 видно, что результаты расчетов на грубой сетке достаточно точно повторяют результаты, полученные на подробной сетке, а значения функции возвышения уровня располагаются достаточно близко по отношению к наблюдаемым значениям.
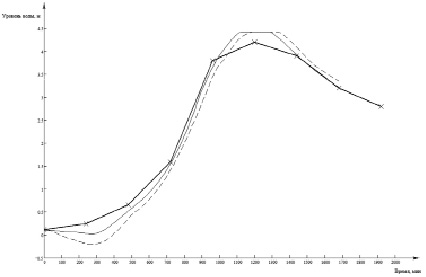
Рис. 1. Функция возвышения уровня в районе порта г. Таганрога (пунктирная линия – значения, рассчитанные на сетке с шагами по горизонтальным направлениям – 1003 м и 1013 м, тонкая линия – значения, рассчитанные на сетке с шагами по горизонтальным направлениям – 503 м и 510 м; шаг сетки по вертикальному направлению – 0,1 м; ломаная линия – натурные данные)
Также выполнена программная реализация математической модели гидродинамики и сгонно-нагонных явлений в мелководных водоемах на основе регуляризированных уравнений Навье – Стокса на параллельной вычислительной системе с общей памятью с помощью библиотеки OpenMP [9]. Зависимость ускорения от количества процессоров представлена на рис. 2, а эффективности – на рис. 3.
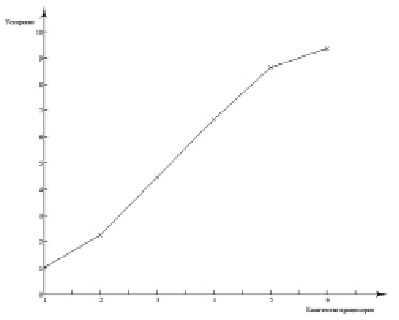
Рис. 2. Ускорение параллельной программы
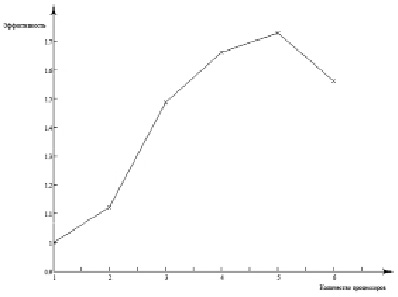
Рис. 3. Эффективность параллельной программы
По полученным результатам (рис. 3) видно, что эффективность параллельной программы больше единицы, то есть программа показывает суперлинейное ускорение из-за независимости вычислений в рамках итерации по времени, при этом барьерная синхронизация – единственный дополнительный расход. Высокая эффективность параллельной реализации достигается благодаря следующим особенностям алгоритма:
1. Явная схема расчета позволяет значительно сократить число синхронизаций параллельных потоков;
2. Использование нового метода для моделирования свободной поверхности позволяет избежать дополнительных временных расходов на перестройку расчетной сетки области.
3. Применение интегро-интерполяционного метода с частичной заполненностью позволило использовать структурированные регулярные сетки и регулярные структуры данных для их хранения, что повышает эффективность работы КЭШ-памяти процессора.
Выводы
В работе рассмотрена математическая модель гидродинамики со свободной поверхностью и изменяемой геометрией береговой линии на основе гиперболизированных уравнений Навье – Стокса. Введение регуляризирующего параметра τ позволяет увеличить шаг по времени при численном решении уравнений с помощью явных схем и повысить эффективность параллельной программной реализации алгоритма по сравнению с моделью на основе классических уравнений (уравнений параболического типа) Навье – Стокса.
Проведено аналитическое сравнение вычислительной сложности алгоритмов на основе классических уравнений Навье – Стокса и системы гиперболизированных уравнений. Показано, что при выполнении условия (7) гиперболизированная модель гидродинамики вычислительно предпочтительнее классической модели на основе уравнений Навье – Стокса параболического типа. Другими словами, классическая модель предпочтительнее при малой скорости течений и грубой расчетной сетке, а при увеличении количества узлов сетки (при измельчении сетки) или при возрастании скорости течений лучше использовать регуляризированную модель.
Выполнена программная реализация модели на основе гиперболизированных уравнений гидродинамики на параллельной вычислительной системе с общей памятью с использованием библиотеки OpenMP и приведены графики ускорения и эффективности параллельной программы в зависимости от количества процессоров.
Работа выполнена при финансовой поддержке РФФИ по проекту № 15-07-08408.

