Возникновение потенциала действия нейрона (состояние возбуждения нейрона) обычно трактуется как результат воздействия внешнего стимула. Частота следования потенциалов действия (ПД) первых (после рецепторов) нейронов имеет значение 30–5000 имп/с.
Однако, даже в отсутствии внешних стимулов нейроны ряда областей мозга проявляют спонтанную активность. В случае ганглиозных клеток (зрительная система) частота спонтанной активности этих клеток при отсутствии светового сигнала колеблется в пределах 2–20 имп/с. [1].
В нейронах кохлеарного ядра (слуховая система) спонтанная активность (при отсутствии звукового сигнала) имеет значение 2–30 имп/с. [2]. Спонтанная активность нейронов проявляется и когда они находятся в изолированном состоянии, её величина равна 1–2 имп/с. [3]. Во всех приведенных случаях система, содержащая нейрон, находится в состоянии термодинамического равновесия. Что является стимулом (спусковым механизмом) возникновения спонтанного ПД? Учитывая состояние термодинамического равновесия системы, ряд факторов, традиционно связываемых с возникновением ПД, необходимо исключить. Это активизация ионных каналов, включение (выключение) ионных насосов и др. [4].
Первоначальным стимулом (спусковым механизмом) активизации ПД может быть фазовый переход липидной мембраны при условии, что в состоянии термодинамического равновесия она находится в высокотемпературной (жидкокристаллической) фазе и под действием оптических фононов (веерные колебания полярных «головок») переходит в низкотемпературную (гель) фазу. Этот переход осуществляется в результате того, что оптические фононы веерных колебаний полярных «головок» липидов, структурированных в мембране, изменяют напряжённость электростатического поля мембраны.
Как известно [5–7], фазовый переход в неорганических и органических кристаллах из высокотемпературной фазы в низкотемпературную фазу (при постоянной температуре) совершается при приложении электрического поля, если кристалл находится при температуре выше точки фазового перехода на 1–5 °С в случае неорганических кристаллов [6–7] и на 2–10 °С в случае органических кристаллов [5]. Этот переход происходит в том числе, когда отмеченные кристаллы имеют наноразмерные толщины [8]. Напряжённость электрического поля, вызывающего этот фазовый переход, составляет 104–106 В/м. Фазовый переход можно считать спусковым механизмом (первой фазой) ПД. Последующая (во времени) структура ПД связана с активизацией ионных каналов, включением ионных насосов… и, конечно, с возвращением мембраны в термодинамическое равновесие, т.е. в жидкокристаллическую фазу.
В работе [9] рассмотрены оптические фононы модельной мембраны, представляющей собой сферу. Возьмём за основу эту же структуру мембраны нейрона, ориентация молекул в которой определяется двойным липидным слоем (≈70 % массы липидной мембраны).
Липидные молекулы могут находится в двух конформационных состояниях. Как и в [9], считаем, что эти два конформационных состояния определяются двумя основными электронными состояниями (i = 1,2) молекул Φi,j = φi (r, R0)∙ψi,j(Qj), (где r и R – совокупность координат электронов и ядер), вероятность перехода между которыми мала. В адиабатическом приближении энергии этих состояний равны Ei,j = Eiэл (r, R0) + ,Еiкj (Qj), где R0 – равновесная конфигурация ядер, Qj – обобщённые колебательные координаты молекул; ¦Еiэл (r, R0 )¦>> ¦EiкJ (Qj)¦, Eiкj – колебательная энергия.
1. Рассмотрим сначала колебания изолированной молекулы фосфолипида на примере фосфатидилхолина. Молекула находится в конформационном состоянии с более высокой энергией i = 1. На рис. 1 представлена структурная схема этой молекулы. Ориентацию (α0) полярной «головки» относительно гидрофобного «хвоста» фосфатидилхолина возьмём такую же, которую она имеет в мембране α0 ≈ 300. Из всех колебаний изолированной молекулы (3N-6) (N – число атомов в молекуле) рассмотрим веерные колебания полярной «головки» относительно гидрофобного «хвоста». Энергии квантов валентных и деформационных колебаний имеют значения 3500–400 см-1. Энергия квантов веерных колебаний больших фрагментов молекул равна 50–150 см-1. Возьмём значение кванта энергии веерного колебания полярной «головки» фосфатидилхолина равным 100 см-1.
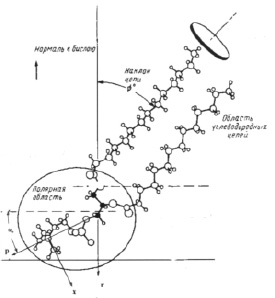
Рис. 1. Структура молекулы фосфатидилхолина; р – дипольный момент полярной «головки» молекулы
Структурное положение полярной «головки» в молекуле фосфатидилхолина (рис. 1) определяет асимметрию веерных колебаний (асимметрию потенциальной энергии U = f(α)). В работе [9] потенциальная энергия взята в форме U = [α4 + U0 exp[ – 2(α + 1)2]. Именно асимметрия веерных колебаний полярных «головок» должна обуславливать изменение ориентации (α) диполя «головок» при изменении температуры.
Поскольку энергия кванта веерных колебаний hν = 100 cm-1(hν(Дж)/hc) существенно меньше средней энергии теплового движения частиц ɛ = kT = 4,28·10-21 Дж (217 см-1) при Т = 315 °К, необходимо определить волновые функции и энергии колебательных уровней значительного числа возбуждённых состояний. Для их определения возьмём асимметричный ангармонический потенциал в более простой форме в сравнении с потенциалом работы [9], а именно:
U = (1/2·ε2 + β·ε3). (1)
Уравнение Шредингера для стационарных состояний такого ангармонического осциллятора имеет вид
--1/2·d2 ψ/dε2 + (1/2·ε2 + β·ε3)∙ψ = E∙ψ, (2)
где β – малый поправочный член, возьмём β = 0,03; ε = х/x0 (рис. 1),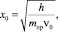 
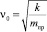– собственная частота гармонического осциллятора (β = 0);
mпр – приведенная масса полярной «головки»; x = d·sinα, d – плечо диполя полярной «головки».
Собственные функции ангармонического осциллятора (2) в первом приближении определяются выражением [10]:
ψn = ψn0 + β·ψ'n , (3)
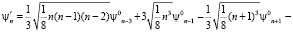
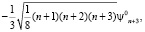
где ψn0 – собственные функции гармонического осциллятора (β = 0).
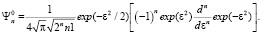(4)
Собственные значения энергий стационарных состояний осциллятора (2) во втором приближении равны
En = En0 + β2 ·E'n = h·ν0 [(n + 1/2) – 15/4·β2∙(n2 + n + 11/30)],, (5)
где n = 0,1, 2,…
Волновые функции и энергии основного и первых возбуждённых колебательных состояний молекулы фосфатидилхолина определяются соотношениями
ψ1,0 = [0,75 – 0,0224 ε – 0,0075 ε3]·exp(–ε2/2),
ψ1,1 = [0,0543 + 1,06 ε – 0,122 ε2 – 0,0089 ε4]·exp(–ε2/2),…
. (6)
.
.
Ψ1,6 = [– 0,48 + 0,318ε + 2,52ε2 – 1,23ε3 – 1,68ε4 +0,75ε5 + 0,224ε6 –
– 0,107 ε7 + 0,00205ε9]∙exp(–ε2/2);
Е1,0 = 49,87 см-1; Е1,1 = 149,20см-1; Е1,2 = 248,19 см-1 ,…Е1,6 = 635,71 см-1.
Величина дипольного момента полярных головок фосфолипидов находится в пределах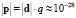 
Кл•м. Для фосфатидилхолина возьмём величину дипольного момента, принятую в работе [11] ¦p¦ = 0,6•10-9 м•1,6•10-19 Кл = 0,96•10-28 Кл•м. Асимметричность потенциальной энергии рассматриваемого осциллятора (1) обуславливает асимметричность волновых функций, изменение радиальной составляющей дипольного момента полярной «головки» и радиальной координаты (параллельной радиальному направлению мембраны) положительного иона диполя Δr = xср соsα0 (xср – среднее значение положения (рис. 1) иона диполя при изменении температуры):
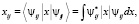(7)
где Nj – заселённость j-го колебательного уровня осциллятора при заданной температуре.
Nj = N0·exp(Ej/kT). (8)
При температуре Т = 315 °К имеем: N1 = N0·0,633, N2 = N0·0,4016,... N6 = N0·0,067. Ограничение рассматриваемых энергетических состояний j ≤ 6 даёт погрешность при определении хср не более 15 % , хср = 0,00196 нм.
Асимметричность веерного колебания полярной «головки» фосфолипидов (хср ≠ 0) определяет величину изменения радиальной составляющей дипольного момента полярной «головки» (Δp = Δr∙q).
2. Рассмотрим ряд параметров системы взаимодействующих молекул фосфолипидов, образующих сферическую мембрану. Одним из таких параметров является напряжённость электростатического поля внутри бимолекулярного слоя и в пространстве, прилегающем к этому слою (рис. 2).
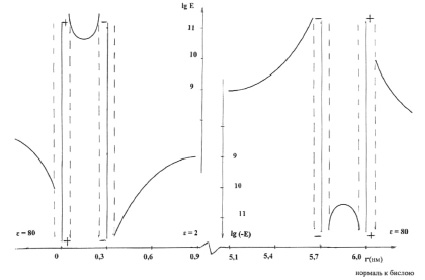
Рис. 2. Напряжённость электростатического поля бимолекулярного слоя модельной мембраны
Напряжённость электростатического поля определим в пространстве, удалённом от полярных «головок» молекул не более чем на 3 нм. При нахождении величины напряжённости электростатического поля в каждой точке обозначенного пространства учитываем влияние ближайших (к данной точке) 1000 ионов. Благодаря экранирующему действию цитоплазмы сомы нейрона (ε = 80), погрешность, возникающая при таком ограничении, не превышает 10 %.
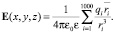(9)
В пределах пространства каждого иона, диаметр которых принят равным 0,1 нм, напряжённость поля не рассматривается. На рис. 2 представлена радиальная зависимость величины напряжённости электростатического поля; расстояние между соседними отрицательными ионами 0,4 нм, α0 = 300, плечо диполя d = 0,6 нм (рис. 1), заряды ионов q = ± 1,6·10-19 Кл.
При изменении температуры мембраны изменяется заселённость энергетических уровней осцилляторов веерного типа полярных «головок» фосфолипидов. Вследствие асимметричности этого колебания меняется радиальная составляющая дипольного момента (Δp = Δr∙q) полярных «головок» молекул и изменяется напряжённость электростатического поля в окружающем пространстве.
Возьмём температуру термостата, в котором находится нейрон (независимо от природы термостата) равной Т = 315 °К, температуру фазового перехода «жидкий кристалл – гель» равной 310 °К. При нагревании мембраны нейрона от 310 °К до 315 °К появляется дополнительное электростатическое поле ΔЕ. Средняя величина этого поля, определяемая изменением радиальной составляющей диполя полярной «головки» (Δр = xcp·cosα0 ·q), в пространстве бислоя мембраны составляет ≈1 % от величины электростатического поля, представленного на рис. 2, т.е. в пределах бислоя мембраны ΔЕ = 104 –107 В/м. Для жидкого кристалла (мембраны), находящегося при температуре 315 °К близкой к температуре фазового перехода (310 °К), напряжённости этого поля достаточно, чтобы перевести кристалл из высокотемпературной фазы в низкотемпературную. При этом фазовом переходе молекулы фосфолипидов переходят из одного конформационного состояния (Ф1,j) в другое (Ф2,j), изменяя свою структуру, а также геометрию электронного облака.
3. Взаимодействие диполей полярных «головок» липидов в мембране приводит к образованию из каждого энергетического уровня веерных осцилляторов энергетической зоны. Оператор диполь-дипольного взаимодействия имеет вид
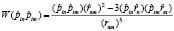, (10)
где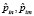 
– операторы дипольных моментов ангармонических осцилляторов n и m (m = n ± 1), 
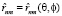– радиус вектор, θ и φ – сферические углы, задающие положение осцилляторов в мембране.
Гамильтониан системы N осцилляторов мембраны с учётом диполь-дипольного взаимодейтвия ближайших соседей можно записать:
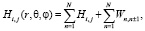(11)
где Hi,j – гамильтониан изолированной молекулы, находящейся в состоянии i (i = 1,2).
Учитывая трансляционную симметрию мембранной структуры, волновую функцию, соответствующую оператору Гамильтона (11), можно представить (в нулевом приближении) в виде
Ψijq(θ, φ) =N-1/2Σn Ψij(θ + nθo, φ + nφо) exp(iqn),(12)
где Ψij – волновые функции изолированных молекул, q = (2πn1/N1θo + 2πn2/N2φо) – волновой вектор, N1N2 = N; θo = 2π/N1 , φо = 2π/N2 (θo = φо = 2π α /2πRo ≈ 2∙10-5рад, R0 – радиус мембраны, α ≈ 0,4 нм – расстояние между соседними молекулами).
При малом перекрывании волновых функций соседних молекул получим выражение для собственных значений гамильтониана:
Еijq = Еij + 2•J•cos(q(θ, φ)), (13)
J = ∫Ψ*ij(θ, φ)∙Wn,n±1∙Ψij(θ, φ) dθ dφ
где Еi,j – собственные значения гамильтониана изолированных молекул фосфолипидов.
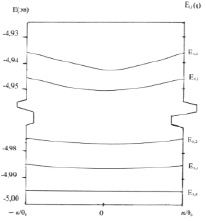
Рис. 3. Зонная структура фононных состояний i = 1, j = 0,1,2…6 модельной мембраны, образованной молекулами фосфатидилхолина. Энергия колебательных состояний отсчитывается от основного электронного состояния, величина которого принята равной (–5 эв = 5000 см-1)
На рис. 3 представлена схема энергетических зон, образованных из колебательных уровней j = 0, 1, 2, … 6 полярных «головок» молекул фосфолипидов, находящихся в электронном состоянии i = 1. Энергия колебательных уровней отсчитывается от основного электронного состояния молекулы фосфолипида, величина которого принята равной (–5 эв = –5000 см-1) – типичная для органических молекул типа фосфолипидов [12].
Подобную схему энергетических зон Еi,j,q можно представить и для мембраны из молекул фосфолипидов, находящихся в конформационном состоянии i = 2 (низкотемпературная фаза).
Заключение
Фазовый переход мембраны из высокотемпературной жидкокристаллической фазы в низкотемпературную гель фазу под действием электростатического поля веерных колебаний полярных «головок» фосфолипидов должен сопровождаться квантовыми переходами между зонами, так как энергетические зоны этих двух фаз при одинаковой температуре должны иметь разную заселённость.