В [1] Ф. Розенбергер справедливо пишет, что за всю историю физики господствующее воззрение на сущность силы являлось истинным руководящим началом в развитии физики, и представление о действии силы давало решающее направление работам физиков. Воззрения на сущность сил электромагнитной природы воплощаются в концепциях света и вообще электромагнитных волн. Изначально имели право на существование следующие концепции:
1) полевая (свет есть волна в материальном электромагнитном поле; скорость света в физической среде складывается со скоростью этой среды и не зависит от скорости источника, так что среда полностью увлекает поле);
2) эфирная (свет есть волна в материальном светоносном эфире; скорость света в физической среде складывается со скоростью эфира, а эфир частично увлекается средой);
3) эмиссионная или, иначе, баллистическая (свет есть материальное истечение вещества; скорость света в физической среде складывается со скоростью источника);
4) мгновенного дальнодействия (свет нематериален; скорость света в физической среде бесконечна; сила действует непосредственно через пространство);
5) запаздывающего дальнодействия (свет нематериален; скорость света в физической среде складывается со скоростью источника, как в эмиссионной концепции; сила действует непосредственно не только через пространство, но и через время).
Современная классическая теория электромагнитного поля, основанная на уравнениях Максвелла и постулате о силе Лоренца, сложилась в результате победы первой концепции над остальными тремя, а квантовая электродинамика и электродинамика сплошных сред явились дальнейшей реализацией и распространением той же самой полевой концепции. В отличие от эфирной и эмиссионной концепций, которые естественным образом математически формализуются в рамках классических представлений о пространстве и времени, полевая концепция требует отказа от них. Математической моделью пространства и времени в полевой концепции естественным образом служит пространство-время Минковского специальной теории относительности (релятивистские представления о пространстве и времени). В итоге все современные теории электромагнетизма сложились в релятивистскую электродинамику, в которой сущность сил электромагнитной природы усматривается в представлениях об электромагнитном поле в пространстве-времени Минковского.
Имевшее место развитие релятивистской электродинамики увенчалось значительными и несомненными достижениями, но дальнейшее её развитие наталкивается на принципиальные трудности, что делает актуальной проработку вопроса о возможной целесообразности пересмотра её фундаментальных основ – полевой концепции и релятивистских представлений о пространстве и времени. Такую проработку целесообразно начать с простейшего частного случая, который допускает последующее естественное и всеобъемлющее обобщение. Так как произвольная система зарядов, включая материальную среду её движения, принципиально может быть разложена на конечную совокупность заряженных материальных точек (ЗМТ), движущихся в абсолютном вакууме, то таким частным случаем является случай ЗМТ.
Целью данной статьи является разработка на новой концептуальной основе в рамках новых представлений о пространстве и времени единой математической модели сил электромагнитной природы, создаваемых в вакууме движущейся ЗМТ, и инертности её движения.
Развитие математики в последние десятилетия выявило принципиальную теоретическую внутреннюю противоречивость релятивистских представлений (теорема Л. Келдыш об открытом отображении в компакт; преобразования Лоренца образуют не группу преобразований в строгом смысле, а лишь частичный группоид; недоказанность единственности преобразований Лоренца в классе эквиаффинных преобразований; недостижимость установления симметрий ускоренного движения и выявления их связи с симметриями неускоренных движений на пути обобщения преобразований Лоренца; недоказуемость принципа локальности и установление неоднозначности разрешения парадокса близнецов при анализе этого принципа; недоказуемость принципа относительности одновременности) [2], а также их контрадикцию уравнениям Максвелла [3]. Среди многочисленных публикаций ряда учёных, содержащих справедливую критику этих представлений, отметим ещё работы [4, 5]. Опыты Маринова по измерению разности световых скоростей в двух противоположных направлениях [6] противоречат релятивистскому постулату о постоянстве скорости света. Результаты многочисленных экспериментов с интерферометрами нельзя считать подтверждающими этот постулат ввиду использования в них неподходящих интерферометров [7, 8]. В релятивистской электродинамике обнаружен ряд теоретических парадоксов [9], а обширные экспериментальные данные, в частности опыты Фарадея, Эдвардса, Кеньёна, Лемона, Николаева, Cигалова, Грано, Околотина, Румянцева, Окулова, Солунина, Костина, Фефелова, Родина, Черникова [9, 10], выявили её принципиальное несовершенство.
Указанные проблемы ставят под сомнение справедливость полевой концепции и возвращают к поиску верной концепции. Наиболее убедительно опровергнутой можно считать четвёртую концепцию, так как экспериментально твёрдо установлена конечность скорости света. Самой же невероятной с точки зрения «здравого смысла» считалась пятая. Показательны слова Максвелла в его трактате [11]: «…математические выражения электродинамического действия привели Гаусса к убеждению, что теория распространения электрического действия во времени могла бы оказаться подлинным основным принципом электродинамики. Но мы не в состоянии понимать распространение во времени иначе, как только двумя способами: или как полёт материальной субстанции через пространство или как распространение состояния движения или напряжения в среде, уже существующей в пространстве. …Если нечто передаётся от одной частицы к другой на расстояние, каково состояние этого нечто после того, как оно покинуло одну частицу и ещё не достигло другой? Если это нечто есть потенциальная энергия двух частиц, как в теории Неймана, должны ли мы рассматривать эту энергию как существующую в какой-то точке пространства, не совпадающей ни с той, ни с другой частицей? Действительно, каким бы способом энергия ни передавалась от одного тела к другому во времени, должна быть среда или субстанция, в которой энергия существует после того, как она оставила одно тело и ещё не достигла другого, ибо энергия, как заметил Торричелли, «есть квинтэссенция такой тонкой природы, что она не может содержаться ни в каком другом сосуде, как только в самой сокровенной субстанции материальных вещей». …И, если мы примем эту среду в качестве гипотезы, я считаю, что она должна занимать выдающееся место в наших исследованиях и что нам следовало бы попытаться сконструировать рациональное представление о всех деталях её действия, что и было моей постоянной целью в этом трактате». В итоге в качестве реальных альтернатив господствующей полевой концепции рассматривались лишь эфирная и эмиссионная концепции.
Сотрудничество автора с высококвалифицированным харьковским физиком-экспериментатором Ф.Ф. Менде позволило получить подходящие для нахождения верной концепции экспериментальные данные в результате проведения в г. Харькове трёх классов экспериментов:
1) опыты со сверхпроводниками [12, 13];
2) опыты с плазмой [12, 13];
3) опыты с интерферометром [8].
Первые два выявили нарушение закона Гаусса. Результаты первого согласуются с результатами идейно близких опытов Эдвардса, Кеньёна и Лемона [10], второго – с результатами наблюдений электрического импульса при космических ядерных испытаниях [12, 13]. В опытах третьего использовался специально разработанный для них интерферометр нового типа (с механическим делением луча) [7], с помощью которого обнаружено постоянство во времени длины волны лазерного луча, которая не зависит от скорости движущихся по гармоническому закону генератора или зеркала. Сочетание данного нового эффекта с известным эффектом Доплера свидетельствует о классическом сложении скорости света со скоростью его источника, нарушающем принцип инвариантности скорости света теории относительности. Результаты третьего класса опытов согласуются с результатами наблюдения О. Рёмером в 1676 г. в Парижской обсерватории периодического изменения времени полного обращения спутника Ио вокруг Юпитера, определяемого по моменту выхода (или входа) спутника из тени Юпитера, которые также указывают на то, что скорость света складывается со скоростью источника [14]. Результаты третьего класса опытов противоречат полевой и эфирной концепциям, а первых двух – эмиссионной. Результаты каждого класса опытов противоречат релятивистским представлениям о пространстве и времени.
Единственная согласующаяся с этими данными и конечностью скорости света концепция – пятая. Но так ли она невероятна, как казалась? Вернёмся к трактату Максвелла [11]: «…было время, когда занимавшиеся спекуляциями о причинах физических явлений имели обыкновение объяснять каждый вид действия на расстоянии при помощи специального эфирного флюида, функцией и свойством которого было производство этих действий. Они заполняли всё пространство тремя или четырьмя перекрывавшими друг друга эфирами различных сортов. Свойства этих эфиров изобретались главным образом для того, чтобы «спасти благопристойность», так что более разумно настроенные исследователи были скорее согласны принять не только несомненный закон Ньютона о явлении притяжения на расстоянии, но даже догму Котса, что действие на расстоянии является одним из первичных свойств материи и что никакое объяснение не может быть более понятным, чем сам этот факт. Отсюда волновая теория света встретила большую оппозицию, направленную не против её неспособности объяснять явления, но против допущения существования среды, в которой свет распространяется». Лишь инерция «здравого смысла» грубого материализма мешает принять пятую концепцию, разделить понятия мгновенности действия и дальнодействия, соединить дальнодействие с запаздыванием и, следуя упомянутым разумно настроенным исследователям прошлого, расширить догму Котса с непосредственного действия только на расстоянии на непосредственное действие не только через пространство, но и через время.
Переход от полевой концепции к концепции запаздывающего дальнодействия требует перехода от релятивистских к новым представлениям о пространстве и времени, которые мы называем гиперконтинуальными [15]. В соответствии с ними пространство и время не являются самостоятельными, независимыми формами движения материи, как в классической нерелятивистской физике, а соединены в единое пространство-время, но не преобразованиями Лоренца в единый континуум, а преобразованиями Галилея в единый гиперконтинуум [12, 13]. Такие представления о пространстве и времени можно считать неоклассическими в том смысле, что они возвращают преобразованиям Галилея их фундаментальную роль. В основу гиперконтинуальной физики мы кладём четыре динамических закона сохранения: три заимствованных из классической нерелятивистской физики (законы сохранения энергии, импульса и момента импульса) и новый – закон сохранения кинетического баланса, заменяющий релятивистский закон сохранения 4-импульса. Все четыре закона связаны с соответствующими симметриями пространства-времени. Закон сохранения энергии – с однородностью времени (равноценность временных сдвигов), закон сохранения импульса – с однородностью пространства (равноценность пространственных трансляций), закон сохранения момента импульса – с изотропностью пространства (равноценность пространственных вращений). Закон сохранения кинетического баланса связан с изотропностью гиперконтинуума (равноценность изовелоцитарных, то есть сохраняющих модуль вектора скорости, преобразований Галилея).
Пересмотр фундаментальных основ означает переход от релятивистской к новой, гиперконтинуальной, электродинамике, согласно которой физически не существуют электрические, магнитные и электромагнитные поля, а в основе всех так называемых электромагнитных явлений лежит дальнодействующая электрическая сила, которая складывается из мгновенно действующей электродинамической силы (обобщающей электростатическую силу на случай движущихся зарядов) и запаздывающей электроволновой силы (описывающей так называемое электромагнитное излучение). Электрическая сила ЗМТ зависит от параметров её движения: скорости и ускорения [12, 13]. В основу гиперконтинуальной электродинамики мы кладём три закона для ЗМТ (основные законы гиперконтинуальной электродинамики):
1) закон зависимости электродинамической силы от скорости, выражающий связь между электродинамической и электростатической силами;
2) закон Кулона для электростатической силы;
3) закон зависимости электроволновой силы от ускорения.
Закон сохранения кинетического баланса служит единой причиной различия электродинамической и электростатической сил, а также динамической (гиперконтинуальная масса) и статической (обычная масса) мер инертности ЗМТ.
Задача исследования
Зададим инерциальную систему отсчета (ИСО) совокупностью часов, показывающих время 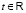 , и трехмерной системы пространственных координат. Точка наблюдения задаётся в ней постоянным во времени радиус-вектором
, и трехмерной системы пространственных координат. Точка наблюдения задаётся в ней постоянным во времени радиус-вектором 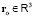 . Инвариантные параметры данной ЗМТ: масса m > 0 и электрический заряд
. Инвариантные параметры данной ЗМТ: масса m > 0 и электрический заряд 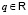 . При слиянии и разделении ЗМТ суммарные масса и заряд неизменны. Динамические параметры данной ЗМТ в момент t: радиус-вектор
. При слиянии и разделении ЗМТ суммарные масса и заряд неизменны. Динамические параметры данной ЗМТ в момент t: радиус-вектор 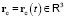 пространственного положения и вектора
пространственного положения и вектора
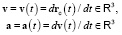
скорости и ускорения.
Динамические параметры определяют следующие характеристики положения и движения ЗМТ относительно точки наблюдения:
– вектор положения точки ro относительно ЗМТ
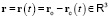 ;
;
– расстояние от ЗМТ до точки ro
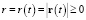 ;
;
– модуль скорости ЗМТ
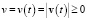 ;
;
– проекция скорости ЗМТ на направление заданного вектора X
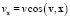 ;
;
– модуль ускорения ЗМТ
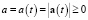 .
.
Параметры вакуума – электрическая постоянная ε0 и скорость света c. Используя дельта-функцию Дирака δ(ξ), 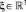 векторного аргумента ξ, плотность заряда системы «ЗМТ + вакуум» описывается функцией qδ(r(t)).
векторного аргумента ξ, плотность заряда системы «ЗМТ + вакуум» описывается функцией qδ(r(t)).
Требуется построить единую математическую модель инертности и электрической силы ЗМТ в вакууме.
Релятивистские масса 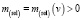 , импульс
, импульс 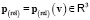 и кинетическая энергия
и кинетическая энергия 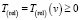 ЗМТ определяются для данной ИСО и зависят от скорости
ЗМТ определяются для данной ИСО и зависят от скорости 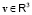 ЗМТ в ней или её модуля
ЗМТ в ней или её модуля 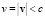 . Гиперконтинуальные масса
. Гиперконтинуальные масса 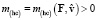 , импульс
, импульс 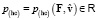 и кинетическая энергия
и кинетическая энергия 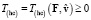 ЗМТ определяются для данной силы
ЗМТ определяются для данной силы 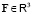 , ускоряющему действию которой противодействует инертность ЗМТ, и для данной скорости
, ускоряющему действию которой противодействует инертность ЗМТ, и для данной скорости 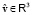 ЗМТ относительно материального источника силы F. Величины
ЗМТ относительно материального источника силы F. Величины 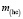 ,
, 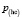 ,
, 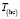 зависят от модуля
зависят от модуля 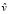 скорости
скорости 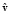 и от проекции
и от проекции 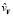 этой скорости на направление вектора F. Величины
этой скорости на направление вектора F. Величины 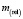 ,
, 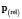 ,
, 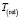 ,
, 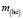 ,
, 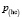 ,
, 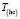 пропорциональны m.
пропорциональны m.
Сила взаимодействия двух ЗМТ пропорциональна их электрическим зарядам. При её определении всегда можно для выбранной ЗМТ из этих двух и для любого заданного момента времени t подобрать такую ИСО, в которой выбранная ЗМТ имеет в момент t нулевую скорость. Поэтому электрическую силу, создаваемую данной ЗМТ в момент t в точке ro, можно полностью характеризовать векторной величиной напряжённости этой электрической силы – электрической силой, с которой данная ЗМТ действует в момент t на пробную ЗМТ с единичным зарядом, покоящуюся в точке ro. При определении релятивистской 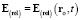 и гиперконтинуальной
и гиперконтинуальной 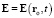 величин напряжённости удобно использовать ньютонов
величин напряжённости удобно использовать ньютонов 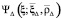 ,
, 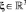 и волновой
и волновой 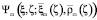 ,
, 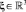 ,
, 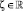 потенциалы в
потенциалы в 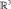 с подходящими плотностями
с подходящими плотностями 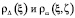 , представимыми в виде
, представимыми в виде
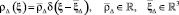 ; (1)
; (1)
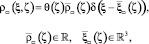 (2)
(2)
где 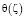 ,
, 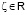 – функция Хевисайда;
– функция Хевисайда; 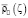 – локально интегрируемая функция в
– локально интегрируемая функция в 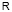 .
.
Пусть 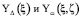 – удовлетворяющие условиям
– удовлетворяющие условиям
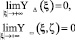
фундаментальные решения операторов в 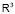 Лапласа Δ и волнового
Лапласа Δ и волнового 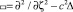 :
:
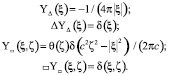 (3)
(3)
Эти ньютонов и волновой потенциалы с точностью до постоянного множителя получаются свёрткой с плотностями (1) и (2) фундаментальных решений (3):
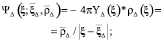 (4)
(4)
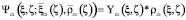 ; (5)
; (5)
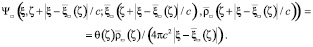 (6)
(6)
При переходе рассмотрения от ЗМТ к произвольной системе зарядов использование потенциалов (4)–(6) позволяет описать суперпозицию влияния отдельных зарядов соответствующим заданием плотности. Потенциал (6) может быть представлен потенциалом (4):
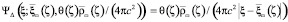 . (7)
. (7)
Одним из двух законов гиперконтинуальной электродинамики, заимствованных из релятивистской, является закон Кулона (второй закон). Согласно ему, напряжённость 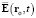 электростатической (v(t) = 0, a(t) = 0) силы с учётом (4) равна
электростатической (v(t) = 0, a(t) = 0) силы с учётом (4) равна
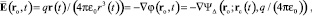 (8)
(8)
где φ(ro, t) – электростатический потенциал, возможность представления которого ньютоновым потенциалом (4) является замечательным свойством напряжённости (8).
Также заимствован из релятивистской электродинамики третий закон гиперконтинуальной, описывающий при v(t) = 0 электроволновую силу, напряжённость которой при t > 0 с учётом и без учёта диаграммы направленности излучения равна соответственно
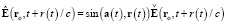 ; (9)
; (9)
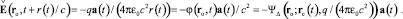 (10)
(10)
Напряжённость (10) удовлетворяет волновому уравнению
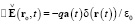 . (11)
. (11)
Формулы (9), (10) описывают электромагнитное излучение ЗМТ возмущения сферической поперечной волны (с неподвижным центром в точке rc(t)), распространяющегося со скоростью c, убывающего обратно пропорционально радиусу r(t) и возникшего в этой ЗМТ в момент времени t, когда она имела ускорение a(t) и нулевую скорость. Формула (9) выражает свойство вакуума пропускать через себя только поперечные составляющие волн общего вида 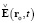 в виде поперечных волн
в виде поперечных волн 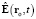 . Замечательным свойством напряжённости (10) является возможность представления её модуля волновым (6) и ньютоновым (7) потенциалами:
. Замечательным свойством напряжённости (10) является возможность представления её модуля волновым (6) и ньютоновым (7) потенциалами:
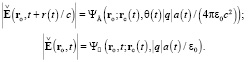 (12)
(12)
При 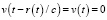 напряжённости
напряжённости 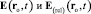 равны
равны
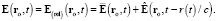 (13)
(13)
Искомая математическая модель электрической силы должна дать надлежащее обобщение равенства (13) на случай произвольной скорости.
Релятивистская математическая модель
Релятивистской динамической мерой инертности ЗМТ служит релятивистская масса
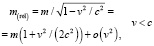 . (14)
. (14)
Релятивистский принцип относительности применительно к электромагнитному полю требует инвариантности уравнения (11) относительно скорости v(t), что распространяет область применимости формулы (10) на случай произвольной допустимой скорости 0 ≤ v(t) < c. Согласно релятивистским преобразованиям электромагнитного поля, деформация электростатического поля (8) при 0 ≤ v(t) < c описывается напряжённостью
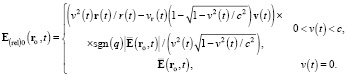 (15)
(15)
Релятивистская напряжённость 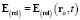 складывается из электрического поля (15) заряда ЗМТ и электрического поля (9), (10) электромагнитной волны, излучаемой ЗМТ:
складывается из электрического поля (15) заряда ЗМТ и электрического поля (9), (10) электромагнитной волны, излучаемой ЗМТ:
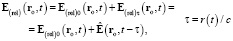 , (16)
, (16)
где 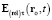 , τ ≥ 0 – напряжённость электрического поля в момент t в точке ro, обусловленная параметрами ЗМТ в момент
, τ ≥ 0 – напряжённость электрического поля в момент t в точке ro, обусловленная параметрами ЗМТ в момент 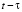 (
(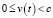 для
для 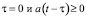 для τ > 0).
для τ > 0).
Равенство (16) есть релятивистское обобщение равенства (13) на случай 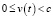 . Напряжённость (15) не может быть представлена в виде
. Напряжённость (15) не может быть представлена в виде 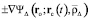 с подходящим значением параметра
с подходящим значением параметра 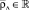 подобно электростатической силе (8). Из (15) имеем
подобно электростатической силе (8). Из (15) имеем
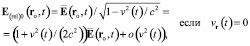 ; (17)
; (17)
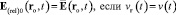 . (18)
. (18)
Согласно закону Гаусса релятивистской электродинамики поток вектора 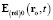 напряжённости электрической силы через любую замкнутую поверхность Ω, заключающую внутри себя ЗМТ, равен инвариантной относительно скорости величине
напряжённости электрической силы через любую замкнутую поверхность Ω, заключающую внутри себя ЗМТ, равен инвариантной относительно скорости величине
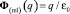 .
.
Рост нормальных компонент (17) напряжённости (15) с ростом скорости v(t) компенсируется релятивистским эффектом Лоренцева сокращения.
Гиперконтинуальная математическая модель
Гиперконтинуальный аналог классического и релятивистского разложения полной энергии в сумму кинетической и потенциальной – разложение
W = U + V
гиперконтинуальной полной энергии W ≥ 0 в сумму потенциальной энергии U ≥ 0 и точки кинетического баланса
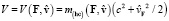 . (19)
. (19)
Закон сохранения кинетического баланса означает, что величина (19) не зависит от F:
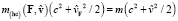 . (20)
. (20)
С одной стороны, величина V равна сумме обычной (релятивистской) энергии покоя
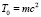
и обычной (классической) кинетической энергии
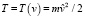
относительно материального источника силы, с другой – сумме гиперконтинуальной энергии покоя 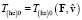 и гиперконтинуальной кинетической энергии
и гиперконтинуальной кинетической энергии 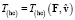 :
:
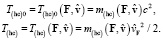 (21)
(21)
Из (20) имеем
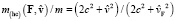 . (22)
. (22)
При 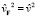 (случай
(случай 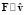 ) из (21), (22) имеем
) из (21), (22) имеем
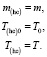
Рост величины (22) с ростом угла между 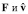 от 0 до π/2 компенсирует уменьшение величины
от 0 до π/2 компенсирует уменьшение величины 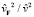 , поддерживая некий общий баланс (закон сохранения кинетического баланса). При
, поддерживая некий общий баланс (закон сохранения кинетического баланса). При 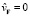 (случай
(случай 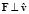 ) величина (22) максимальна, и величина
) величина (22) максимальна, и величина 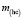 есть поперечная масса
есть поперечная масса
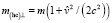 . (23)
. (23)
При 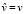 величины (14) и (23) совпадают с точностью до квадратичного члена разложения в степенной ряд по скорости.
величины (14) и (23) совпадают с точностью до квадратичного члена разложения в степенной ряд по скорости.
В отличие от релятивистского, гиперконтинуальный импульс
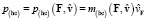 (24)
(24)
для конкретных величин F, 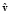 является не векторной, а числовой величиной. При
является не векторной, а числовой величиной. При 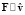 гиперконтинуальный импульс (24) равен модулю
гиперконтинуальный импульс (24) равен модулю 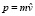 обычного (классического) импульса
обычного (классического) импульса 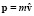 относительно материального источника силы F.
относительно материального источника силы F.
Учитывающий относительность инертности гиперконтинуальный второй закон Ньютона для обретающей ускорение 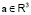 под действием силы
под действием силы 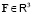 ЗМТ массой
ЗМТ массой 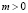 , имеющей модуль
, имеющей модуль 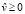 скорости движения относительно материального источника силы и проекцию
скорости движения относительно материального источника силы и проекцию 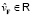 этой скорости на направление вектора F, имеет вид
этой скорости на направление вектора F, имеет вид
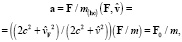 (25)
(25)
где 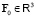 – значение F при
– значение F при 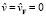 . Из (25) имеем
. Из (25) имеем
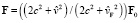 . (26)
. (26)
Искомая напряжённость 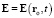 определяется следующими равенствами:
определяется следующими равенствами:
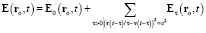 ; (27)
; (27)
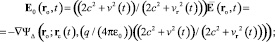 (28)
(28)
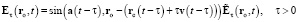 ; (29)
; (29)
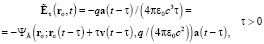 , (30)
, (30)
где 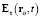 ,
, 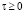 – напряжённость электрической силы в момент t в точке ro, обусловленная параметрами ЗМТ в момент t – τ;
– напряжённость электрической силы в момент t в точке ro, обусловленная параметрами ЗМТ в момент t – τ; 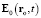 – напряжённость электродинамической силы в момент t в точке ro;
– напряжённость электродинамической силы в момент t в точке ro; 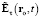 ,
, 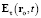 ,
, 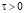 – напряжённость электроволновой силы возмущения, возникшего в момент t – τ и достигшего в момент t точки ro, без учёта и с учётом диаграммы направленности излучения.
– напряжённость электроволновой силы возмущения, возникшего в момент t – τ и достигшего в момент t точки ro, без учёта и с учётом диаграммы направленности излучения.
Равенство (27) – искомое гиперконтинуальное обобщение (13) на случай v(t) ≥ 0 подобно тому, как (16) – релятивистское обобщение (13) на случай v(t) < c. Формула (28) вытекает из (8), (26), выражает первый закон гиперконтинуальной электродинамики и является гиперконтинуальной альтернативой релятивистской формуле (15). Формулы (27), (29), (30) следуют из (9), (10), (13) применением классического правила сложения скоростей движения ЗМТ и распространения сферической волны и являются гиперконтинуальной альтернативой релятивистскому распространению области применимости этих формул на случай произвольной допустимой скорости v(t) < c. Формулы (19), (20) описывают излучение возмущения в виде сферической поперечной волны, центр которой движется со скоростью v(t – τ), а (27) – интерференцию электродинамической силы со всеми такими возмущениями (возникшими каждое в свой уникальный момент времени t – τ), которые достигают точки наблюдения ro в момент t. Формула (19) выражает свойство вакуума пропускать через себя только поперечные составляющие волн общего вида 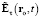 в виде поперечных волн
в виде поперечных волн 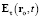 .
.
Функция 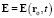 не является функцией какого-либо физического поля (одиночного или системы взаимодействующих полей), так как значения полевых функций такой системы (возможно, состоящей из одного поля) в данный момент времени в данной точке пространства зависят лишь от значений этих полевых функций и их производных в бесконечно близких к данным моментах времени и точках пространства (на этом основано использование математического аппарата дифференциальных уравнений для полевых функций). Электрическая сила не имеет материального носителя в виде физических полей-посредников при взаимодействии ЗМТ, рассматриваемых как механические системы с бесконечно большим числом степеней свободы, могущих обладать пространственной структурой, внутренним движением, импульсом, моментом импульса и кинетической энергией. Число степеней свободы системы ЗМТ всегда конечно и не может превышать утроенного числа ЗМТ. Некорректно говорить и о естественной геометрии электрической силы по аналогии с корректным понятием естественной геометрии физического поля.
не является функцией какого-либо физического поля (одиночного или системы взаимодействующих полей), так как значения полевых функций такой системы (возможно, состоящей из одного поля) в данный момент времени в данной точке пространства зависят лишь от значений этих полевых функций и их производных в бесконечно близких к данным моментах времени и точках пространства (на этом основано использование математического аппарата дифференциальных уравнений для полевых функций). Электрическая сила не имеет материального носителя в виде физических полей-посредников при взаимодействии ЗМТ, рассматриваемых как механические системы с бесконечно большим числом степеней свободы, могущих обладать пространственной структурой, внутренним движением, импульсом, моментом импульса и кинетической энергией. Число степеней свободы системы ЗМТ всегда конечно и не может превышать утроенного числа ЗМТ. Некорректно говорить и о естественной геометрии электрической силы по аналогии с корректным понятием естественной геометрии физического поля.
Замечательным свойством напряжённости (28) является то, что в отличие от (15) и подобно (8) она представима в виде 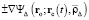 ,
, 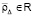 . Из (28) имеем
. Из (28) имеем
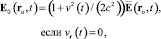 (31)
(31)
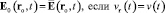 . (32)
. (32)
Величины (18), (32) равны, а (17), (31) совпадают до квадратичного члена ряда по скорости.
Согласно (17), (31), с ростом v(t) гиперконтинуальная напряжённость (28) растёт в направлении, нормальном v(t), подобно релятивистской (15), но лоренцево сокращение не имеет места. А согласно (18), (32), в направлении v(t) величина (28) так же не зависит от v(t), как и релятивистская (15). В итоге закон Гаусса не выполняется, и поток Φ(q, v) вектора 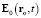 напряжённости электрической силы через любую замкнутую поверхность Ω, заключающую внутри себя ЗМТ, равен зависящей от скорости v = v(t) величине
напряжённости электрической силы через любую замкнутую поверхность Ω, заключающую внутри себя ЗМТ, равен зависящей от скорости v = v(t) величине
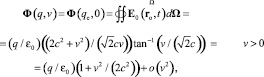 ; (33)
; (33)
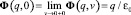 , (34)
, (34)
где 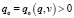 – эффективный заряд ЗМТ, в силу (33), (34) равный
– эффективный заряд ЗМТ, в силу (33), (34) равный
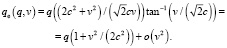 (35)
(35)
Такое нарушение закона Гаусса экспериментально подтверждено в опытах со сверхпроводниками и плазмой и объясняет наблюдения электрического импульса при космических ядерных испытаниях [12, 13]. Если в изначально электронейтральном проводнике начинает течь ток, то, согласно (33)–(35), он приобретает эффективный отрицательный заряд за счет приращения эффективного отрицательного заряда электронов вследствие их движения, что особенно заметно в сверхпроводниках. Плазма состоит из двух видов носителей заряда: относительно тяжёлые и потому относительно медленные положительно заряженные ионы, а также относительно лёгкие и потому относительно быстрые отрицательно заряженные электроны. При быстром разогреве плазмы электроны получают более высокое приращение скорости, чем ионы, что приводит, согласно (33)–(35), к более высокому приращению эффективного отрицательного заряда среднестатистического электрона по сравнению с приращением эффективного положительного заряда среднестатистического иона. В результате при сохранении равного количества ионов и электронов плазмы суммарный эффективный отрицательный заряд электронов превысит суммарный эффективный положительный заряд ионов. Избыточный, нескомпенсированный эффективный заряд совокупности электронов проявит себя в виде эффективного заряда всей плазмы.
Если 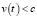 при всех
при всех 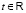 , то множество
, то множество
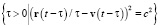
в (27) содержит единственное значение τ. Тогда
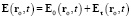 .
.
Если 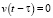 , то
, то
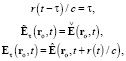
и (29), (30) принимают вид (9), (10). Замечательным свойством напряжённости (20) является возможность представления её модуля ньютоновым потенциалом (4) аналогично представлению (12) напряжённости (10):
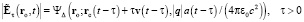 . (36)
. (36)
Но, в отличие от (12), представление (36) нельзя выразить волновым потенциалом (6). Это связано с тем, что в отличие от (10) напряжённость (20) при 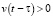 не удовлетворяет ни уравнению (11), ни какому-либо другому волновому уравнению.
не удовлетворяет ни уравнению (11), ни какому-либо другому волновому уравнению.
Вектор 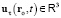 скорости возмущения
скорости возмущения 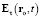 получается классическим сложением скорости
получается классическим сложением скорости 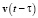 движения центра возмущения и скорости
движения центра возмущения и скорости 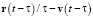 (модуль которой равен c) расширения сферического фронта волны:
(модуль которой равен c) расширения сферического фронта волны:
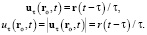 (37)
(37)
Частный случай (27) – случай
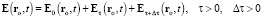 ,
,
при котором для каких-то значений 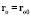 ,
, 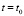 возможна ситуация, подобная которой невозможна в полевой и эфирной концепциях:
возможна ситуация, подобная которой невозможна в полевой и эфирной концепциях:
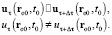
В релятивистской электродинамике волна (9) – математическая абстракция, для определения физического смысла которой волна (10) должна быть разложена в ряд Фурье по монохроматическим (синусоидальным) волнам с единой скоростью c. Каждая такая составляющая исходной волны (9) в виде монохроматической волны электрического поля соединена с однозначно определяемой ею синфазной с нею волной магнитного поля в единую монохроматическую электромагнитную волну, которая уже реальна. Интерференция всех таких монохроматических электромагнитных волн даёт электромагнитную волну общего вида (полихроматическую), физический смысл которой вторичен по отношению к фундаментальному, первичному физическому смыслу монохроматических волн. Но в гиперконтинуальной электродинамике магнитные волны, а вслед за ними монохроматические и полихроматические электромагнитные волны фиктивны [12, 13]. Чисто математическими абстракциями являются разложения волн (19), (20), (9), (10) в любые ряды. Реальный физический объект – сама исходная электрическая волна (19), (20), рассматриваемая соответственно с учётом и без учёта диаграммы направленности излучения, определяющей способность вакуума пропускать через себя волны. Электрическая волна переносит в пространстве потенциальную энергию электрического взаимодействия, не обладая импульсом, моментом импульса и кинетической энергией. Любая передача импульса и кинетической энергии между зарядами (в частности, давление света) дальнодействующая с учётом запаздывания.
Для волнового возмущения (19) со скоростью (37) вектор 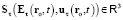 плотности потока потенциальной электрической энергии в точке ro в момент t получается произведением объёмной плотности энергии на вектор
плотности потока потенциальной электрической энергии в точке ro в момент t получается произведением объёмной плотности энергии на вектор 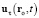 скорости возмущения:
скорости возмущения:
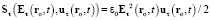 . (38)
. (38)
Интенсивность 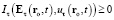 возмущения в точке ro в момент t в силу (38) равна
возмущения в точке ro в момент t в силу (38) равна
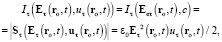 (39)
(39)
где 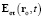 – эффективная напряжённость в точке ro в момент t, в силу (39) равная
– эффективная напряжённость в точке ro в момент t, в силу (39) равная
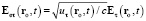 . (40)
. (40)
При 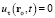 поток энергии в точке ro в момент t отсутствует, и из (40)
поток энергии в точке ro в момент t отсутствует, и из (40) 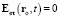 .
.
Пусть 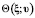 ,
, 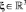 ,
, 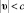 – временная задержка сигнала с приёмником в точке ξ и с источником в начале пространственных координат, движущимся со скоростью υ, причём скорость распространения сигнала получается классическим векторным сложением скорости υ со скоростью с модулем c распространения сигнала от неподвижного источника. Тогда
– временная задержка сигнала с приёмником в точке ξ и с источником в начале пространственных координат, движущимся со скоростью υ, причём скорость распространения сигнала получается классическим векторным сложением скорости υ со скоростью с модулем c распространения сигнала от неподвижного источника. Тогда
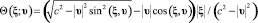 ; (41)
; (41)
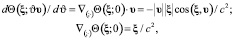 (42)
(42)
где 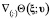 – результат применения градиента к функции (41) по второму аргументу.
– результат применения градиента к функции (41) по второму аргументу.
Из (8), (19), (20), (42) имеем равенство, раскрывающее физический механизм излучения:
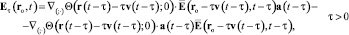 . (43)
. (43)
Из (43) видно, что электроволновая сила есть не что иное, как «оторвавшаяся» в момент 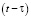 от ЗМТ электростатическая сила, распространяющаяся со скоростью
от ЗМТ электростатическая сила, распространяющаяся со скоростью 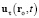 , которая получается классическим сложением скорости
, которая получается классическим сложением скорости 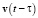 движения центра возмущения и скорости
движения центра возмущения и скорости 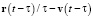 (её модуль равен c) расширения сферического фронта волны.
(её модуль равен c) расширения сферического фронта волны.
Итак, формулы (8), (27)–(30) или формулы (8), (27), (28), (43) определяют полную информацию об электрической силе, создаваемой в вакууме движущейся ЗМТ. Эти формулы удовлетворяют принципу относительности (все физические процессы протекают одинаково во всех ИСО вне зависимости от их неподвижности или равномерного и прямолинейного движения), так как содержат только относительную скорость v, а не какую-либо абсолютную скорость. Но вне полевой концепции принцип относительности не требует инвариантности волнового уравнения (11) относительно скорости v(t), и эта инвариантность не имеет места, так что напряжённость (20) удовлетворяет волновому уравнению (11) только при нулевой скорости, когда 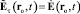 . Так как равенства (8), (27)–(30), (43) используют классическое правило сложения скоростей, то описываемая ими математическая модель электрической силы ЗМТ в вакууме инвариантна относительно преобразований Галилея.
. Так как равенства (8), (27)–(30), (43) используют классическое правило сложения скоростей, то описываемая ими математическая модель электрической силы ЗМТ в вакууме инвариантна относительно преобразований Галилея.
Заключение
Таким образом, удалось найти экспериментально подтверждённую альтернативу полевой концепции в виде концепции запаздывающего дальнодействия и реализовать последнюю в конкретную математическую модель. Разработанная в настоящей работе единая математическая модель электрической силы ЗМТ в вакууме и инертности её движения является альтернативой соответствующим релятивистским моделям. Она может служить основой для разработки всевозможных математических моделей систем зарядов в вакууме и материальных средах для конкретных областей новой, гиперконтинуальной, электродинамики.
Автор выражает глубокую благодарность Фёдору Фёдоровичу Менде (ФТИНТ им. Б.И. Веркина НАН Украины) за проведение в Харькове упомянутых в статье физических опытов, Анри Амвросьевичу Рухадзе (ИОФ им. А.М. Прохорова РАН, МФТИ) за организованное им и способствовавшее улучшению научных результатов статьи обсуждение гиперконтинуальной электродинамики и упомянутых харьковских опытов вообще и, в частности, на его всемирно знаменитом научном семинаре теоретического отдела ИОФ им. А.М. Прохорова РАН, а также другим участникам этого обсуждения, прежде всего Александру Михайловичу Игнатову (ИОФ им. А.М. Прохорова РАН), Вадиму Геннадьевичу Жотикову (МФТИ) и Александру Ивановичу Миланичу (МФТИ).

