Особый интерес представляет изучение потерь энергии при столкновении ионов с молекулярными мишенями. Такие процессы были рассмотрены теоретически в работах [1, 2] также с использованием приближения эйконала и метода сшивки, и было отмечено присутствие так называемого эффекта кратности столкновения. Суть этого эффекта заключается в значительном увеличении эффективного торможения иона в случае, когда ось молекулы параллельна направлению движения иона, по сравнению со случаем торможения на отдельных атомах молекулы. Данный эффект был рассчитан численно в [1, 2] с использованием приближения эйконала в виде, аналогичном приближению внезапных возмущений. Но ввиду ограничений на область применения этого метода расчёты торможения пришлось совмещать с методом сшивки. Путём комбинации двух расчётных методов авторам удалось получить достаточно простые аналитические формулы для расчёта эффективного торможения иона на двухатомной молекуле. Ими была рассчитана зависимость эффективного торможения от угла выстроенности оси молекулы. Но что для расчёта использовался метод сшивки, графики при малых и больших углах выстроенности получались разные и принципиально не стыковались друг с другом. Для их стыковки был предложен простой метод, заключающийся в введении функции, плавно переводящей один график в другой.
Целью данной работы было проверить достоверность результатов, полученных в [1] и [2] с использованием метода сшивки. В данной работе представлен расчёт эффективного торможения иона в рамках приближения эйконала, но без использования метода сшивки. В этом случае эффективное торможение можно сосчитать только численно.
Расчет торможения иона на молекуле
Рассмотрим рассеяние одноэлектронного иона с зарядом ядра Z на двухатомной молекуле с зарядовыми числами атомов Z1 и Z2. Положение иона относительно атомов задается векторами b1 и b2, а положение атомов относительно друг друга – вектором R. Угол выстроенности оси молекулы вдоль скорости иона v обозначен как θ. Таким образом для величин R, L и θ выполняется соотношение
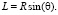(1)
Здесь мы будем рассчитывать только ту часть торможения, которая связана с переходами в оболочках иона – κр. Исследование именно этой части торможения наиболее интересно при кратных столкновениях.
Получим выражение для эффективного торможения. Подобный расчет был получен в работе [1]. В частности, было показано, что эффективное торможение иона может быть представлено в следующем виде:
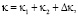(2)
где κj имеет смысл эффективного торможения иона на отдельном j-м атоме молекулы (j = 1,2), а Δκ – поправка, учитывающая интерференционный вклад кратных последовательных столкновений иона с атомами молекулы. Ранее было установлено что поправка Δκ зависит от угла θ выстроенности молекулы.
Эффективное торможение иона при столкновении с молекулой можно расчитать по формуле из 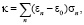[3]
(3)
где εn и ε0 – энергии возбужденного и основного состояний электрона снаряда, σn – сечение соответствующего неупругого перехода. Как и ранее, согласно приближению эйконала, сечение σn может быть записано в виде
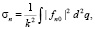(4)
где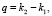 
k1 и k2 – импульсы до и после рассеяния 
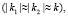интегрирование по q в (4) ведется от 
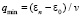до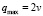 
, v – скорость иона, 
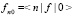– амплитуда неупругого рассеяния иона на молекуле,
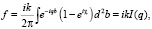(5)
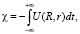(6)
где b – параметр удара иона относительно центра масс молекулы, U(R, r) – энергия взаимодействия иона с молекулой. Следуя [1] и [2] представим U в виде суммы U1 и U2, где Uj – энергия взаимодействия иона с j-й атомом молекулы (рассчитывалась в рамках модели Дирака – Хартри – Фока – Слейтера (ДХФС) [4]). С учетом сказанного, эйкональная фаза (6) примет вид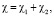 
где
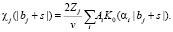(7)
Здесь Zj – заряд ядра j-го атома молекулы, Ai и αi – коэффициенты модели ДХФС для j-го атома молекулы, K0 – функция Макдональда, bj – параметр удара иона относительно j-го атома молекулы, s – проекция координаты r электрона иона на плоскость параметра удара. Учитывая, что
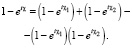(8)
Амплитуда (5) может быть представлена в виде
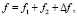(9)
где fj – амплитуда рассеяния иона на j-м атоме молекулы
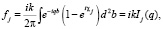(10)
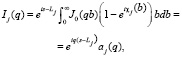(11)
где Lj – проекция радиус-вектора j-го атома относительно центра масс молекулы на плоскость параметра удара, а
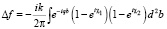(12)
– интерференционная поправка к амплитуде, учитывающая вклад обоих атомов молекулы. В результате эффективное торможение (3) иона при столкновении с двухатомной молекулой с учётом (12) может быть записано в аналогичной форме
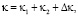(13)
где κj – имеет смысл эффективного торможения иона на отдельном j-м атоме молекулы, а Δκ – поправка, учитывающая интерференционный вклад кратных последовательных столкновений иона с атомами молекулы. Величины κ и κj рассчитываются по формулам
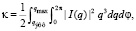(14)
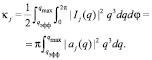(15)
Здесь интегрирование по q ведётся в интервале от qэфф до qmax, где qэфф – эффективное значение минимального передаваемого импульса, аналогичное эффективному заряду из работы [5]. Согласно формулам (13)–(15), величины κ и Δκ будут зависеть от ориентации оси молекулы относительно направления скорости иона, т.е. от угла выстроенности θ.
Для исследования зависимости Δκ(θ) удобно ввести относительное торможение
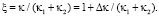(16)
Проанализировав формулы, можно вывести более простую формулу для расчета поправки Δκ. Учитывая (13)–(15), имеем
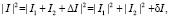(17)
где
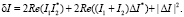(18)
Анализ формулы (18) показывает, что основной вклад в δI дает первое слагаемое, поэтому приближенно можно считать, что
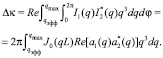(19)
В случае одинаковых атомов в молекуле (Z1 = Z2) формула (19) упрощается к виду
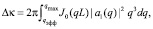(20)
а суммарное эффективное торможение (13) на молекуле равно
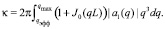(21)
Из формулы (21) явно видно, что в этом приближении при малых θ(L > 0) торможение на всей молекуле κ будет ровно в 2 раза больше суммарного торможения 2κ1 на двух отдельных атомах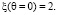 
Торможение на многоатомных молекулах
Наиболее актуальными в настоящее время являются процессы торможения и потерь энергии на многоатомных системах, в том числе и таком объекте, как нанотрубки.
Рассмотрим торможение водородоподобного иона на линейной многоатомной молекуле. Будем искать амплитуду рассеяния в виде
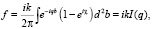(22)
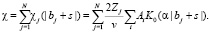(23)
1. Если N = 2
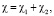
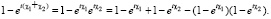(24)
Пусть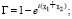 
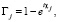тогда
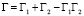. (25)
2. Если N = 3
То есть
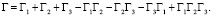(26)
3. В общем случае
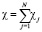, (27)
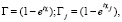(28)
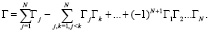(29)
так как
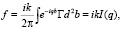(30)
то
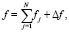(31)
где
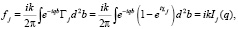(32)
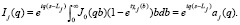(33)
Вернемся к торможению
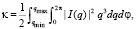(34)
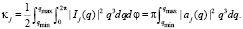(35)
Тогда
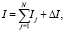где 
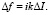(36)
Тогда
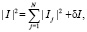(37)
где
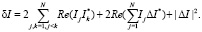(38)
Основной вклад в δI даёт первое слагаемое, т.е.
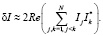(39)
С учетом этого, например, для N = 3 имеем
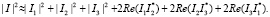(40)
В результате
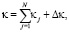(41)
где
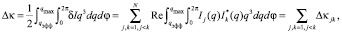(42)
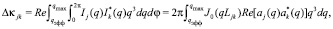(43)
где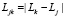 
– расстояние между j-м и k-м ядрами молекулы в проекции на плоскость параметра удара. В данном случае –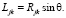 
Так, при N = 3, имеем
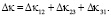(44)
Пусть молекула состоит из одинаковых атомов, находящихся на одинаковом расстоянии друг от друга (цепочка атомов). Параметры цепочки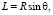 
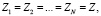
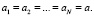
В этом случае
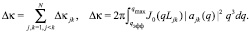(45)
Для расчета Δκ нужно перебрать все пары атомов в «молекуле».
1. Смотрим пары атомов, находящихся друг от друга на расстоянии L. Их (N – 1) пар. Их общий вклад в поправку Δκ будет равен
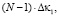где 
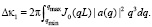(46)
2. Смотрим пары на расстоянии 2L. Их (N – 2) пара. Их общий вклад в Δκ равен
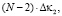где 
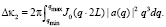(47)
3. Смотрим пары на расстоянии n•L. Их (N – n) пара. Их общий вклад в Δκ равен
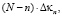где 
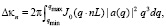(48)
где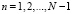 
.
Тогда
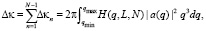(49)
где
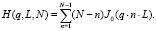(50)
Эффективный переданный импульс qэфф находим в общем случае
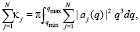(51)
где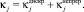 
Поправку на ориентационный эффект рассчитаем по прежней формуле
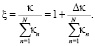(52)
Результаты расчетов торможения на многоатомных молекулах
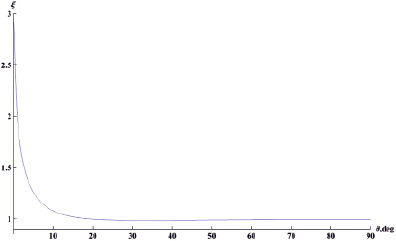
Рис. 1. Зависимость относительного эффективного торможения иона Li+2 на молекуле CO2 от угла выстроенности при 150 МэВ/нукл
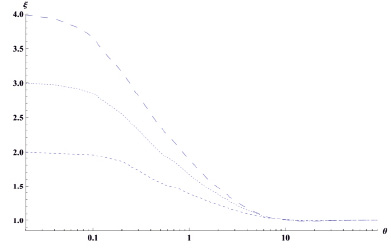
Рис. 2. Зависимость относительного эффективного торможения иона He+ на цепочке из атомов C от угла выстроенности при 150 МэВ/нукл. Крупный пунктир – цепочка из 4 атомов углерода, средний пунктир – цепочка из 2-х атомов углерода, а мелкий пунктир – цепочка из 3-х атомов C
Как видно из графика на рис. 2, при угле выстроенности θ = 0 торможение на цепочке из N-атомов в N раз больше суммарного торможения на отдельных атомах, т.е. в N2 раз больше торможения на одном атоме. В нашем случае N = 2, 3, 4. Также из рис. 2 видно, что характер зависимости ξ(θ) в сравнении с предыдущими расчётами в целом остался таким же – при уменьшении угла θ величина ξ(θ) стремится к своему максимальному значению. Однако стоит отметить, что согласно нашим расчётам переход к значению теперь происходит при другом значении угла θ в отличие от значения, полученного ранее в работе [1] в рамках метода сшивки.
Выводы
В работе на основе приближения эйконала развит общий метод расчёта эффективного торможения быстрых ионов на многоатомных молекулах. В рамках данного метода была исследована зависимость эффективного торможения водородоподобного иона на молекуле от энергии налетающей частицы.
Рассмотрены потери энергии быстрых водородоподобных ионов при столкновениях с молекулами (в том числе многоатомными). Исследована зависимость эффективного торможения иона на молекуле от угла выстроенности её оси относительно скорости иона. Получено, что учёт кратности столкновений приводит к увеличению эффективного торможения иона в случае, когда ось молекулы параллельна направлению движения иона. Кратность же увеличения торможения зависит от числа атомов в молекуле.