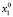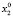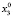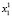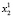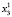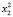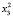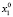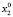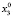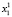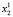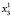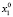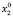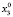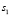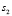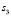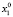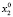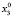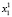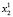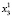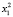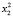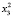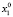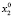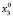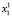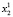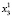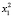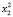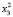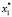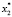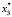Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Спектр приложений двоичных динамических моделей необычайно широк и с каждым годом количество объектов и задач, где требуется их использование, только возрастает. Классическим примером является двоичный синхронный автомат, являющийся моделью многих дискретных устройств в системах управления, вычислительной технике, телемеханике. К современным приложениям двоичных динамических моделей относятся задачи биоинформатики, экономики, социологии и ряда других, казалось бы далеких от применения двузначных переменных, областей. В связи с этим в существенной степени повышается актуальность разработки новых и совершенствование существующих методов качественного анализа поведения траекторий двоичных динамических систем (ДДС).

Как известно, целью качественного анализа динамической системы (не только двоичной) является получение положительного или отрицательного ответа на вопрос: Выполняется ли в заданной системе требуемое динамическое свойство? Перефразируем этот вопрос следующим образом: Удовлетворяет ли поведение траекторий динамической системы некоторой совокупности ограничений, характеризующих свойство? Далее будем использовать именно эту трактовку цели качественного анализа динамических свойств системы.

Для ДДС, функционирование которых рассматривается на конечном интервале времени, такие ограничения являются булевыми и записываются на языке булевых уравнений или булевых формул с кванторами. Первый тип ограничений приводит к необходимости решения SAT-задачи (задачи булевой выполнимости [1]); второй тип ограничений связан с решением задачи TQBF (проверки истинности квантифицированных булевых формул [2]). Первая задача является типичным представителем класса сложности NP, а вторая задача – класса сложности PSPACE. Как известно, PSPACE-полнота дискретной задачи дает более сильное свидетельство о ее труднорешаемости, чем NP-полнота. В силу этого сведение задачи качественного анализа ДДС к SAT-задаче более предпочтительно, чем сведение к задаче TQBF. В общем случае исследование не каждого свойства ДДС можно представить на языке булевых уравнений.

Теоретическая возможность использования булевых ограничений (а именно, булевых уравнений) в качественном анализе ДДС впервые была продемонстрирована в работе [3]. Следует, однако, отметить, что применение этого подхода на практике в то время сдерживалось отсутствием эффективных алгоритмов и программ решения булевых уравнений (особенно с большим числом неизвестных переменных), позволяющих в существенной степени сократить пространство поиска. В последнее десятилетие в результате интенсивных исследований в этой области появилось достаточное количество разнообразных эффективных решателей булевых уравнений (SAT-решателей), использующих современные достижения (новые эвристики, быстрые структуры данных, параллельные вычисления и др.) в решении задачи булевой выполнимости. Аналогичные процессы (но с некоторым запаздыванием) наблюдаются и в области создания все более эффективных алгоритмов и программ решения задачи TQBF. Таким образом, к настоящему времени имеются все необходимые предпосылки систематического развития метода булевых ограничений в качественном анализе ДДС, его программной реализации и применении в решении научных и прикладных задач.

Кроме метода булевых ограничений, к ДДС применимы и другие методы качественного анализа, к которым относятся дедуктивный анализ, model checking и метод редукции. Каждый из этих методов (включая и метод булевых ограничений) имеет свои ограничения, преимущества и недостатки. Общим недостатком является то, что все методы носят переборный характер и проблема сокращения перебора является фундаментальной для этих методов.

Важность дедуктивного анализа [4], подразумевающего применение аксиом и правил вывода для доказательства правильности функционирования системы, признается широким кругом специалистов, но это трудоемкий и поэтому редко применяемый метод. В методе model checking [5] в качестве языка спецификации требуемого свойства используется язык темпоральных логик, который непривычен для специалистов по автоматной динамике. Метод редукции [6] связан с построением упрощенной (в определенном смысле) модели исходной системы, исследовании ее свойств и условий переносимости этих свойств в исходную сложную систему. Условия переносимости свойств носят при этом только достаточный характер. Простота идеи метода редукции в качественном анализе ДДС сталкивается с проблемой выбора упрощенной системы, удовлетворяющей всем условиям метода.

Практическое использование метода булевых ограничений предполагает алгоритмизацию и автоматизацию следующих процессов:

1) разработка ориентированного на специалиста по динамике систем логического языка спецификации динамических свойств;

2) построение модели динамического свойства в виде булевого ограничения того или иного типа, удовлетворяющей логической спецификации свойства и уравнениям динамики двоичной системы;

3) представление полученной модели в международном формате DIMACS [7] или QDIMACS [8];

4) выбор (разработка) эффективного параллельного (распределенного) решателя задачи выполнимости булевых ограничений (SAT или TQBF решателя);

5) разработка инструментальных средств создания программных сервисов;

6) разработка сервисов для качественного исследования разнообразных динамических свойств ДДС.

Целью настоящего исследования является решение только первых двух задач применительно к алгоритмизации качественных исследований автономных (без управляющих входов) синхронных ДДС. Такие системы в англоязычных публикациях принято называть синхронными булевыми сетями (Boolean network). Другие аспекты применения метода булевых ограничений (в том числе и для ДДС с управляющими входами) являются предметом следующих публикаций.

Математическая модель автономной ДДС

Пусть X = Bn (B = {0, 1} – множество двоичных векторов размерности n (пространство состояний ДДС). Через t∈T = {1,…,k} обозначим дискретное время (номер такта).

Для каждого состояния x0∈X, называемого начальным состоянием, определим траекторию x(t, x0) как конечную последовательность состояний x0, x1,…, xk из множества X. Далее будем рассматривать ДДС, в которых каждая пара смежных состояний xt, x(t – 1) (t∈T) траектории связана отношением

xt = F(xt – 1). (1)

Здесь F:X>X – векторная функция алгебры логики, называемая функцией переходов. Таким образом, для любых x0∈X система булевых уравнений (1) представляет модель динамики поведения траекторий ДДС в пространстве состояний X на конечном интервале времени T = {1, 2,…,k}. Здесь и далее величина k в определении множества T предполагается наперед заданной постоянной. Такое ограничение является вполне естественным. Дело в том, что при качественном анализе поведения траекторий ДДС практический интерес представляет вопрос о том, что можно сказать о выполнимости какого-либо динамического свойства при фиксированном, не слишком большом k. Выбор величины k в каждом конкретном случае осуществляется исходя из априорных сведений о длительности протекания процессов в моделируемой дискретной системе.

Известно [3], что система булевых уравнений (1) с начальным состоянием x0∈X для T = {1, 2,…,k} эквивалентна одному булевому уравнению вида

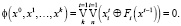(2)

При k = 1 (рассматриваются только одношаговые переходы) уравнение (2) приобретает вид

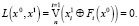(3)

Решения этого уравнения определяют направленный граф, состоящий из 2n вершин, отмеченных одним из 2n состояний множества X. Вершины x0 и x1 графа соединены дугой, направленной от состояния x0 к состоянию x1. Такой граф в теории двоичных автоматов называется диаграммой переходов. Представление поведения ДДС в виде диаграммы переходов весьма наглядно как при построении траекторий, так и исследовании их свойств, но практически реализуемо лишь для небольших размерностей n вектора состояния x∈X.

Языковые средства спецификации динамических свойств

Наиболее удобно задавать спецификацию динамического свойства на языке формальной логики. Следуя работе [6], обозначим через X0∈X, X1∈X, X*∈X – множества начальных, допустимых и целевых состояний.

Основными синтаксическими элементами логической формулы динамического свойства являются: 1) предметные переменные (компоненты векторов x0, x1,…, xk, время t); 2) ограниченные кванторы существования и всеобщности; 3) логические связки v, &; заключительные формулы. Заключительная формула представляет утверждение о принадлежности некоторых состояний множества траекторий x(t, x0) (x0∈X0) оценочным множествам X* и X1.

Следует отметить, что использование ограниченных кванторов существования и всеобщности обеспечивает привычный для специалиста по динамике вид записи динамического свойства. В процессе построения булевой модели свойства для системы (1) ограниченные кванторы заменяются на обычные согласно следующим определениям:

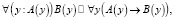
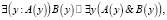
где A(y) – предикат, ограничивающий значение переменной y.

В силу конечности области изменения переменной t, ограниченные кванторы существования и всеобщности по этой переменной заменяются на равносильные формулы, не содержащие кванторов

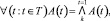
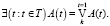
В дальнейшем будем предполагать, что элементы множеств X0, X1, X* определяются соответственно нулями следующих булевых уравнений

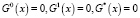
или характеристическими функциями этих множеств , .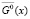

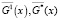С учетом ограничения на начальные состояния G0(x) = 0 наряду с уравнениями (2, 3) для сокращения записи будем использовать следующие булевы уравнения:

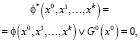(4)

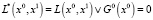. (5)

Предварительный качественный анализ автономных ДДС

На этапе предварительного анализа может быть выявлено (при необходимости) ветвление состояния (множество его непосредственных предшественников), наличие равновесных состояний и замкнутых траекторий (циклов).

Состояние x1 в (3) будем называть последователем состояния x0, а x0 – предшественником состояния x1. В автономной ДДС каждое состояние имеет только одного последователя, а число предшественников данного состояния может изменяться от нуля до 2n – 1. Все непосредственные предшественники x0 состояния s∈X являются нулями булева уравнения

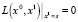. (6)

Если уравнение (6) не имеет решений, то предшественники состояния s отсутствуют.

Равновесные состояния (если они существуют) являются решениями булева уравнения

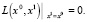
Траектория x0, x1,…, xk называется циклом длины k, если состояния x0, x1,…, xk-1 попарно отличны друг от друга и xk = x0. Циклическая последовательность длины k (если она существует) является решением булева уравнения

,

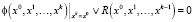где 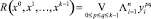= 0 (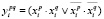) – условия попарного различия множества состояний C цикла длины k. Если ни одно из состояний цикла не имеет предшественников, не принадлежащих множеству C, то такой цикл называется изолированным. Пусть элементы s множества C определяются решением булева уравнения Gc(s) = 0. Тогда несложно показать, что условие изолированности цикла эквивалентно отсутствию нулей у следующего булева уравнения:

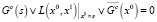. (7)

Решения уравнения (7) (если они существуют) определяют состояния цикла, имеющие предшественников, не принадлежащих множеству C.

Так как равновесное состояние является циклом длины k = 1, то условие его изолированности аналогично условию изолированности с k ≥ 2 за тем отличием, что Gc(s) имеет вид полной дизъюнкции, определяющей это равновесное состояние.

Неизолированные равновесные состояния и циклы в дальнейшем будем называть аттракторами.

Спецификация динамических свойств типа достижимости

Основным свойством ДДС, необходимость в проверке которого наиболее часто возникает на практике, является традиционно изучаемое в теории графов (в нашем случае таким графом является диаграмма переходов) свойство достижимости и его различные вариации. В [9] достижимость определяется как классическая задача анализа поведения траекторий ДДС.

Определение этого свойства связано с заданием введенных ранее множеств X0, X*, X1 (соответствующих этим множествам булевых уравнений). Предполагается, что для множеств X0, X*, X1 выполняется ограничение

.

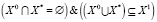В силу конечности множества T свойство достижимости и его вариации далее будем понимать как свойство практической достижимости (достижимости за конечное число тактов). Рассматриваются следующие свойства типа достижимости:

1. Основное свойство достижимости множества X* из множества X0 формулируется следующим образом: любая траектория, выпущенная из множества начальных состояний X0, достигает целевого множества X*. С использованием ограниченных кванторов существования и всеобщности, формула этого свойства имеет вид:

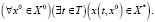
2. Свойство безопасности обеспечивает для любой траектории, выпущенной из X0, недостижимость множества X*:

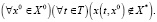
3. Свойство одновременной достижимости. В ряде случаев может выставляться более «жесткое требование», которое состоит в том, чтобы каждая траектория достигала целевого множества ровно за k тактов (k∈T):

.

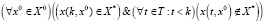4. Свойство достижимости при фазовых ограничениях:

.

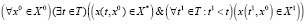Это свойство гарантирует, что все траектории, выпускаемые из множества X0, до момента попадания в целевое множество X* находятся в множестве X1.

5. Свойство притяжения. Пусть X* является аттрактором. Тогда логическая формула свойства притяжения совпадает с формулой основного свойства достижимости:

,

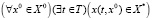т.е. для каждой траектории, выпущенной из множества X0, существует момент времени t∈T, начиная с которого траектория не выходит за пределы множества X*. Множество X0 в этом случае принадлежит части области притяжения множества X*(X0∈Xa, где Xа – полная область притяжения (бассейн) аттрактора).

Отметим, что все переменные в приведенных формулах свойств являются фактически связанными, так как траектория x0, x1,…, xk полностью определяется начальным состоянием. Так как кванторы по переменной t заменяются на операции многоместной дизъюнкции или конъюнкции соответствующих предикатов, в каждой из формул остается единственный ограниченный квантор всеобщности (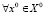), что позволяет записать условия выполнимости этих свойств на языке булевых уравнений (в виде SAT-задачи).

Приведем два свойства, проверка которых приводит к необходимости решения задачи TQBF.

6. Свойство связности целевого множества:

,

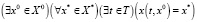т.е. существует начальное состояние x0∈X0 такое, что каждое целевое состояние x*⊆X* в некоторый момент t∈T достижимо, что означает существование соответствующей этому состоянию траектории, такой, что все целевые состояния x*∈X* принадлежат данной траектории.

7. Свойство тотальной достижимости множества X* из X0:

,

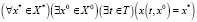т.е. каждое целевое состояние является достижимым из X0.

Проверка выполнимости динамических свойств

Для свойств (1–5) проверка их выполнимости сводится к поиску нулей булева уравнения, технология формирования которого носит стандартизованный характер и подробно рассматривается только для основного свойства достижимости. Свойства (6, 7) приводят к задаче проверки истинности квантифицированной булевой формулы.

1. Основное свойство достижимости. Его логическая формула имеет вид

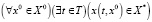. (8)

С учетом (4) запишем формулу (8) в виде

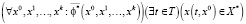, (9)

где 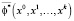– характеристическая функция множества состояний траектории, выпущенной из начального состояния x0∈X0. Избавимся от квантора существования в (9). Тогда будем иметь

,

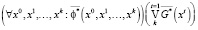где 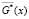– характеристическая функция множества X*. Заменим ограниченные кванторы всеобщности на обычные кванторы. В результате получим

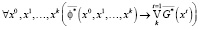. (10)

Формула (10) истинна тогда и только тогда, когда тождественно истинно подкванторное выражение, т.е.

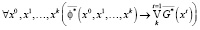. (11)

Тождественная истинность импликации означает, что булева функция 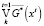является логическим следствием функции 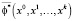, т.е. любая траектория с начальным состоянием x0∈X0 достигает целевого множества X*.

Выполнимость тождества (11) эквивалентна отсутствию нулей у булева уравнения

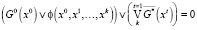. (12)

При получении (12) мы избавились от импликации и заменили ϕ*(x0, x1,..., xk) на 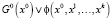. Если уравнение (12) имеет хотя бы одно решение, то свойство достижимости не имеет места. Такое решение представляет (в определенном смысле) контрпример для проверяемого свойства и может помочь исследователю выявить причину возникновения ошибки.

Далее для краткости изложения для каждого свойства (2–4) выпишем только уравнение типа (12), предлагая читателю самостоятельно воспроизвести необходимые рассуждения, близкие к тем, которые даны для основного свойства достижимости.

2. Свойство безопасности

.

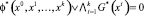3. Свойство одновременной достижимости

.

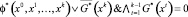4. Свойство достижимости при фазовых ограничениях

.

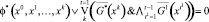5. Свойство притяжения. Выполнимость этого свойства проверяется в два этапа. На первом этапе выясняется, является ли множество X* аттрактором. Если ответ положительный, то на втором этапе проверяется основное свойство достижимости. Если X* достижимо из X0, то все условия свойства притяжения выполнены.

6. Свойство связности

.

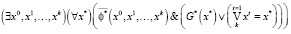7. Свойство тотальной достижимости`

.

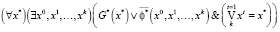Для свойств (6, 7) скалярная форма равенства двух булевых векторов xt = x* имеет вид

.

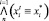Пример

Продемонстрируем изложенную выше технологию качественного анализа автономных ДДС с использованием метода булевых ограничений при проверке выполнимости некоторых из перечисленных выше свойств для модели 3.2 из работы [10]:

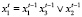
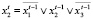(13)

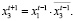
Обозначим через x0∈X = B3 начальное состояние модели (13). Пусть T = {1, 2}. Выпишем требуемые для спецификации свойств функции одношагового и двухшагового переходов модели (13):

;

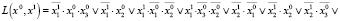
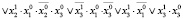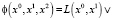(14)

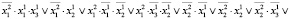
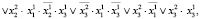
где знаком «•» обозначена операция конъюнкции.

Для проверки выполнимости каждого свойства задаются начальное (X0) и целевое (X*) множества, определяемые нулями уравнений G0(x) = 0, G*(x) = 0 или характеристическими функциями этих множеств (см. п. 2). В качестве SAT-решателя используется решатель инструментального комплекса (ИК) РЕБУС [11], а TQBF-решателя – DepQBF [12]. Кодировка переменных в булевых моделях рассматриваемых ниже свойств для этих решателей приведена в табл. 1, булевы модели этих свойств в форматах DIMACS и QDIMACS расположены в табл. 2.

Таблица 1

Кодировка переменных

Таблица 2

Булевы модели свойств

1. Основное свойство достижимости (k = 2). Пусть X0 = {x∈X: x1 = 0}, X*={x∈X: x1 = 1}. Начальное и целевое множества определяются соответственно уравнениями G0(x) = x1 = 0 и 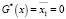. Булево уравнение (12) в этом случае приобретает вид

,

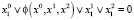где функция ϕ(x0, x1, x2) определена в (14). Решатель ИК РЕБУС выдает ответ «unsat» (уравнение не имеет нулей), таким образом свойство достижимости X* из X0 выполняется, что наглядно видно из следующей диаграммы переходов, приведенной на рисунке.

2. Циклы длины k = 2. Циклическая последовательность длины 2 (если она существует) является решением булева уравнения

.

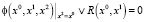Функция 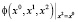имеет вид

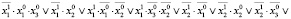
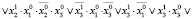
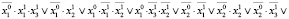
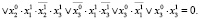
Выражение R(x0, x1) при нахождении цикла не включалось в уравнение, так как циклы длины k = 1 (равновесные состояния) в модели (13) отсутствуют. С помощью решателя ИК РЕБУС получены два ответа (в выходном формате DIMACS): 1 2 3 4 5 -6 0 и 1 2 -3 4 5 6 0, соответствующие циклическим последовательностям (рисунок): {(1 1 1), (1 1 0)} и {(1 1 0), (1 1 1)}. Множества состояний обоих циклов совпадают, что означает наличие в модели (13) одного цикла длины k = 2.

Диаграмма переходов системы (13)

3. Свойство изолированности цикла. Если элементы s множества состояний C цикла длины k = 2 определяются решением булева уравнения Gc(s) = 0, то условие изолированности цикла эквивалентно отсутствию нулей у следующего булева уравнения:

.

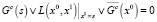Так как C = {(1 1 1), (1 1 0)}, имеем

, ,

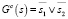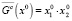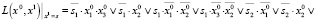
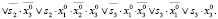
Для этого уравнения решатель ИК РЕБУС находит два решения: -1 2 3 4 5 -6 0 и -1 2 -3 4 5 -6 0 (в двоичном представлении согласно кодировке переменных в табл. 1 это пары состояний (0 1 1), (1 1 0) и {(0 1 0), (1 1 0)). Таким образом, состояние цикла (1 1 0) имеет два предшественника, (0 1 1) и (0 1 0), не принадлежащих множеству состояний цикла. Это означает, что свойство изолированности цикла не выполняется, т.е. данный цикл является аттрактором.

4. Свойство притяжения. Пусть X* = C является аттрактором. Логическая формула свойства притяжения совпадает с формулой основного свойства достижимости

,

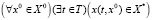а соответствующее булево уравнение для нашего случая имеет вид

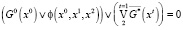. (15)

Выпишем функции G0(x0), ϕ(x0, x1, x2) и 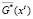. Функция ϕ(x0, x1, x2) приведена в (14). Для X* = C выражение 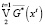равно 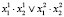. Рассмотрим два варианта задания множества начальных состояний X0, для случаев выполнения (А) и невыполнения (B) свойства притяжения за k = 2 тактов.

A. Пусть 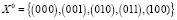. Тогда

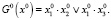
В этом случае для булевого уравнения (15) выдается ответ «unsat». Свойство притяжения для заданного множества X0 выполняется.

B. Пусть 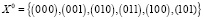. Тогда

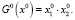
В этом случае ИК РЕБУС для уравнения (15) находит решение: 1 -2 3 4 -5 -6 -7 8 9 0, которое соответствует траектории {(1 0 1),(1 0 0),(0 1 1)}. Эта траектория с начальным состоянием x0 = (1 0 1) за два такта не достигает множества X* = C, что означает невыполнимость свойства притяжения для заданного X0.

5. Свойство связности. Логическая формула свойства связности имеет вид следующего высказывания:

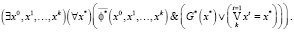(16)

Для k = 2 ϕ*(x0, x1, x2) = G0(x0)∨ϕ(x0, x1, x2), где функция ϕ(x0, x1, x2) приведена в (14). В качестве начального выберем состояние (1 0 1). Тогда 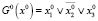. Пусть целевое множество X* = {(0 1 1), (1 0 0)}. В этом случае функция G*(x*) имеет вид

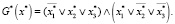
Запишем G*(x*) в формате КНФ:

(

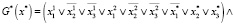
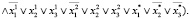
Используя закон Де-Моргана, найдем отрицание функции ϕ*(x0, x1, x2). Подставив в (16) все полученные функции и с учетом кодировки булевых переменных (табл. 1), получим булеву модель в формате QDIMACS (табл. 2). Решатель DepQBF выдает ответ «sat», что означает истинность высказывания (16). Свойство связности для заданных X0, X*, T = {1, 2} выполнено.

Заключение

К основным достоинствам метода булевых ограничений в качественном исследовании ДДС относятся:

1. Привычный для специалиста по автоматной динамике логический язык спецификации динамического свойства за счет использования ограниченных кванторов существования и всеобщности.

2. По формуле свойства и уравнениям динамики автоматически выполняется построение соответствующего булева уравнения или квантифицированной булевой формулы.

3. Достаточно просто автоматизируется процесс преобразования получаемых булевых выражений в конъюнктивную нормальную форму с дальнейшей генерацией файла в форматах DIMAX и QDIMAX, являющихся входными для SAT-решателей и QBF-решателей.

4. Проблема сокращения перебора в той или иной мере решается разработчиками этих решателей и экранирована от специалистов по качественному анализу ДДС.

5. Обеспечивается возможность решения задачи качественного анализа ДДС для больших размерностей вектора состояния n на достаточно продолжительном промежутке времени T. По числу состояний метод булевых ограничений количественно соизмерим с методом model checking. В силу того, что в последние годы наблюдается существенный рост производительности специализированных алгоритмов решения SAT и TQBF-задач, общее количество переменных в булевой модели свойства для современных решателей может измеряться тысячами.

Программное обеспечение процесса качественного анализа ДДС на основе метода булевых ограничений реализуется в рамках сервис-ориентированного подхода [13] с использованием специализированных решателей булевых уравнений [11, 14]. В работе [15] приведен пример реализации метода булевых ограничений на основе сервис-ориентированного подхода для поиска циклов и равновесных состояний в генных регуляторных сетях.

Следует отметить, что метод булевых ограничений является достаточно общим методом качественного анализа ДДС на конечном интервале времени. Он применим не только к автономным системам, но и к системам с управляющими входами, к системам с глубиной памяти больше единицы, к ДДС общего вида, когда функция переходов неразрешима относительно состояния xt и имеет вид F(xt, xt-1) = 0. Для ДДС со входами особое значение приобретает свойство управляемости и его различные вариации. Кроме задач анализа ДДС метод булевых ограничений применим к задачам синтеза обратной связи (статической или динамической, по состоянию или по входу), обеспечивающих в синтезируемой системе выполнение требуемого динамического свойства.

Исследование выполнено при поддержке РФФИ, проект № 18-07-00596/18.