Памяти моего учителя, профессора Г.М. Бакана посвящается
Одна из важнейших задач теории управления состоит в эффективном построении областей достижимости или их аппроксимаций для изучаемых динамических систем. Для линейных систем, как показано в [1], хорошо разработана техника эллипсоидального оценивания областей достижимости сверху и снизу. Где рассматривается задача оценивания множеств достижимости управляемых динамических систем, описываемых дифференциальными уравнениями с импульсным управлением и неполной информацией о начальных данных.
Работа [2] посвящена решению задачи масштабируемости эллипсоидального метода оценивания множеств достижимости линейных систем. Задача решается с помощью эллипсоидального метода оценивания множества достижимости, а именно, построением внешних оценок.
Особенности задач управления неустойчивыми объектами рассматриваются многими как отечественными, так и зарубежными авторами. Основной особенностью ограниченного управления неустойчивым объектом является ограниченность области притяжения (асимптотической устойчивости) стабилизируемого состояния в фазовом пространстве системы. Нахождение границ области устойчивости стабилизируемого состояния для нелинейных систем в общем случае является сложной задачей. Преодоление указанной трудности состоит в нахождении оценки области устойчивости в виде эллипсоида и условий достижения его максимальных размеров [3].
Решение данных задач заключается в обеспечении сходимости используемых алгоритмов оценивания параметров с помощью эллипсоидов.
Так в работе [4] рассматривалась сходимость алгоритмов оценивания с помощью эллипсоидов в задаче оценивания параметров линейной регрессии, при линейных ограничениях на вектор входных переменных. Там, в частности, было показано, что сходимость можно обеспечить за счет преднамеренного искажения входных сигналов.
В статье [5] рассмотрена задача параметрического оценивания для линейных многомерных систем с интервальной неопределенностью в данных. Где для нахождения интервальных оценок невыпуклых информационных множеств системы использован алгоритм, основанный на вычислении интервальных решений для интервальных систем линейных алгебраических уравнений с квадратной матрицей.
В данной работе рассматриваются вопросы сходимости алгоритмов эллипсоидального оценивания в условиях, когда на входные функции в уравнении регрессии накладываются ограничения.
Рассмотрим уравнение линейной регрессии
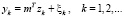(1)
где число yk и вектор zk значений входных функций (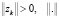
– евклидова норма вектора) предполагаются известными в каждый момент k дискретного времени, 
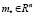– вектор неизвестных (оцениваемых) параметров (Rn – n-мерное евклидово вещественное пространство), Т – символ транспонирования. Неизвестная величина (помеха) ξk предполагается ограниченной
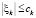, (2)
где ck ≥ 0 – известное число. Вектор zk ограничен.
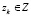, (3)
где Z – выпуклое компактное множество в Rn.
Априорно задано, что вектор m* принадлежит некоторому ограниченному множеству E0. Без ограничения общности будем полагать, что это множество является эллипсоидом
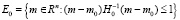, (4)
где вектор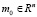 
(априорная оценка вектора m*) и симметрическая матрица 
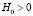считаются известными.
Приведенных здесь исходных данных достаточно для построения так называемых эллипсоидальных оценок Eк вектора параметров m*. Эти оценки имеют вид многомерных эллипсоидов
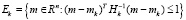, (5)
таких, что
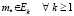. (6)
При этом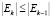 
, где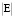 
– многомерный объем эллипсоида Е.
В (5) –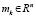 
– центр симметрии эллипсоида, Hk – положительно определенная 
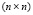– матрица. Эти определяющие оценку Ek величины вычисляются рекуррентно в соответствии с тем или иным алгоритмом эллипсоидального оценивания [6, 7].
Рассмотрим класс или множество подобных алгоритмов, определяемых соотношениями
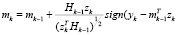, (7)
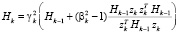, (8)
где начальные значения m0 и H0 равны соответствующим параметрам априорного эллипсоида (4). В (7) и (8) γk, βk и введенные ωk – числовые параметры, в общем случае функционально связанные с переменными yk, uk, ck, mk-1, Hk-1. Способ вычисления этих параметров выделяет конкретный вид алгоритма эллипсоидов из рассматриваемого здесь класса. Предполагается, что для каждого из способов существуют такие константы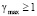 
и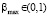 
, что для любых k
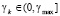, (9)
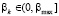. (10)
При этом для всего класса алгоритмов
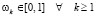. (11)
Из приведенных данных нетрудно найти, что
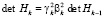, (12)
где det H – определитель матрицы H.
Пара (zk, yk) считается информативной, если
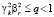, (13)
где q – некоторая константа. Поскольку объем эллипсоида Ek прямо пропорционален корню квадратному из определителя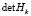 
матрицы Hk, то для информативных пар объемы эллипсоидов строго монотонно убывают.
Далее, будем рассматривать только информативные пары, считая, что условие (13) выполнено для всех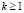 
.
В работе [4] были получены условия, налагаемые на вектор zk, при которых обеспечивалась сходимость оценок mk к оцениваемому вектору m*. Наличие ограничений (3) на вектор zk в общем случае не позволяет выполнить эти условия. В [8], например, показано, что в случае изменения вектора zk в одномерном подпространстве нельзя обеспечить сходимость оценок mk к вектору m*. В этом случае с течением времени происходит ортогонализация векторов zk и векторов невязки (m* – mk). Этот факт связан с тем, что уравнение (1) при отсутствии помех (ξk = 0) и при условии, что все zk принадлежат линейному одномерному пространству, имеет множество решений, представляет собой линейное многообразие размерности (n – 1), которое содержит вектор m* и для каждого его элемента m справедливо
.
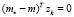Обозначим через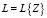 
минимальное линейное подпространство пространства Rn, содержащее множество Z. Пусть размерность этого подпространства равна m. Можно показать, что аналогичная картина возникает в том случае, когда векторы zk изменяются только в подпространстве L. В этом случае система уравнений (1) 
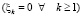также имеет не единственное решение, а множество решений, которое является линейным многообразием размерности (n – m). Это многообразие содержит вектор m* и для каждого его элемента m справедливо
.
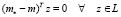Таким образом, в случае ограничений (3) требуется указать условия, налагаемые на векторы zk, при которых для последовательности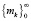 
оценок mk, генерируемых с помощью любого алгоритма из рассматриваемого класса, имел место предел
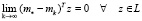. (14)
Условия сходимости
Подпространство L можно представить в следующем виде
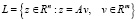, (15)
где столбцы (n×m) – матрицы А ортонормированны
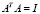. (16)
Здесь I – единичная (m×m) – матрица. Как следует из определения подпространства L, векторы-столбцы аi матрицы А представляют собой ортонормированный базис подпространства L. Получим оценку для величины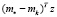 
, считая, что 
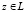. При этом учтем, что по построению эллипсоид Еk содержит вектор m*, а для вектора z справедливо представление 
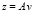. В результате получим
,
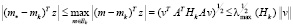где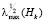 
– максимальное собственное значение матрицы Hk = ATHkA. Сформулированная выше задача будет решена, если на последовательности 
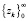будет иметь место предел
.
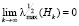Как следует из определения множества L, любой вектор zk представим в виде
.
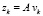где vk – некоторый вектор из Rm. Подставляя это выражение в равенство (7) и умножая его слева на AT и справа на A, получим
.
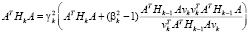Учитывая обозначение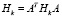 
,
последнее равенство можно переписать в виде
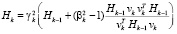. (17)
Нетрудно заметить, что это уравнение совпадает с уравнением (8) за исключением размерности и обозначения вектора vk.
Условия, при которых последовательность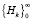 
матриц Hk, вычисляемых в соответствии с приведенным выше уравнением, стремится к нулевой матрице, получены в [4]. Для этого случая справедливо следующее утверждение.
Утверждение 1. Пусть ε – некоторое фиксированное положительное число, взятое из интервала (0,1), и последовательность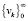 
такова, что выполняется условие
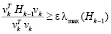. (18)
За исключением конечного числа моментов времени k. Тогда существует предел
.
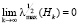Сформулированное утверждение представляет собой иную формулировку теоремы из [4], и его доказательство аналогично доказательству теоремы.
Условие (18) с учетом представления (17) и равенства (16) можно записать в следующем виде
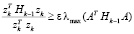. (19)
Заметим, что это условие не зависит от выбора матрицы А, фигурирующей в определении (15) подпространства L. Предположим, что в качестве матрицы А взята матрица В. Поскольку векторы-столбцы bi матрицы В также образуют ортонормированный базис подпространства L, то существует такая ортогональная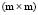 
-матрица S, что
.
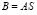Поэтому и в силу свойств собственных значений матрицы имеем
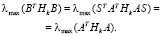
Покажем, что условие (19) можно выполнить при ограничении (3) на векторы zk. Условие (19) выделяет в пространстве Rn конус
.
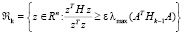Если для каждого момента времени k пересечение конуса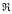 
и множества Z не пусто
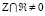. (20)
То существует последовательность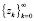 
векторов zk, удовлетворяющая условию (19) и ограничению (3) и на которой имеет место предел (14). Покажем, что можно выбрать число ε таким образом, что выполняется (20). Для этого введем следующие величины, характеризующие множество Z. Для любого единичного вектора 
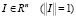будем рассматривать подпространство
,
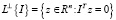ортогональное вектору I. Обозначим через
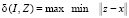
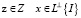
максимальное расстояние от множества Z до подпространства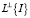 
. Поскольку
,
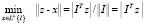то функция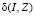 
приобретает вид
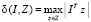. (21)
Функция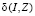 
обладает, в частности, следующими свойствами
.
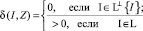Поскольку функция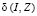 
непрерывна по I и вектор I изменяется в пределах компакта – единичной сферы, то она достигает своего минимального 
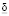и максимального 
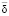значения при 
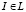. Причем 
.
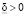Утверждение 2. Пусть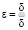 
. Тогда существует последовательность 
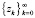векторов zk, удовлетворяющих как условию ограниченности (3), так и условию (19), на которой для каждого из алгоритмов рассматриваемого класса имеет место предел
.
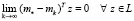Доказательство. Условие (19) получено из условия (18). Как показано в [4], условие (18) для векторов vk выполняется, если справедливо неравенство
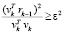, (22)
где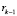 
– собственный вектор матрицы 
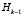, соответствующий максимальному собственному значению 
, 
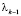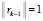. С учетом представления (17) и условия (16) неравенство (22) для векторов 
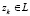эквивалентно следующему:
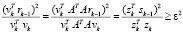. (23)
Заметим, что вектор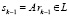 
и норма 
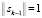. Предлагается в качестве элементов 
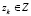искомой последовательности 
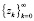брать аргументы решения следующей задачи
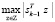. (24)
В этом случае получим, что
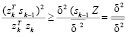. (25)
При получении последнего неравенства использовалась оценка сверху, для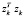 
, которая следует из следующего неравенства
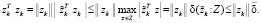
Таким образом из (25) следует, что если последовательность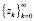 
определять при решении задачи (24), то условие (23) и, следовательно, условие (19) будет выполнено при 
.
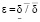Утверждение доказано.
В доказательстве утверждения содержится способ построения последовательности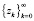 
, каждый вектор zk которой удовлетворяет условию ограниченности (3) и на которой обеспечивается сходимость рассматриваемого класса алгоритмов. Поскольку для произвольно заданной последовательности 
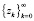условие (19) может не выполняться, то предлагается, так же как и в [4], преобразовывать элементы последовательности 
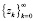по правилу
где ∆zk – изучающая добавка (для кратности – поправка) такая, что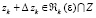 
.
Задача определения поправки ∆zk в общем случае имеет не единственное решение. То или иное ее решение может быть выбрано исходя из некоторых специфических дополнительных соображений. Например, наилучшее решение с точки зрения минимума нормы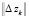 
может быть получено при взятии в качестве 
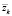проекции вектора zk на множество 
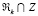. В силу произвольности множества Z определение этой проекции не является простой задачей.
Рассмотрим практически важный случай, при котором изучающие добавки ∆zk ограничены по норме
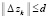. (26)
Здесь d – заданное положительное число. Рассмотрим множество
.
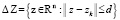Поскольку по условию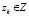 
, то множество 
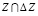никогда не пусто и является выпуклым и ограниченным как пересечение выпуклых и ограниченных множеств Z и ∆Z.
Лемма. При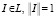 
функция 
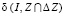достигает своего минимального 
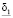и максимального 
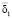значений, причем 
.
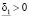Доказательство. Поскольку функция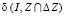 
непрерывна по I и вектор I изменяется в пределах единичной сферы, то она достигает своего минимального 
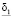и максимального 
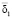значения при 
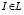. Покажем, что 
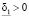. Предположим противное, т.е. пусть существует такой вектор 
, 
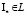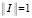, что функция 
.
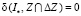Поскольку вектор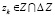 
,
то, используя определение функции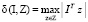 
, получим
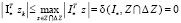. (27)
В то же время
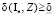> 0.
Пусть
.
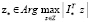Тогда
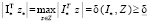> 0. (28)
Поскольку множество Z выпукло, то при любом значении числа γ, взятом из интервала [0,1], точка
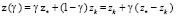
принадлежит множеству Z. Выберем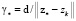 
.
Тогда точка
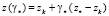
принадлежит множеству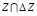 
. Для этой точки получаем
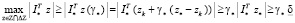> 0.
Последнее неравенство, полученное с учетом (27) и (28), противоречит предположению. Лемма доказана.
С помощью леммы достаточно просто можно доказать существование ограниченных по норме добавок ∆zk, обеспечивающих сходимость рассматриваемого семейства алгоритмов.
Утверждение 3. Пусть задана последовательность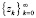 
векторов zk, удовлетворяющих условию ограниченности (3). Тогда существует такая последовательность 
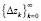векторов ∆zk, удовлетворяющих условию (26), что последовательность 
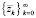векторов 
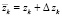удовлетворяет как условию ограниченности (3), так и условию (19) со значением параметра 
/
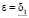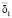и на которой для каждого из алгоритмов рассматриваемого класса имеет место предел
.
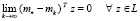Доказательство этого утверждения аналогично доказательству утверждения 2 с той лишь разницей, что максимум в (24) надо брать по множеству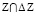 
. Тогда в соответствии с леммой условие сходимости (23) или (19) будет выполнено при значении параметра 
.
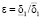В заключение приведен один из простейших алгоритмов вычисления изучающих добавок в случае, когда множество Z является многогранником.
Алгоритм построения изучающих добавок
Алгоритм вычисления изучающих добавок, когда множество Z – многогранник. Предположим, что множество Z задано как пересечение конечного числа многомерных полос
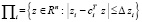
и является многогранником. В последнем выражении ci, числа zi и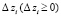 
предполагаются известными. Вычислим координаты вершин 
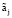многогранника Z с помощью алгоритма, приведенного в [9]. Затем определим максимальное количество m линейно независимых векторов 
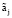и к этим векторам применим, например, процесс ортогонализации Грама – Шмидта. В результате определим базисные векторы ai подпространства L. Далее с помощью вычислительных методов линейной алгебры вычислим собственное значение 
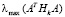и соответствующий собственный вектор 
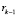матрицы 
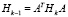. Проверим условие (19). Если оно выполнено, то вычисление добавки ∆zk не требуется. Если условие (19) не выполнено, то вычисляем вектор 
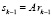и решаем задачу
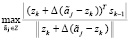. (29)
Здесь функция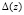 
определена следующим образом
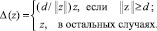
Задача (29) решается вместо более сложной
.
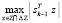В результате решения этой задачи определяется вектор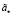 
, направленный в одну из вершин многогранника Z. Окончательно для вектора zk полагаем
.
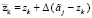Заметим, что в силу определения функции ∆(z) условие (26) ограниченности вектора добавок будет выполнено. После этого вычислим величину
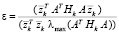
и полагаем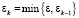 
.
В качестве начального условия для этого соотношения можно взять ε0 = 1. Можно показать, что при таком выборе εk его величина ограничена снизу
.
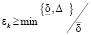В заключение заметим, что вычисления вершин многогранника и определение матрицы А выполняются не в режиме реального времени. Решение же задачи (29) при небольшой размерности не является трудоемкой задачей.
Численный пример
Рассмотрим задачу, оценивая для уравнения (1) при размерности n = 2. Вектор m* = (12, – 3). Априорная множественная оценка Е0 определялась параметрами m0 = (24, 0), H0 = diag(2500, 2500). Помеха ξk моделировалась с помощью генератора псевдослучайных чисел, равномерно распределенных в интервале [–20, 20]. Ограничения на значение вектора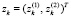 
были следующими:
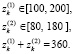
Исходная последовательность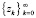 
была постоянной, 
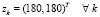. Таким образом, множество Z является отрезком и его концы задаются векторами 
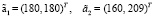. В данном случае матрица A = I и подпространство L совпадает с R2. Изучающие добавки построены в соответствии с алгоритмом, приведенным выше в статье. По результатам расчетов можно построить графики зависимости оценки 
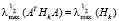для величины
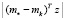от времени. Один график строят для величины d1 = 10, второй – для d2 = 1. Точность оценивания 0,25 была достигнута в первом случае на шаге k = 39, во втором на шаге k = 137. Таким образом, чем жестче ограничения на величину добавки, тем меньше скорость сходимости. Заметим, что при ∆ = 0 алгоритм может не сходиться.