В последние десятилетия исследования поведения жидкости в полостях твердых тел имеют широкое приложение к различным транспортным перевозкам жидких грузов, например, с помощью цистерн и нефтеналивных судов-танкеров. Кроме того, весьма актуальными представляются проблемы внутренних течений жидкого топлива на борту объектов ракетной и космической техники, влияние которого может быть весьма существенным из-за отсутствия при движении объекта, например, на орбите планеты, каких-либо точек опоры. Компенсационные мероприятия по предотвращению аварийных ситуаций, стабилизации траектории и режима движения объекта сопряжены с дополнительным расходом топлива, запасы которого на борту ограничены.
Исследования влияния жидкости на стенки сосудов и внутренние стабилизирующие устройства в виде кольцевых и радиальных перегородок также представляются достаточно актуальными с точки зрения определения эффективности силового воздействия на внутренние течения жидкости и минимально необходимой массы конструкций. Снижение суммарной массы внутренних устройств позволяет увеличить полезную нагрузку объекта, продолжительность полета объекта и надежность управления им в процессе орбитального полета.
Подобные задачи о внутренних течениях подразделяются на исследования в сосудах, частично заполненных идеальной жидкостью, которые имеют наибольшее распространение в большом массиве научной информации. Второй группой задач, менее многочисленной и исследованной недостаточно полно, представляются работы, посвященные изучению поведения вязкой несжимаемой жидкости, целиком заполняющей резервуары различной геометрии [1]. Такие течения имеют вид осесимметричных вращений жидкости вокруг одной или нескольких осей симметрии сосуда и отличаются меньшими силовыми воздействиями на стенки по сравнению с частично заполненными резервуарами. Такие воздействия, как правило, представляются силами или круговыми моментами вязкого трения жидкости о стенки и динамического влияния на внутренние перегородки [2].
Указанные воздействия могут являться причиной угловой неустойчивости объекта, отклонений от штатной программы полета и требуют компенсации со стороны системы стабилизации объекта. В случаях углового маневрирования объекта на орбите, например, для смены ориентации на Солнце или коррекции траектории движения, в автоматическую систему стабилизации необходимо вводить данные об условиях полета, что сопряжено с большими материальными затратами. Например, Национальным аэрокосмическим агентством (НАСА) США было выделено около 400 млн долларов для гидродинамических исследований поведения жидкого топлива на борту космического объекта учеными Юго-Западного исследовательского института (США) [3]. Однако представляется наиболее рациональным и эффективным проведение модельных исследований в наземных лабораторных условиях с учетом критериев подобия и распространением результатов на натурные условия и объекты.
Постановка задачи и средства моделирования
В лаборатории гидродинамики Дагестанского государственного технического университета были проведены комплексные гидродинамические исследования замкнутых течений жидкости на специально разработанной экспериментально аналитической базе. Комплекс средств включал в себя оригинальные конструкции экспериментальных стендов, методы моделирования, средства измерения и регистрации параметров течений, а также математические методы моделирования с помощью пакетов прикладных программ и численных методов решения уравнений движения жидкости [4, 5].
В настоящей статье предлагаются результаты математического моделирования течений в сферическом сосуде с помощью численного решения полных нестационарных уравнений движения вязкой несжимаемой жидкости в форме Навье – Стокса с соответствующими начальными и граничными условиями с помощью методов конечных объемов и конечных элементов. Постановкой математической задачи предполагались предварительный разгон вращения жесткой сферической оболочки, целиком заполненной вязкой несжимаемой жидкостью, до заданной угловой скорости и затем резкое торможение оболочки с одновременным исследованием нестационарного поля скоростей и давлений инерционного осесимметричного течения.
Согласно известным условиям моделирования осесимметричных течений рассматривалась половина продольного сечения сферы [4], а гипотеза о симметричности течения относительно экваториальной плоскости сосуда [5] позволяла рассматривать течения в масштабе квадранта сферы, что увеличивало вычислительный ресурс для решения подобной задачи. Таким образом, граничные условия для рассматриваемой задачи подразумевали равенство нулю скоростей жидкости на стенках и на вертикальной оси вращения сосуда.
Начальные условия задачи выражали твердотельное вращение жидкости согласно зависимости азимутальной (окружной) скорости u = Ω.R, где Ω – начальная угловая скорость сосуда; R – расстояние контрольной точки до оси вращения сосуда. Зависимость во времени течения согласно гипотезе Н.А. Слезкина [1] можно представить экспоненциальным рядом по убывающим степеням экспоненты
(*)
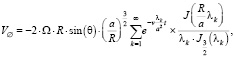где k – корни трансцендентного уравнения;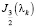 
– функции Бесселя 3/2 порядка; t – время затухания скорости жидкости.
В течении, описываемом равенством (*), необходимо учитывать особенности геометрии сосуда и отсутствие четко обозначенного перехода границ между верхней (нижней) и боковыми стенками, как это имеет место в цилиндре [6]. Возможные невязки граничных условий из-за взаимного влияния течений в соседних слоях могут обуславливать неустойчивость численной расчетной схемы, поэтому сферическая область разбивалась на более мелкие элементы порядка 295000 элементов. Основной трудностью при численном моделировании представлялось количественное определение скоростей вторичных циркуляционных течений в меридиональных плоскостях сферы, которые определяют картину течения в азимутальной плоскости сосуда.
В качестве основного инструмента для решения уравнений движения жидкости использовался лицензированный программный пакет АNSYS СFХ. Это позволило получить результаты распределения скоростей по всему объему сосуда в различные моменты времени нестационарного течения, а также линии тока для циркуляционных течений в меридиональных плоскостях, позволяющих установить структуру трехмерных течений и их влияние на формирование силовых воздействий со стороны жидкости на стенки сосуда.
Направление циркуляционных течений подтверждает гипотезы Х. Гринспена [1] о структуре и характере развития во времени вторичных течений в ограниченных объемах. Например, в экваториальной плоскости имеет место радиальное течение, направленное от оси вращения сферы к периферии сосуда, имеющее вид спирали с центром на оси вращения. В верхней и нижней областях сосуда, а также в области оси вращения формируются соответственно нисходящие и восходящие циркуляции, что подтверждает общую гипотезу о симметричности течения в сосуде при малых начальных угловых скоростях вращения оболочки. При возрастании чисел Рейнольдса, а соответственно, компонент вектора скорости условия симметрии относительно оси вращения, а также экваториальной плоскости сферы могут не соблюдаться. Проведенные автором экспериментальные измерения полей скорости течений позволили установить качественное, в пределах 27 %, соответствие экспериментальных и численных результатов распределения скоростей в экваториальной плоскости и меридиональных циркуляций [6].
На рис. 1 представлены результаты численного расчета течения в экваториальной плоскости сферы в сравнении с данными расчета профилей окружной скорости по Н.А. Слезкину [1], при малых числах Рейнольдса Rе = 920, когда достаточно велико влияние вязкой диффузии, а инерционные члены уравнений движения малы. Кроме того, можно наблюдать симметричность распределения окружной скорости с восходящим течением в левой части сечения сферы и ниспадающим – в правой, что соответствует результатам измерений в этой плоскости с помощью термоанемометрических датчиков скорости [6]. Формирование определенного направления циркуляционных течений обуславливается возникновением неравновесия между радиальным градиентом давления, центробежными силами инерции и кориолисовыми силами, которые могут вносить существенный вклад в дестабилизацию циркуляционного течения, являясь причиной дробления циркуляций на меньшие по масштабу структуры.
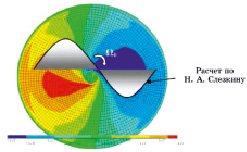
Рис. 1. Контурное изображение распределения окружной скорости на экваторе сферы при Rе0 = 920, полученное автором, в сравнении с результатами расчета уравнения (1) по Н.А. Слезкину (сплошная кривая)
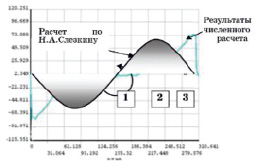
Рис. 2. Профили окружной скорости на экваторе сферы, полученные численным расчетом в сравнении с результатами Н.А. Слезкина (1) при Rе0 = 920
Результаты численного расчета позволили получить расчетные профили окружной скорости, которые представлены на рис. 2 в сравнении с данными вычислений по уравнению (*) из работы Н.А. Слезкина [1]. Анализ структуры профиля скорости позволил установить характерные зоны с твердотельным распределением скорости (зона 1), седловидным участком кривой (зона 2) и экстремумом скорости на границе с пристеночным заторможенным течением (зона 3). Указанные результаты имеют качественное сходство с данными экспериментальных измерений с погрешностью не более 20–23 % в исследованном диапазоне чисел Рейнольдса Rе = 700–12500.
Прямо пропорциональное увеличение окружной скорости и при возрастании расстояния R до оси вращения сосуда дополняется резким снижением скорости в пристеночной заторможенной области, характеризуя сильное влияние вязкой диффузии в течении. Верификация математической модели с помощью тестовых расчетов поля скоростей и давлений в экваториальной области цилиндра [6] свидетельствует о корректности разработанной математической модели и правильном выборе граничных условий для задачи о течении в сфере. По результатам численного моделирования течений и характеру изменения полей окружной скорости и скоростей вторичных течений можно составить зависимости сил и круговых моментов вязкого трения жидкости о стенки сосуда. Сопоставление численных данных с результатами экспериментальных исследований позволяет количественно оценить корректность математической модели течений и составить полную трехмерную картину нестационарного течения в сфере.
По аналогии с оценкой структуры вторичных течений при изменении времени затухания скорости в цилиндре на рис. 3 приведена эволюция циркуляций в сфере во времени, где показаны вторичные течения, состоящие из четырех циркуляций при Т = 2,34, которые затем, при Т = 12,7, преобразуются в двухциркуляционные структуры [5, 6]. Как видно из рисунка, циркуляционная система состоит из базовой циркуляции, центр которой располагается на координатах R = 0,78 и =/4, и трех более мелких структур (рис. 3, а и б), которые при Т = 10,7 объединяются в одну циркуляцию. При этом скорость течения в пределах базовой циркуляции затухает, однако ее ориентация в пространстве остается постоянной.
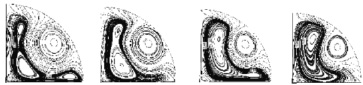
а) б) в) г)
Рис. 3. Слияние четырех циркуляций в две при возрастании времени затухания окружной скорости течения в сфере по результатам численного моделирования при Rео = 2500: а) Т = 2,34; б) 6,13; в) 10,7; г) 12,7
а) б) в) г) д)
Рис. 4. Слияние трех циркуляций в одну при возрастании времени затухания окружной скорости течения по результатам численного моделирования при Rе0 = 2150: а) Т = 1,57; б) 3,64; в) 7,67; г) 11,2; д) 15,3
В качестве еще одного примера эволюции циркуляций во времени в сфере можно привести результаты численного расчета при Rе = 2150, приведенные на рис. 4, где в начале течения возникает устойчивая трехциркуляционная структура (рис. 4, а). При возрастании времени Т = 7,67 она трансформируется в двухциркуляционную, которая существует до безразмерного времени Т = 11,2, а при достаточно больших значениях Т = 15,3 представляет собой одну циркуляцию. В данном случае базовая циркуляция располагается в экваториальной области сферы и только при больших значениях времени становится преобладающей во всем пространстве квадранта.
При числах Рейнольдса Rе = 3750 переход к двухэлементной циркуляции происходит примерно в таком же диапазоне окружных скоростей, что и течение, представленное на рис. 4, однако оси циркуляций ориентированы вертикально. В свою очередь, переход к базовой циркуляции осуществляется при больших значениях безразмерного времени Т = 15,3, когда инерционные члены уравнений движения жидкости весьма малы и преобладают силы вязкого трения [6].
Как видно из рис. 3 и 4, наиболее устойчивая циркуляция располагается на радиальной координате R = 0,7 – 0,85 при меридиональном угле = 40–47o (рис. 3 и 4, а–г), которая благодаря вязкой диффузии существует достаточно долго и теряет свою энергию лишь в заключительной стадии течения. При этом более мелкие разноориентированные циркуляционные структуры, в которые вовлечены приосевые и азимутальные течения, обладают меньшим количеством движения, однако более активно участвуют в перераспределении структуры меридионального течения.
Различные гипотезы о фактической неосесимметричности подобных круговых течений и слабой симметричности относительно азимутальной плоскости сферы имеют право на существование, однако нуждаются в экспериментальном и аналитическом подтверждении. Это сопряжено с необходимостью решения трехмерных нестационарных задач с учетом большого количества факторов, моделирование которых в настоящее время находится в стадии разработки. Однако приведенные осесимметричные численные решения нестационарной задачи позволяют качественно оценить и представить характер развития гидродинамической картины течения в сферическом сосуде и создать информационную базу для разработки трехмерных математических моделей течений в ограниченных объемах.
Выводы
Эволюция циркуляционных течений в меридиональных плоскостях во времени свидетельствует об их существенном влиянии на картину распределения окружной скорости в сфере. Это, в свою очередь, позволяет количественно определить силовые влияния жидкости на стенки и установить направление этих воздействий на конструкцию сосуда. Кроме того, зависимости величин скорости от времени течения позволяют проследить экспоненциальный характер изменения силовых воздействий во времени, что подтверждает предложенные Н.А. Слезкиным аналитические оценки характера затухания азимутальной скорости течения.
Таким образом, вклад сил вязкого трения в суммарное силовое воздействие течения на стенки сосуда можно учитывать при разработке компьютерных программ для автоматической системы стабилизации, например, космического аппарата. Это позволит учитывать инерционное влияние жидкости при выполнении компенсационных, коррекционных и ориентационных разворотов объекта, что позволит экономить жидкое топливо. Для наземного и морского транспорта, содержащего большие количества жидкости, подобные возмущения не являются критическими, однако их следует учитывать при проектировании цистерн и танков нефтеналивных судов.