Уникальные свойства бозе-эйнштейновских конденсатов (БЭК) привлекают значительный интерес в последние десятилетия. Использование резонанса Фешбаха [1], перестраиваемых оптических решеток [2], атомных чипов [3] и т.д. делают БЭК привлекательным объектом для теоретических и экспериментальных исследований в физике многих частиц, создающим базис для развития новых технологий. Новые приложения требуют углубленного понимания нелинейной динамики конденсатов. Наиболее интересной теоретической проблемой является динамика частиц в ангармонических потенциалах (потенциальные «ямы») описывающие квантовые осцилляторы. В данной работе мы предлагаем метод возбуждения квазиодномерного конденсата, захваченного в ангармонической ловушке с основного состояния до высоких энергий в квазиклассическом приближении. Основная идея метода состоит в накачке конденсата возмущениями поля с медленно изменяющейся частотой с использованием идеи авторезонанса. В классическом варианте авторезонансное возбуждение осцилляторов рассматривалось еще в классических работах Векслера и Мак-Миллана [4, 5] и связано с эффектом «захвата» фазы осциллятора внешним переменным полем. В настоящее время авторезонанс имеет приложения в таких различных областях, как гидродинамика [6], физика плазмы [7], магнетизм [8], нелинейная оптика [9] и др. Авторезонанс в БЭК был впервые изучен в [10] случае осциллирующей длины рассеяния. Возбуждение БЭК от основного состояния к первому возбужденному уровню с использованием метода оптимального управления исследовано экспериментально в работе [11].
В данной работе исследование авторезонансного возбуждения проводится в рамках уравнения Гросса – Питаевского
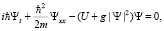 (1)
(1)
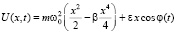 , (2)
, (2)
где параметр ангармоничности β > 0. Последний член в уравнении (2) является малым возмущением потенциала с частотой 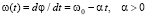 , медленно уменьшающейся со временем и проходящей через линейную резонансную частоту ω0 при t = 0. Мы предполагаем, что волновая функция нормализована на единицу и, таким образом, параметр g будет пропорционален полному числу частиц в конденсате. Как классический, так и квантовый авторезонанс в линейном аналоге (g = 0) уравнения (1) изучался в работе [12]. В данной работе мы сосредоточим внимание на нелинейных эффектах из-за взаимодействия частиц конденсата и дадим новый взгляд на квазиклассические эффекты этого взаимодействия, охватывающие случай большого числа частиц в конденсате, представляющий наибольший интерес с экспериментальной точки зрения.
, медленно уменьшающейся со временем и проходящей через линейную резонансную частоту ω0 при t = 0. Мы предполагаем, что волновая функция нормализована на единицу и, таким образом, параметр g будет пропорционален полному числу частиц в конденсате. Как классический, так и квантовый авторезонанс в линейном аналоге (g = 0) уравнения (1) изучался в работе [12]. В данной работе мы сосредоточим внимание на нелинейных эффектах из-за взаимодействия частиц конденсата и дадим новый взгляд на квазиклассические эффекты этого взаимодействия, охватывающие случай большого числа частиц в конденсате, представляющий наибольший интерес с экспериментальной точки зрения.
Результаты исследования и их обсуждение
Используем обозначения статьи [12] для согласования с линейным случаем. Различные динамические режимы в уравнении (1) будем ассоциировать с параметрами P1, P2, использованными в работе [12], и введем новый параметр P3, определяющий влияние нелинейности. Эти параметры конструируются из четырех характерных времен задачи: время, обратное частоте Раби 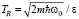 , время изменения частоты
, время изменения частоты 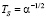 , характерный временной масштаб ангармоничности
, характерный временной масштаб ангармоничности 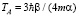 и нелинейности
и нелинейности 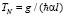 , где
, где 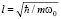 есть характерная длина для ангармонического осциллятора. Окончательно безразмерные параметры определяются следующими формулами
есть характерная длина для ангармонического осциллятора. Окончательно безразмерные параметры определяются следующими формулами
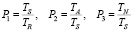 , (3)
, (3)
которые измеряют величину накачки, ангармоничность и нелинейность соответственно.
Вводя безразмерные координату ξ = x/l, время T = ω0t, скорость изменения частоты 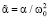 и волновую функцию
и волновую функцию 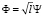 , перепишем уравнения (1), (2) в виде
, перепишем уравнения (1), (2) в виде
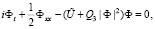 (4)
(4)
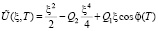 , (5)
, (5)
где 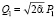 ,
, 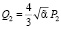 ,
, 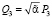 и
и 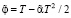 . В дальнейшем мы будем ограничиваться только случаем положительной нелинейности P3 > 0.
. В дальнейшем мы будем ограничиваться только случаем положительной нелинейности P3 > 0.
В работе [13] было показано, что в динамической системе (4), (5) квазиклассический режим реализуется при
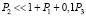 , (6)
, (6)
т.е. когда ангармоничность является достаточно слабой. Кроме того, численные исследования показывают необычное поведение функции вероятности перехода системы из основного в возбужденное состояние при авторезонансной накачке. Эта зависимость приведена на рисунке. Хорошо видно быстрое уменьшение ширины области перехода с ростом нелинейности так, что уже при P3 > 20 функция перехода стремится к ступенчатой функции. Этот результат является принципиальным для возможных приложений авторезонансных переходов для целей диагностики и создания высокоточных детекторов. В отличие от линейного случая (отсутствие взаимодействия между частицами) [12], разрешение таких детекторов не ограничивается квантовыми флуктуациями если взаимодействие между частицами достаточно велико (6). Ниже мы дадим теоретическую интерпретацию этого важного эффекта уменьшения ширины перехода в квазиклассическом случае.
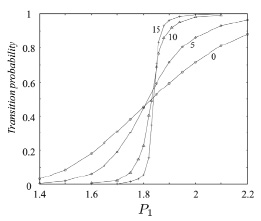
Зависимость вероятности перехода от величины накачки P1 для P2 = 0,2 и P3 = 0,5; 10; 15
Для описания квазиклассического состояния конденсата запишем волновую функцию в виде волнового пакета [14]
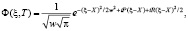 (7)
(7)
где X(T) – координата центра масс конденсата, w(T) – характерная ширина волнового пакета, P(T), R(T) – соответствующие импульсы. В начальный момент времени, когда конденсат находится в основном состоянии, параметры волновой функции имеют значения X = P = R = 0, w = 1. Дальнейшая эволюция этих параметров может быть определена с помощью вариационного принципа. Для этого подставим волновую функцию (7) в плотность лагранжиана для уравнения (4) и проинтегрируем по пространственной координате. В результате получим эффективную функцию Лагранжа, из которой следуют вариационные уравнения для X и w
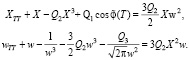 (8)
(8)
Прочие параметры могут быть найдены из соотношений 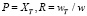 . Уравнения (8) описывают пару нелинейных осцилляторов, связанных посредством слагаемых в правой части. Согласно уравнению (6) параметр
. Уравнения (8) описывают пару нелинейных осцилляторов, связанных посредством слагаемых в правой части. Согласно уравнению (6) параметр 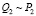 является малым в области квазиклассической динамики, поэтому осцилляторы (8) связаны весьма слабо. Однако даже эта слабая связь будет существенно влиять на динамику системы, если между колебаниями координаты центра масс и ширины волнового пакета возможен резонанс. Оценим собственные частоты колебаний этих величин. Уравнение для координаты X(T) центра масс волнового пакета представляет собой возмущенное уравнение Дюффинга. Решение этого уравнения можно представить в виде
является малым в области квазиклассической динамики, поэтому осцилляторы (8) связаны весьма слабо. Однако даже эта слабая связь будет существенно влиять на динамику системы, если между колебаниями координаты центра масс и ширины волнового пакета возможен резонанс. Оценим собственные частоты колебаний этих величин. Уравнение для координаты X(T) центра масс волнового пакета представляет собой возмущенное уравнение Дюффинга. Решение этого уравнения можно представить в виде 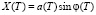 , причем частота слабонелинейных колебаний этой величины имеет вид [15]
, причем частота слабонелинейных колебаний этой величины имеет вид [15] 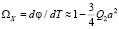 . Известно, что при медленном переходе частоты накачки
. Известно, что при медленном переходе частоты накачки 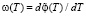 через линейный резонанс в уравнении Дюффинга возможен эффект авторезонанса, при котором происходит непрерывный рост энергии (и амплитуды) колебаний, несмотря на изменение частоты накачки [15]. В терминах параметров Pi необходимое условие существования авторезонанса имеет вид
через линейный резонанс в уравнении Дюффинга возможен эффект авторезонанса, при котором происходит непрерывный рост энергии (и амплитуды) колебаний, несмотря на изменение частоты накачки [15]. В терминах параметров Pi необходимое условие существования авторезонанса имеет вид 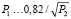 . В режиме авторезонанса частота колебаний остается близкой к частоте накачки, а амплитуда a(T) медленно меняется со временем. Если авторезонанса в системе нет, то при переходе через линейный резонанс происходит лишь малый скачок амплитуды
. В режиме авторезонанса частота колебаний остается близкой к частоте накачки, а амплитуда a(T) медленно меняется со временем. Если авторезонанса в системе нет, то при переходе через линейный резонанс происходит лишь малый скачок амплитуды 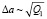 , известный как рассеяние на резонансе [16]. Чтобы найти собственную частоту колебаний ширины волнового пакета w(T), представим эту величину в виде
, известный как рассеяние на резонансе [16]. Чтобы найти собственную частоту колебаний ширины волнового пакета w(T), представим эту величину в виде 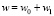 , где w0 – медленно меняющееся среднее значение, удовлетворяющее уравнению
, где w0 – медленно меняющееся среднее значение, удовлетворяющее уравнению
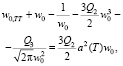
а w1 – малое отклонение. Линеаризованное уравнение для w1 имеет вид
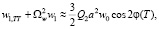 (9)
(9)
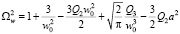 .
.
В случае линейного гармонического осциллятора Q2 = Q3 = 0 (одна частица в гармонической ловушке) получаем w0 = 1, поэтому собственная частота равна 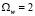 . При малых значениях Q2 и Q3 будем по-прежнему иметь
. При малых значениях Q2 и Q3 будем по-прежнему иметь 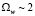 . Заметим, что вынуждающая сила в правой части уравнения (9) совершает колебания с частотой
. Заметим, что вынуждающая сила в правой части уравнения (9) совершает колебания с частотой 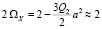 , так как мы рассматриваем случай, когда параметр Q2 мал. Таким образом, при малых значениях Q2 и Q3 собственная частота осциллятора (9) и частота вынуждающей силы в его правой части оказываются близкими, что приводит к резонансному усилению колебаний w(T). Иными словами, ширина волнового пакета начинает совершать колебания с быстро растущей амплитудой, что можно интерпретировать как неустойчивость такого волнового пакета, приводящую в исходной системе (4) к распаду решения вида (7). Увеличение нелинейности Q3 приводит к смещению частоты
, так как мы рассматриваем случай, когда параметр Q2 мал. Таким образом, при малых значениях Q2 и Q3 собственная частота осциллятора (9) и частота вынуждающей силы в его правой части оказываются близкими, что приводит к резонансному усилению колебаний w(T). Иными словами, ширина волнового пакета начинает совершать колебания с быстро растущей амплитудой, что можно интерпретировать как неустойчивость такого волнового пакета, приводящую в исходной системе (4) к распаду решения вида (7). Увеличение нелинейности Q3 приводит к смещению частоты 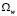 и нарушению резонансного соотношения
и нарушению резонансного соотношения 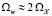 , поэтому при большой нелинейности решение (7) оказывается устойчивым. Это означает, что если в уравнении Дюффинга для координаты волнового пакета происходит авторезонанс, то весь волновой пакет как целое совершает колебания, амплитуда которых увеличивается по мере уменьшения частоты накачки. Вероятность захвата в авторезонанс в исходной системе (4) в этом случае близка к единице. Таким образом, с увеличением числа частиц в БЭК, вероятность захвата фазы как функция от амплитуды накачки стремится к ступенчатой функции, характерной для классического маятника Дюффинга (рисунок). Так как Q3 не входит в первое уравнение (8), положение фронта этой функции не зависит от нелинейности и совпадает с классическим порогом авторезонанса [15]:
, поэтому при большой нелинейности решение (7) оказывается устойчивым. Это означает, что если в уравнении Дюффинга для координаты волнового пакета происходит авторезонанс, то весь волновой пакет как целое совершает колебания, амплитуда которых увеличивается по мере уменьшения частоты накачки. Вероятность захвата в авторезонанс в исходной системе (4) в этом случае близка к единице. Таким образом, с увеличением числа частиц в БЭК, вероятность захвата фазы как функция от амплитуды накачки стремится к ступенчатой функции, характерной для классического маятника Дюффинга (рисунок). Так как Q3 не входит в первое уравнение (8), положение фронта этой функции не зависит от нелинейности и совпадает с классическим порогом авторезонанса [15]: 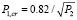 , что также хорошо видно на рисунке.
, что также хорошо видно на рисунке.
Выводы
В данной работе мы показали, что важный эффект сужения функции вероятности перехода при авторезонансной накачке, обусловленный взаимодействием частиц конденсата, определяется нелинейным сдвигом резонансных частот. Этот сдвиг увеличивается с числом частиц конденсата, обеспечивая устойчивость авторезонансного захвата фазы. В силу этого авторезонанс развивается более эффективно, приводя к резкому сужению области перехода.
Работа выполнена в рамках проекта УрО РАН № 15-8-2-7 «Локализованные структуры, солитоны и их возбуждение в конденсированных средах».

