Бесщелевой полупроводник HgSe, содержащий примеси 3d-переходных металлов, относится к системам, в которых примесные 3d-состояния гибридизуются с зонными состояниями невозмущенного кристалла [1]. Подобные системы вызывают в последние годы интерес для исследования [2–4]. Следствием гибридизации примесных и свободных электронных состояний является теоретически предсказанная спонтанная спиновая поляризация электронов [5]. Этот эффект был подтвержден экспериментально посредством наблюдения аномального эффекта Холла (АЭХ) в монокристаллах HgSe, легированных примесями (Fe, V, Ni, Cr и Co), при комнатной температуре [6]. Соединения HgSe:3d мы будем называть слабыми магнетиками, ввиду малой ~ (0,01 – 0,1) ат. % концентрации магнитной 3d-примеси. Теоретическое описание АЭХ, обнаруженного в слабых магнетиках, представлено в работах [6, 7]. Показано, что в основе АЭХ лежит термодинамическая природа, которая отражает свойства локального термодинамического равновесия электронной системы. Эта особенность отличает термодинамический АЭХ от наиболее распространенного АЭХ, обусловленного спин-орбитальным взаимодействием в магнитных материалах [8–10]. Основой термодинамического механизма АЭХ в системах со спонтанной намагниченностью является возбуждение электрическим полем тока спонтанного намагничения, следствием чего согласно [6, 7] является появление в локально равновесном токе проводимости некоторой магнитной составляющей, равной по величине току намагничения. Именно эта добавка в холловском токе проводимости описывает в конечном итоге термодинамический АЭХ. Поэтому обнаружение в холловском токе проявлений термодинамических токов намагничения явилось бы наглядным и весомым аргументом в пользу существования спонтанной спиновой поляризации в слабых магнетиках на основе селенида ртути. Данная работа в идейном плане продолжает нашу работу [11] и дополняет ее экспериментальными данными при температуре жидкого азота.
Материалы и методы исследования
Ранее исследования АЭХ в слабомагнитных кристаллах на основе HgSe уже проводились [6]. Отличие предложенного в данной работе метода исследования эффекта Холла от распространенного метода для постоянного тока и магнитного поля [12] заключается в измерении тока, протекающего во вторичной цепи (рис. 1, а), сопротивление которой можно считать достаточно малым RC << RB. Принципиальная схема, использованная нами в измерениях, представлена на рис. 1, а. В данной схеме цепь 1 является высокоомной, ток I в которой практически не изменяется с приложением магнитного поля. Цепь 2 является низкоомной цепью, ток I0 в которой (далее, «ток отражения») согласно правилу Кирхгофа выражается как I0 = I – IS, где IS – ток через образец. В реальных образцах ток отражения будет обладать смешанной четностью по магнитному полю, поскольку будет содержать как четный вклад от магнитосопротивления, так и нечетный вклад от холловского сопротивления, который возникает из-за вызванной неоднородностью распределения концентрации носителей тока разности эдс Холла вблизи противоположных токовых контактов. Эту разность эдс, которая приводит к нечетной по напряженности магнитного поля добавке (∆I0)odd к току отражения, можно выразить как ∆V = (V1+ – V2–) – (V3+ – V4–) = (V1+ – V3+) – (V2– – V4–) (рис. 1, а). Иначе говоря, вклад (∆I0)odd может быть выражен как разница между холловскими токами 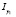 и
и 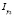 , возникающими из-за шунтирования образца токовыми контактами вблизи торцов [12]. Поэтому представленный метод мы назвали дифференциальным методом тока Холла.
, возникающими из-за шунтирования образца токовыми контактами вблизи торцов [12]. Поэтому представленный метод мы назвали дифференциальным методом тока Холла.
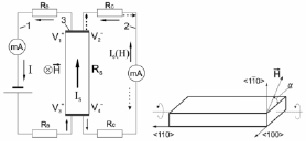
а) б)
Рис. 1. (a) – Принципиальная схема для иллюстрации дифференциального метода тока Холла: 1 – высокоомная цепь с RB ~ 103 Ом; сопротивление образца RS ~ 10–2 Ом; 2 – вторичная низкоомная цепь с RC ~ 1; 3 – токовый электрод. (б) – Геометрия образцов с указанием кристаллографических направлений и оси вращения
Параметры образцов HgSe:Co и HgSe:Ga при Т = 300 К
|
№ |
Примесь |
Концентрация примеси, см-3 |
ne·1018, см-3 |
σ0·104, Ом-1·см-1 |
μH·104, см2/В·с |
I, мA |
|
1 |
Со |
6·1017 |
1,24 |
0,24 |
1,19 |
70 |
|
2 |
Со |
1,5·1018 |
0,56 |
0,15 |
1,62 |
60 |
|
3 |
Со |
4·1018 |
0,88 |
0,20 |
1,40 |
70 |
|
4 |
Со |
7·1018 |
0,57 |
0,15 |
1,66 |
60 |
|
5 |
Ga |
5,5·1018 |
5,6 |
0,6 |
0,67 |
80 |
Используя предложенный метод возможно, помимо изучения поведения тока Холла, также оценить степень однородности образца. Для демонстрации этого утверждения приведем выражение для холловского тока в следующем виде [6]:
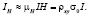 (1)
(1)
Здесь μH = RHσ0 – подвижность носителей, ρxy = RHH – сопротивление Холла, σ0 – проводимость в нулевом магнитном поле. При получении (1) сделано предположение, что Iобр ≈ I, а сам образец достаточно длинный и изотропный [12]. Тогда разность токов Холла вблизи торцов выражается как
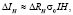 (2)
(2)
где 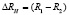 , R1 и R2 – коэффициенты Холла соответственно на противоположных концах образца. Тогда на основе (2) можно ввести параметр относительной неоднородности образца следующим образом:
, R1 и R2 – коэффициенты Холла соответственно на противоположных концах образца. Тогда на основе (2) можно ввести параметр относительной неоднородности образца следующим образом:
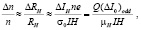 (3)
(3)
где 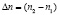 , n – средняя по объему образца электронная концентрация. В выражении (3) сделано предположение, что разность ∆IH и нечетный вклад (∆I0)odd, являющийся частью ∆IH, связаны линейной зависимостью через коэффициент Q. Пусть образец является низкоомным, то есть R⊥ << RC, где R⊥ – сопротивление образца в направлении холловского тока. В этом предельном случае следует предположить, что Q ~ σ0. Тогда с помощью (3) для i-го и j-го образца из совокупности образцов с близкой геометрией можно ввести важную для аттестации образцов характеристику – отношение параметров неоднородности:
, n – средняя по объему образца электронная концентрация. В выражении (3) сделано предположение, что разность ∆IH и нечетный вклад (∆I0)odd, являющийся частью ∆IH, связаны линейной зависимостью через коэффициент Q. Пусть образец является низкоомным, то есть R⊥ << RC, где R⊥ – сопротивление образца в направлении холловского тока. В этом предельном случае следует предположить, что Q ~ σ0. Тогда с помощью (3) для i-го и j-го образца из совокупности образцов с близкой геометрией можно ввести важную для аттестации образцов характеристику – отношение параметров неоднородности:
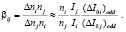 (4)
(4)
Целью настоящей работы являлось изучение особенностей поведения холловского тока в слабых магнетиках на основе селенида ртути и получения информации о степени однородности образцов путем выделения нечетной компоненты в угловой и магнитополевой зависимости тока отражения. Эксперимент был выполнен при температурах 77 и 300 К.
Образец вращался в магнитном поле величиной до 25 кЭ, создаваемом электромагнитом, таким образом, что ось вращения совпадала с направлением электрического тока, а магнитное поле было ему перпендикулярным. Угол вращения α отсчитывался от широкой грани образца (рис. 1, б), изменяясь 0 до 180 ° в магнитном поле сначала условно положительного направления (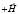 ), а затем – отрицательного направления (
), а затем – отрицательного направления (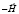 ). В последнем случае уголу поворота приписывались отрицательные значения. Очевидно, что такое поэтапное вращение эквивалентно повороту образца от 0 до 360 ° при фиксированном направлении магнитного поля.
). В последнем случае уголу поворота приписывались отрицательные значения. Очевидно, что такое поэтапное вращение эквивалентно повороту образца от 0 до 360 ° при фиксированном направлении магнитного поля.
В качестве легирующей магнитной примеси в настоящей работе использовался кобальт. Кроме образцов HgSe:Со, которые были ориентированными (рис. 1, б), исследовался специально неориентированный образец HgSe, содержащий немагнитную примесь Ga. Все образцы вырезались из наиболее однородной – средней части монокристаллических слитков, выращенных методом Бриджмена Подготовка образцов к измерениям проводилась путем шлифовки, полировки и травлении в 5 % растворе брома в изобутиловом спирте. Для изготовления омических токовых электродов использовалась амальгама галлия и серебра Образцы имели форму прямоугольного параллелепипеда с сечением ≈ 1×2 мм2 и длиной ≈ 8–10 мм. Нумерация образцов, их основные физические параметры при T = 300 K и значения тока I для первичной цепи приведены в таблице. Все измерения проводились при коммутации тока через образец. Величина тока I0 в зависимости от сопротивления образца варьировалась в интервале ≈300–500 мкА. На рис. 1, б приведен вариант кристаллографических направлений, реализованный в образцах 1–3. Для образца 4 направления <100> и 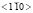 менялись местами. Отметим, что величина холловской подвижности μH = RHσ0 при температурах эксперимента 77 и 300 К для образцов 1–5 хорошо согласуется с полученной разными авторами в кристаллах HgSe зависимостью подвижности от концентрации электронов ne [13, 14]. Этот факт можно рассматривать как свидетельство соответствия качества исследуемых образцов мировому уровню.
менялись местами. Отметим, что величина холловской подвижности μH = RHσ0 при температурах эксперимента 77 и 300 К для образцов 1–5 хорошо согласуется с полученной разными авторами в кристаллах HgSe зависимостью подвижности от концентрации электронов ne [13, 14]. Этот факт можно рассматривать как свидетельство соответствия качества исследуемых образцов мировому уровню.
Результаты исследования и их обсуждение
Зависимость тока отражения IH = I0 + ∆I0(H) от угла поворота α, полученная в магнитном поле H = 20 кЭ, показана на рис. 2 для образцов 2 и 3. Здесь ∆I0(H) – добавка к току отражения в магнитном поле. Как видно, изменение знака α проявляет нечетный вклад (∆I0)odd в угловую зависимость тока IH. Именно она является ответственной за поведение разности токов Холла. Зависимость искомой нечетной компоненты (∆I0)odd от α при повороте от 0 до 360 ° приведена на рис. 3. Как показывают представленные на этом рисунке данные, понижение температуры от 300 до 77 К не влияет на характер угловой зависимости (∆I0)odd. Ее для исследованных образцов можно представить в виде эмпирического закона (∆I0)odd = Asin(α + φ0) = asinα + bcosα, где 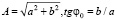 . Представление (∆I0)odd в виде суммы синуса и косинуса отражает протекание холловского тока при закорачивании сплошным токовым электродом попарно узких и широких боковых граней образца. Это связано соответственно с перпендикулярной (α = 90 °) и параллельной (α = 0 °) компонентами напряженности магнитного поля. Отсюда следует, что обнаруженная на эксперименте угловая зависимость нечетной компоненты тока отражения в образцах HgSe:Co и HgSe:Ga (рис. 3) связана не только со спецификой спонтанной спиновой поляризации в слабом магнетике, но также с неоднородным распределением концентрации электронов в образце.
. Представление (∆I0)odd в виде суммы синуса и косинуса отражает протекание холловского тока при закорачивании сплошным токовым электродом попарно узких и широких боковых граней образца. Это связано соответственно с перпендикулярной (α = 90 °) и параллельной (α = 0 °) компонентами напряженности магнитного поля. Отсюда следует, что обнаруженная на эксперименте угловая зависимость нечетной компоненты тока отражения в образцах HgSe:Co и HgSe:Ga (рис. 3) связана не только со спецификой спонтанной спиновой поляризации в слабом магнетике, но также с неоднородным распределением концентрации электронов в образце.
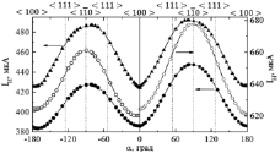
Рис. 2. Зависимость тока отражения IH от угла поворота α для образца 2 (○) и 3 (●, ▲) при температуре: 77 К (▲) и 300 К (○, ●). Верхняя шкала здесь и на рис. 3 показывает кристаллографические направления
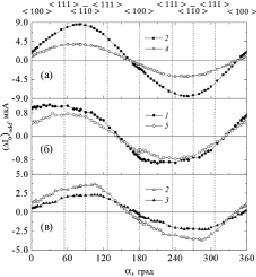
Рис. 3. Угловая зависимость нечетного вклада в ток отражения (∆I0)odd в магнитном поле 20 кЭ при Т = 300 К (панели a и б) и 77 К (панель в). Номера кривых совпадают с номерами образцов в таблице
Полученные угловые характеристики компоненты (∆I0)odd позволяют провести исследование ее магнитополевой зависимости для угла поворота образца, при котором величина эффекта максимальна. Типичная зависимость ∆I0(H) = IH – I0, иллюстрирующая наличие нечетного вклада в ток отражения, показана на вставке к рис. 4 на примере образца 3 при α = 90 °. Зависимость нечетной составляющей (∆I0)odd от магнитного поля для исследованных образцов представлена на рис. 4 и 5. Из рис. 5 видно, что для образца HgSe:Ga, который не является слабым магнетиком, зависимость (∆I0)odd от магнитного поля близка к линейной (сплошная прямая на рис. 5). Очевидно, что угол наклона этой прямой отражает различие в величинах электронных концентраций вблизи двух токовых электродов. Для образцов HgSe:Со, в которых реализуется АЭХ, характер магнитополевой зависимости (∆I0)odd меняется. Она является нелинейной в сравнительно низких магнитных полях и имеет линейный характер при дальнейшем увеличении магнитного поля (пунктирные прямые на рис. 4, 5). Полученный результат имеет два важных аспекта.
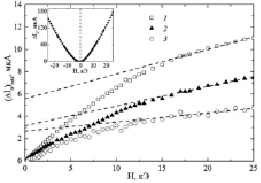
Рис. 4. Зависимость нечетного вклада в ток отражения (∆I0)odd от магнитного поля для образца 2 (кривые 1, 3) и 3 (кривая 2). Значения температур: 300 К (кривые 1, 2) и 77 К (кривая 3). Кривая 2 получена при α = 60 °, кривые 1, 3 – при α = 90 °. Пунктирные линии – экстраполяция экспериментальных кривых линейной функцией в области высоких магнитных полей. На вставке: магнитополевая зависимость изменения полного тока отражения ∆I0(H) для образца 3 при Т = 300 К и α = 90 °
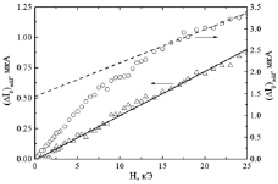
Рис. 5. Зависимость нечетного вклада в ток отражения (∆I0)odd от магнитного поля для образца 4 (○) и 5 (∆) при Т = 300 К. Пунктирная линия – экстраполяция экспериментальной зависимости для образца 4 линейной функцией в области высоких магнитных полей. Сплошная прямая – подгонка данных для образца 5 линейной функцией
Во-первых, он указывает на наличие аномального вклада в разности токов Холла, который насыщается с ростом Н так же как выявленный ранее аномальный вклад в холловское напряжение [6]. Можно дать следующую качественную интерпретацию этой особенности. Согласно теории [6, 7] электрическое поле E, приложенное к системе поляризованных по спину электронов приводит в магнитном поле к возбуждению тока спонтанного намагничения
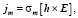 (5)
(5)
где h = H/H – единичный вектор. Оказывается, что кроме зависимости от магнитного и электрического поля ток спонтанного намагничения согласно (5) определяется параметром σm, который имеет размерность проводимости. Этому параметру, характеризующему спонтанную намагниченность, можно придать смысл магнитной проводимости [7]. При этом ток спонтанного намагничения приводит, в свою очередь, к добавлению в холловском токе проводимости к обычному недиссипативному члену «аномального» слагаемого – магнитной части локально равновесного тока, которая равна во величине и противоположна по знаку току jm [7]. Таким образом, в эксперименте (рис. 4, 5) обнаружено насыщение аномального вклада в дифференциальный ток (∆I0)odd с ростом магнитного поля. Для образцов HgSe:Со его можно связать с насыщением тока спонтанного намагничения (5), отражающего насыщение спонтанной намагниченности поляризованных по спину электронов через параметр σm.
Во-вторых, линейная магнитополевая зависимость дифференциального тока (∆I0)odd в области высоких магнитных полей (рис. 4, 5) свидетельствует о неоднородном распределении концентрации носителей тока в исследованных образцах. Продемонстрируем, как по формуле (4) оценить отношение параметров неоднородности βij при α = 90 °. Рассмотрим в качестве примера образцы с номерами (3–5). После вычета аномального вклада из соответствующих зависимостей на рис. 4 и 5 для образцов 3 и 4 получим в поле Н = 20 кЭ (∆I0)odd ≈ 5,4 и 1,9 мкА соответственно. Для образца 5 величина (∆I0)odd заметно меньше и составляет в таком же поле ≈0,9 мкА, что следует из рис. 3, б (кривая 5). Подставив из таблицы параметры I и n в формулу (4), найдем: β34 = 3,8, β35 = 1,08, β54 = 3,5. Таким образом, согласно критерию (4) наиболее однородным из трех аттестуемых образцов является образец 4, а самым неоднородным – образец 3.
Заключение
В рамках общего подхода, основанного на исследовании образцов HgSe:Со методом эффекта Холла, мы получили, что насыщение магнитополевой зависимости дифференциального тока Холла в этой системе качественно коррелирует с обнаруженным ранее [6] в слабых магнетиках насыщением напряжения Холла с ростом магнитного поля. Этого следовало ожидать в силу соотношений (1) и (2). Вместе с тем из эксперимента следует, что дифференциальный метод тока Холла является более чувствительным для выявления АЭХ, чем холловское напряжение. Таким образом, развитый в настоящей работе подход к изучению роли токов намагничения оказывается более прямым и наглядным, чем применявшийся ранее прецизионный анализ полевой зависимости холловского сопротивления. Представленный в работе дифференциальный метод тока Холла также может найти практическое применение для получения информации о степени неоднородности образцов.
Работа выполнена в рамках государственного задания ФАНО России (тема «Электрон» Г.р. № АААА-А18-118020190098-5) и при частичной поддержке гранта РФФИ (№ 18-32-00198 мол_а).

