Дискуссия о том, какова судьба делокализованных состояний, ответственных за переходы между различными плато квантового эффекта Холла, при уменьшении магнитного поля mB = wCt<<1, имеет длинную историю [1–3] и остается в центре внимания в свете того, что микроскопическая теория квантового эффекта Холла (КЭХ) до сих пор не построена [4] (wC = eB/m*, nc, m*, t = l/VF, l и m концентрация, эффективная масса, время свободного пробега, длина свободного пробега и подвижность носителей заряда соответственно). Главный вопрос – происходит ли исчезновение (всплывание) делокализованных состояний в ходе квантового фазового перехода или объясняется кроссовером от слабой локализации (квантовые интерференционные эффекты в слабом магнитном поле) к сильной локализации в режиме КЭХ [5, 6]. Исторически теоретические представления основывались на глобальной фазовой диаграмме КЭХ [1], в которой существование делокализованных состояний в сильных магнитных полях может быть согласовано с отсутствием делокализованных состояний в нулевом магнитном поле, предсказываемым скейлинговской теорией локализации в 2D-случае [7], только если делокализованные состояния всплывают выше энергии Ферми, когда магнитное поле уменьшается до нуля (гипотеза «всплывания») [6].
В последние годы появились работы, рассматривающие проблему перехода в фазу КЭХ в решеточных моделях (network models). Так, используя суперсимметричный подход, в [2] модель сетки была переформулирована в терминах лесенки суперспинов, последующий анализ которой с учетом суперсимметричной нелинейной сигма-модели позволил подтвердить универсальность описания переходов в КЭХ как в области квантующих, так и классически слабых магнитных полей. В [5], используя слабо-киральную модель сетки для численного анализа предсказаний теории скейлинга относительно перехода от андерсоновского к квантово-холловскому изолятору, показано, что введение сильной локальной неоднородности подавляет интерференцию, и транспорт сводится к классической перколяции, соответствующей протеканию через две подрешетки, связанные друг с другом случайными связями. Получено скейлинговское соотношение, связывающее компоненты тензора магнетопроводимости σxy ~ σxxk, где значение критического индекса k различается в пределе сильной и слабой неоднородности. В [8] в численном исследовании с использованием модели Андерсона на квадратной решетке была показана возможность существования так называемой «антилевитации», когда по мере увеличения степени беспорядка W, либо увеличения напряженности магнитного поля B, энергии делокализованных состояний оказываются меньше энергий уровней Ландау, относящихся к идеальной системе, а для достаточно сильного беспорядка существует зависящее от беспорядка критическое магнитное поле Bc(W), ниже которого вообще отсутствуют делокализованные состояния. Экспериментально, наблюдалось как всплывание делокализованных состояний (ссылки в [4, 6]), так и антилевитация [9].
В работе [6] показано, что при рассмотрении систем конечных размеров при конечных температурах поведение квантового эффекта Холла (с n > 2) в области слабых магнитных полей хорошо описывается возникшей из теории фазовых переходов и теории ренорм-группы скейлинговой теорией КЭХ без использования экзотических гипотез типа гипотезы «всплывания». Большая длина локализации x в магнитном поле в 2D системах ограничивает наблюдаемость всплывающих делокализованных состояний экспоненциально малыми температурами и экспоненциально большими размерами системы. При достижимых температурах и размерах системы холловское сопротивление будет монотонно возрастающей функцией магнитного поля. Вблизи магнитных полей, wCt = 1 температурная зависимость диссипативного сопротивления изменяется от слабого роста в слабых магнитных полях до уменьшения в сильных магнитных полях. Таким образом, переход от диэлектрического поведения в нулевом магнитном поле к возникновению делокализованных состояний в режиме КЭХ происходит посредством кроссовера между слабой локализацией при wCt < 1 и сильной локализацией в квантующем магнитном поле.
Обычно границей, разделяющей области магнитных полей, где отсутствуют делокализованные состояния и где делокализованные состояния ответственны за появление переходов между квантованными плато КЭХ, служит так называемая температурно-независимая точка (Тind-точка) на кривых магнитосопротивления (МС), снятых при различных температурах. Скейлинговые свойства МС в Тind-точке в представлении, что в ней происходит квантовый фазовый переход из диэлектрического состояния в фазу КЭХ, изучены в ряде работ [10–12]. Однако, существует точка зрения, что природа Tind-точки связана с совместным действием классического циклотронного движения и квантовых интерференционных эффектов. Интерпретация экспериментальных данных (рис. 1) в рамках первой модели представлена в [12].
|
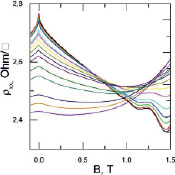
Рис. 1. Зависимости ρxx(B) при T = (1,8–20 К) |
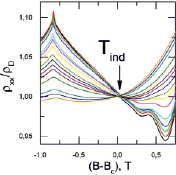
Рис. 2. Зависимость ρxx/ρD от (B-Bc) при T = (1,8–20 К) |
Цель исследования: анализ происхождения температурно-независимой точки в классически слабых магнитных полях на кривых ρxx(B, T) в модели параболического отрицательного магнетосопротивления в наноструктурах n-InGaAs/GaAs для получения новой информации о природе перехода из диэлектрической фазы в фазу квантового эффекта Холла.
Материалы и методы исследования
Рост образцов n-In0.2Ga0.8As/GaAs осуществлялся методом металлорганической газофазной эпитаксии на подложках GaAs в НИФТИ Нижегородского университета группой Б.Н. Звонкова. Будут обсуждены результаты, полученные на тех же образцах, что и в работах [12]. Структуры были симметрично легированы в барьерах Si (ND = 1018 cм-3), ширина спейсера Ls = 19 нм. Эффективная масса носителей заряда m* = 0,058m0, где m0 – масса свободного электрона.
Проведены измерения ρxx(B, T) и ρxy(B, T), в магнитном поле B до 2Тл и при температурах T = 0,05–20 K в структурах n-InGaAs/GaAs с одиночными квантовыми ямами. Эксперименты проведены в Центре коллективного пользования «Испытательный центр нанотехнологий и перспективных материалов» ИФМ УрО РАН на установках Oxford Instruments и Quantum Design.
Результаты исследования и их обсуждение
На рис. 1 показаны полученные из эксперимента зависимости ρxx(B, T) и ρxy(B, T) для образца с одиночной квантовой ямой. В слабых полях, B < 0,7 Тл, сопротивление образца показывает «диэлектрический» ход при изменении температуры: ρxx(B, T) увеличивается при уменьшении T. При достижении некоторого значения Bc отмечено обратное поведение, т.е. при повышении температуры ρxx(B, T) растет. Для структуры с одиночной квантовой ямой эта тенденция хорошо прослеживается при B > Bc вблизи магнитных полей, где ρxx(B, T) = ρxy(B, T). Температурно-независимая точка смещается в большие поля с повышением температуры. При B ≈ 0,9 Тл в образцах начинаются осцилляции Шубникова – де Газа (с фактором заполнения v = 8). Отрицательное магнитосопротивление, наблюдаемое в области магнитных полей B ≲ Bc, связано с квантовыми интерференционными поправками к проводимости.
При высоких температурах и в слабых магнитных полях, квантовые эффекты являются несущественными, и проводимость может быть рассчитана из кинетического уравнения (выражение Друде)
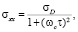(1)
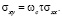
В отсутствии магнитного поля в слабонеупорядоченных 2D системах (kFl>>1) при низких температурах проводимость определяется проводимостью Друде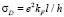 
и вкладами от квантовых интерференционных поправок двух типов 
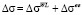(слабая локализация и электрон-электронное взаимодействие). В диффузионном режиме 
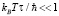и в магнитных полях 
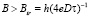(D – коэффициент диффузии), где подавлены эффекты слабой локализации, продольное МС дается выражением [13]
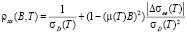. (2)
Видно, что rxx квадратичным образом зависит от B и при mB = 1 перестает зависеть от T (так называемая, модель параболического отрицательного МС).
На рис. 1 для образца InGaAs/GaAs с одиночной квантовой ямой в интервале T = (1,8–20 К) представлены экспериментальные зависимости rxx(B), на которых видна размытая по температуре Tind точка. В [14] было показано, что такое размытие связано с температурной зависимостью подвижности электронов m(T). В работе [12], где было изучено критическое поведение МС в области wCt@1, применен довольно грубый способ учета температурной зависимости m(T): измеренные значения ρxx(B, T) и ρxy(B, T) были инвертированы в тензор магнетопроводимости (1), а при обратном превращении серия кривых ρ*xx(B, T) при разных температурах была посчитана с учетом зависимости rxy(B, T = 1,8 K) только для одной температуры.
На рис. 2 приведены те же данные, что и на рис. 1, построенные в координатах [(B-Bc); rxx/rD], что позволяет аккуратно учесть зависимость m(T). В полном соответствии с выражением (2) прекрасно видна температурно-независимая точка, Tind. Полученные результаты позволяют сделать вывод, что природа температурно-независимой точки определяется совместным действием классического циклотронного движения и квантовых интерференционных эффектов слабой локализации и электрон-электронного взаимодействия.
Согласно выводам [6] квантовый фазовый переход из диэлектрической фазы в фазу КЭХ возможен только тогда, когда в режиме КЭХ наблюдается только плато с номером n = 1 (n = 1). В этом случае классическая проводимость (1) при переходе КЭХ-диэлектрическая фаза в слабых магнитных полях может быть порядка е2/2h и масштаб кроссовера x может быть микроскопическим. И тогда в Tind точке должно наблюдаться скейлинговое поведение [10].
Для иллюстрации условий, в которых в нашей системе происходит переход из диэлектрической фазы в фазу КЭХ, была построена фазовая диаграмма (рис. 3), представляющая собой аналог глобальной фазовой диаграммы КЭХ [1]. В зависимости от степени беспорядка в системе переход из диэлектрической фазы в фазу КЭХ может происходить как через промежуточные фазы квантовохолловской жидкости, соответствующие факторам заполнения n > 1, так и непосредственно в фазу с n = 1 [10]. Видно, что в нашей системе наблюдаются две хорошо выраженные фазы КЭХ с n = 2 и n = 1, а значит, согласно [6], мы должны иметь дело с кроссовером в Tind точке, что подтверждает наши выводы относительно ее происхождения.
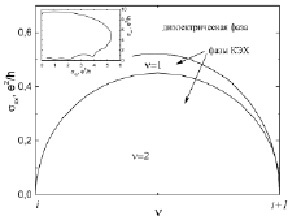
Рис. 3. Часть фазовой диаграммы КЭХ, согласно представлениям [3], структуры n-In0.2Ga0.8As/GaAs с одиночной квантовой ямой при Т = 0,05 К, полученная в магнитных полях до 16 Тл. Обрыв линии, разграничивающей диэлектрическую фазу и фазу КЭХ с v = 1, соответствует достижению предельных значений магнитных полей в экспериментальной установке. На вставке: зависимость σxx(σxy) при Т = 0,05 К
Хочется отдельно выделить, что наблюдаемые нами пиковые значения sxx = 0,45 e2/h для n = 2 и sxx = 0,52 e2/h n = 1 замечательно соответствуют предсказаниям теории (см., например, обзоры [7], что наблюдалось на эксперименте в единичных случаях (см. ссылки в работе [15]), что характеризует выбранную систему как идеальный модельный объект.
Выводы
Итак, экспериментально показано, что происхождение температурно-независимой точки на семействе кривых ρxx(B, T), находящейся при wCt@1, связано с совместным действием классического циклотронного движения и квантовых интерференционных эффектов слабой локализации и электрон-электронного взаимодействия, что может свидетельствовать в пользу того, что переход из диэлектрической фазы в фазу квантового эффекта Холла является кроссовером от слабой локализации (квантовые интерференционные эффекты в слабом магнитном поле) к сильной локализации в квантующих магнитных полях в режиме КЭХ.
Работа выполнена в рамках государственного задания по теме «Электрон» (Г.р. № АААА-А18-118020190098-5), при поддержке РФФИ: проекты № 18-02-00172 и № 18-02-00192; при частичной поддержке программы фундаментальных исследований УрО РАН, проект № 18-10-2-6.