Возможность решения задачи повышения работоспособности подшипников скольжения, при сохранении конструктивных параметров и заданных нагрузок, базируется на положении, что цапфа установлена в опорной обойме с гарантированным зазором и, следовательно, не соприкасается с обоймой по полной поверхности. Поэтому контактные напряжения будут определяться нагрузкой, приложенной к валу, деленной на фактическую площадь контакта. Применение износостойких покрытий, позволяющих получать рациональное сочетание высокой твердости поверхности и конструкционной прочности опоры в целом [1, 2] не в полной мере решают проблему. За счет зазора контакт вала с обоймой осуществляется только по части полной поверхности вала или втулки. Обеспечить беззазорное соединение технологическими методами механической обработки не представляется экономически нецелесообразным и является трудоемким, требующим применения пригоночных работ. В подобных случаях применяется метод регулирования. Для этого в обойму необходимо запрессовать промежуточное кольцо, которое затем перед началом эксплуатации подвергают принудительному деформированию радиально приложенными нагрузками. Точки приложения и величина нагрузки будут определяться обеспечением необходимого закона изменения зазора по дуге контакта и его минимального значения. Другим перспективным способом повышения износостойкости пары трения предлагается коррекция коаксиального положения вала с помощью применения постоянных линейных магнитов [3].
Для увеличения площади контакта необходимо уменьшить диаметр контактной поверхности обоймы на определенном угле дуги окружности до значений диаметра цапфы. При этом одновременно будут меняться зазоры и на остальной, свободной от контакта дуге сопряжения, а за счет этого будут меняться условия возникновения и поддержания заданных характеристик масляного клина. Очевидно, достижение требуемого результата зависит от выбора правильной схемы нагружения.
Цель работы: изучение различных схем деформирования промежуточного кольца радиальными нагрузками для увеличения площади фактического контакта в подшипнике скольжения и повышения его работоспособности.
Результаты исследования и их обсуждение
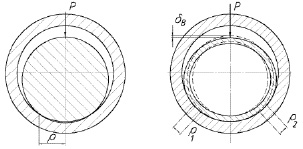
На рис. 1 представлены возможные схемы нагружения кольца радиальными силами.
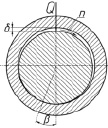
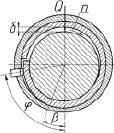
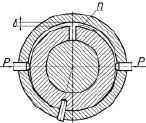
а) б) в)
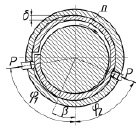
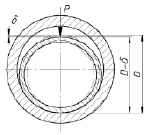
г) д)
Рис. 1. Изменение зазора между цапфой и кольцом в зависимости от полярного угла: а – стандартная схема нагружения; б – односторонняя схема нагружения; в, г – двухсторонние деформации разрезного кольца; д – деформация полой цапфы
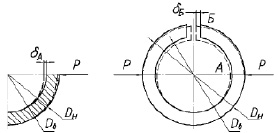
а) б)
Рис. 2. Схема нагружения: а – стержня по [4]; б – разрезного кольца
На схеме, представленной на рис. 1, а, показана стандартная схема нагружения вала в подшипнике. Вал установлен с зазором и под действием постоянной нагрузки занимает эксцентричное положение относительно оси отверстия обоймы. Максимальное сближение кольца с цапфой смещено на угол β. По обе стороны от точки наибольшего сближения вала с обоймой зазор принимает клиновидную форму. Вращаясь, вал увлекает за собой смазку, действуя как насос. Поступая в суживающийся по направлению вала зазор, масло, являющееся практически несжимаемой жидкостью, за счет сил давления приподнимет вал, одновременно сдвигая в направлении вращения. За точкой максимального сближения вала с обоймой расположена аналогичная расширяющая щель. За счет этого смазка приобретает ускоренное вытекание. Геометрические параметры этой щели определяет устойчивость и жесткость масляного клина. Когда в подшипнике цапфа установлена в обойме с гарантированным зазором, геометрические параметры входной и выходной щелей имеют конкретные значения. Возможно, что для большей устойчивости положения вала подшипника выходная щель должна быть не сужающейся, а равномерной по ширине, или даже сужающейся в направлении обратном вытеканию смазки, или иметь другую форму и размеры. Предельным положением поверхности кольца обоймы будет случай, когда под воздействием приложенной радиальной силы внутренний диаметр кольца примет значение радиуса цапфы. Деформация кольца может производиться по разным схемам. Каждая из схем отражает либо конструктивные особенности подшипника, либо преследует цель обеспечения заданного зазора и закона его изменения по углу охвата вала.
Первая из предложенных схем (рис. 1, б) позволяет обеспечить равенство радиусов вала и кольца на участке, обратном нагнетанию смазки в клиновидную щель. При отсутствии смазки, в неустановившиеся периоды, при пуске и остановке работы подшипника, когда наступает полусухое трение скольжения, вал будет полностью прилегать к поверхности кольца на угле φ, большем, чем при общепринятой схеме контакта.
За счет этого будут снижены напряжения в контакте, что приведет к уменьшению износа контактирующих поверхностей. В процессе установившегося процесса работы равномерная щель будет препятствовать быстрому вытеканию масла, что приведет к более устойчивой работе подшипника при изменяющемся температурном режиме.
Следующая схема (рис. 1, в) предназначена для обеспечения максимального угла охвата вала кольцом почти до полного совпадения контактирующих поверхностей. Эта схема предназначена для обеспечения минимальных напряжений в условиях сухого и полусухого трения. При жидкостном трении необходимо, чтобы вал приподнимался на некоторую величину. Охват кольцом вала в верхней части не позволит ему смещаться в этом направлении.
Схема (г) позволяет при решении тех же задач, что и схема (б), обеспечить изменение клинового зазора, в который увлекается масло. Схема (д) обеспечивает увеличение контактной поверхности за счет деформации полого вала. Последняя схема может быть использована, когда кольцо, по каким либо причинам, нецелесообразно выполнять разрезным. Наиболее оптимальный вариант, выбранный из представленных схем, может быть найден только после всестороннего исследования вопроса. Для этого необходимо определить геометрические параметры образующихся зазоров по длине угла охвата для разных схем нагружения кольца, характер течения смазки и ее подъемную силу.
Для того чтобы определить, какая из представленных схем является наиболее технологичной, необходимо провести теоретические и экспериментальные исследования данного вопроса.
В литературе [4, с. 99] рассмотрен вопрос деформирования стержня, выполненного в форме дуги круга, который закреплен на нижнем конце и изгибается силой Р, приложенной в радиальном направлении к верхнему концу (рис. 2, а).
Прогиб в точке приложения нагрузки (А) определяется формулой [4, 5]:
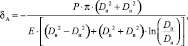 (1)
(1)
где P – нагрузка приложенная к цапфе; Dв, Dн – внутренний и наружный диаметры опорного кольца; Е – модуль упругости.
Для практических целей упрощенное решение формулы (1) дает выражение для определения силы, необходимой для деформации разрезного кольца цапфы на величину устранения зазора (δА):
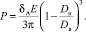 (2)
(2)
При этом разрезное кольцо должно иметь вырез, ширина которого должна быть не меньше, чем определяется выражением
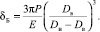 (3)
(3)
Другие варианты приложения сил достаточно подробно рассмотрены в литературе [6, с. 126], где приводятся схемы и формулы для расчета изменения диаметра колец. Например для схемы б (рис. 2) деформация точки А определяется выражением
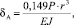 (4)
(4)
где r – радиус кривизны нейтрального слоя; J – момент инерции сечения кольца.
С учетом того, что сечение кольца прямоугольное, определяемое его диаметрами, а ширина b, получено выражение
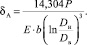 (5)
(5)
Или, для определения силы, необходимой для расчетной деформации:
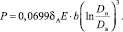 (6)
(6)
Для расчетного определения деформаций и сил в схеме (рис. 1, д) может использоваться зависимость из источника [6, с. 180]. Она дает зависимость деформации длинной цилиндрической оболочки от радиальной нагрузки, приложенной сосредоточенно на малой площади:
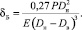 (7)
(7)
а) б)
Рис. 3. Схема сближения: а – при сплошном сечении цапфы; б – при применении цапфы в виде деформируемого кольца
Половина длины контакта по окружности, учитывая что это упругий контакт двух цилиндров с параллельными осями, определяется по формуле [7, с. 14] (рис. 3, а):
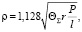 (8)
(8)
где l – длина контакта по ширине колец подшипника; ΘΣ = Θ1 + Θ2 – упругая постоянная для случая контакта двух деформируемых тел; r – главная кривизна в центре контакта:
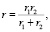
где r1 и r2 – радиусы цапфы и наружного кольца в точке контакта.
Тогда принимая во внимание, что кольцо деформируется и приобретает форму эллипса, контакт переходит в двухточечный (рис. 3, б) с полудлинами контакта ρ1 и ρ2, а фактическая площадь контакта увеличивается.
Заключение
Повышение работоспособности подшипников скольжения при сохранении конструктивных параметров и заданных нагрузок возможно путем увеличения фактической площади контакта между валом и обоймой за счет направленного деформирования обоймы по различным схемам. Математическое описание предлагаемых схем позволяет прогнозировать изменение контакта в подшипнике, а полученные математические зависимости пригодны для расчета геометрических параметров фактического контакта [8, 9] в подшипниках скольжения с предлагаемыми конструктивными решениями повышения несущей способности.

