Рассмотрим вопросы применения теории и методов математического моделирования к задачам повышения эффективности организации и управления государственной службы в Кыргызской Республике.
Данная работа состоит из двух частей. В первой рассматриваются вопросы количественного анализа и прогноза общей численности государственных служащих, и на этой основе разрабатывается вероятностная балансовая математическая модель в сфере госслужбы, а также строятся линейные и нелинейные прогнозные модели. Вторая часть исследования связана с разработкой информационной системы, которая нацелена на оптимизацию количественного состава государственной службы и соответствующей заработной платы государственных служащих, с применением соответствующих математических моделей. Таким образом, ставится задача оптимизации количественного кадрового состава государственной службы и выбора оптимальной заработной платы для повышения эффективности работы госслужащих.
Как известно, одним из основных разделов экономико-математического моделирования является построение балансовых моделей для экономических явлений, процессов и объектов. Эти модели основаны на хорошо известном методе баланса, то есть методе взаимного сравнения и сопоставления имеющихся материальных, трудовых и финансовых ресурсов и их потребностей [1]. При описании экономической системы в целом модель баланса относится к системе уравнений, каждое из которых выражает требование баланса между объемом продукции, производимой отдельными экономическими субъектами, и общим спросом на эту продукцию. Вместо понятия продукт введем более общее понятие – ресурс, и под балансовой моделью будем понимать систему уравнений, которая удовлетворяет требованиям соответствия между наличием определенного ресурса и его использованием.
Как мы знаем, балансовые модели строятся в виде числовых матриц, и в связи с этим их относят к тому типу моделей, которые называются матричными. В матричных моделях балансовый метод получает строгое математическое выражение. Несмотря на многообразие и специфику балансовых моделей, их объединяет не только общий формальный (матричный) принцип построения и единство системы расчетов, но и аналогичность ряда экономических характеристик. Рассмотрим наиболее распространенные задачи теории межотраслевого баланса (МОБ) и известные модели «затраты – выпуск» и применим их для задач количественного анализа и прогнозирования в сфере государственной службы [2].
Материалы и методы исследования
Если будем рассматривать государственную кадровую службу (далее ГКС) как отдельную систему, тогда можно применить теорию МОБ и построить балансовые модели, которые описывают состояние ГКС в стране.
Приведем сначала принципиальную схему МОБ (межотраслевой баланс) для ГКС и проведем следующие рассуждения и выкладки.
Пусть имеется n регионов (области и г. Бишкек) и количество государственных служащих (контингент ГКС). Пусть имеется m органов государственного управления и органов местного самоуправления (министерства, ведомства и их территориальные подразделения, областные и районные администрации, органы местного самоуправления (айыл окмоту, или сельские управы), можно добавить судебные органы, правоохранительные и т.д.). Пусть также задано количество уволенных из государственной службы или перешедших на другую работу. Тогда можно составить общереспубликанскую межведомственную и межрегиональную таблицу государственной службы (табл. 1).
Таблица 1
Межрегиональная и межведомственная таблица ГКС
|
Регион страны |
Кол-во служащих (министерства) |
Кол-во служащих (области) |
Кол-во служащих (районы) |
Кол-во служащих (айыл окмот) |
Кол-во уволенных служащих |
|
Бишкек Q1 |
q11 |
q12 |
q13 |
q14 |
P1 |
|
Чуйская область Q2 |
q21 |
q22 |
q23 |
q24 |
P2 |
|
Ошская область Q3 |
q31 |
q32 |
q33 |
q34 |
P3 |
|
Джалалабадская область Q4 |
q41 |
q42 |
q43 |
q44 |
P4 |
|
Иссыккульская область Q5 |
q51 |
q52 |
q53 |
q54 |
P5 |
|
Таласская область Q6 |
q61 |
q62 |
q63 |
q64 |
P6 |
|
Нарынская область Q7 |
q71 |
q72 |
q73 |
q74 |
P7 |
|
Баткенская область Q8 |
q81 |
q82 |
q83 |
q84 |
P8 |
В данной таблице в строках приведены семь областей и столица страны, в столбцах отражены министерства, ведомства и органы территориального и местного самоуправления. Понятно, что количество строк обусловлено существующим административно-территориальным делением. Понятно также, что количество столбцов балансовой таблицы можно варьировать в соответствии с имеющимися на сегодня органами государственного управления и существующим реестром государственных и муниципальных служащих.
Здесь приняты следующие обозначения: Q1, Q2 …Qn – численность государственных служащих по регионам; Р1, Р2, …Рn – количество уволенных госслужащих по регионам; q11 – численность госслужащих по региону 1 и министерству (ведомству) 1; q21 – численность госслужащих по региону 2 и министерству (ведомству) 1; в общем случае qij – численность госслужащих по i-му региону и j-му органу государственного управления. Для общего случая мы получим, следовательно n следующих уравнений:
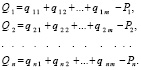 (1)
(1)
Назовем систему уравнений (1) системой балансовых уравнений контингента государственных служащих. Данные уравнения указывают на то, что общее количество госслужащих по региону равно сумме госслужащих по всем органам управления за минусом уволенных с госслужбы. Теперь в нашу модель введем следующие коэффициенты:
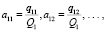
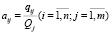 , (2)
, (2)
которые выражают отношение числа госслужащих каждого органа управления к числу госслужащих соответствующего региона, т.е. мы получим уровень или коэффициент государственных служащих. Таким образом, наши коэффициенты aij как показатели уровня госслужащих по каждому органу управления и по каждому региону образуют следующую матрицу:
 (3)
(3)
Используем теперь построенные соотношения (1), (2) и (3). Далее, применяя матричную форму записи
 (4)
(4)
и вводя следующие обозначения:
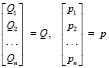 , (5)
, (5)
получим матричное уравнение следующего вида:
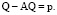 (6)
(6)
Тогда из последнего уравнения имеем
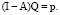 (7)
(7)
Проведем несложные преобразования, умножая на величину (I – A)–1 обе части уравнения (7), и окончательно получим
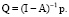 (8)
(8)
Здесь I – единичная матрица, Q и p – векторы-столбцы.
Перейдем к построению балансовой модели вероятностного или прогнозного типа с применением методов сглаживания динамических или временных рядов и регрессионного анализа. Для решения поставленной задачи воспользуемся необходимыми статистическими данными по динамике численности госслужащих за последние 25 лет. Сведем эти данные в виде нижеследующей табл. 2.
Таблица 2
Динамика численности государственных служащих
|
Годы |
Кол-во служащих (министерства) |
Кол-во служащих (области) |
Кол-во служащих (районы) |
Кол-во служащих (айыл окмот) |
Кол-во уволенных служащих |
|
1993 |
q11 |
q12 |
q13 |
q14 |
P1 |
|
1994 |
q21 |
q22 |
q23 |
q24 |
P2 |
|
1995 |
q31 |
q32 |
q33 |
q34 |
P3 |
|
… |
… |
… |
… |
… |
… |
|
2017 |
q251 |
q252 |
q253 |
q254 |
P25 |
По аналогии с табл. 1, здесь приняты следующие обозначения: q11 – численность госслужащих по региону 1 и министерству (ведомству) 1 по годам; q21 – численность госслужащих по региону 2 и министерству (ведомству) 1 по годам; в общем случае qij – численность госслужащих по i-му региону и j-му органу государственного управления по годам.
Приведенные данные позволяют перей- ти к прогнозным задачам, построению прогнозных моделей численности госслужащих с применением сглаживания временных рядов различными полиномами и разработкой линейных и нелинейных регрессионных моделей.
Анализ и сглаживание временных рядов
Располагая временными рядами по контингенту госслужащих, проанализируем путем сглаживания, как линейными, так и нелинейными методами. Далее получаем прогнозные модели, позволяющие создавать краткосрочные и среднесрочные прогнозы по численности госслужащих.
Основными моделями для анализа и прогноза динамических рядов будут выступать следующие полиномиальные уравнения:
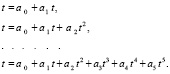 (9)
(9)
Здесь t – ряды численности государственных служащих, t – временной период, коэффициенты полинома ai – вычисляются в ходе анализа. При прогнозе временных рядов применяются 3-, 5-, 7-, 9-, 11-точечные схемы сглаживания. Программная реализация анализа и прогноза динамических рядов осуществлена на встроенном в операционную систему и офисный пакет языке VBA.
Далее рассмотрены основные регрессионные модели, которые построены с применением известного метода наименьших квадратов. Предложены следующие линейные и нелинейные модели для прогноза численности ГКС: линейная модель, параболическая модель, гиперболическая модель, степенная регрессионная модель, логарифмическая модель и модель показательной регрессии.
Как и для полиномиального сглаживания, осуществлена компьютерная реализация и составлены программы на языке VBA [3].
После анализа динамических рядов численности государственных служащих методами полиномиального сглаживания и регрессионного анализа переходим к исходным балансовым уравнениям и балансовой модели. Во всех соотношениях (1)–(8), касающихся балансовых моделей, входные данные представляют собой прогнозные значения, полученные по всем моделям (9). В результате получим вероятностные балансовые модели или прогнозные балансовые модели вида
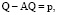
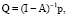 (10)
(10)
где все параметры нашей матричной модели представляют собой прогнозные значения на заданный период времени.
Построенные балансовые модели контингента государственных служащих дают следующие результаты.
Решение моделей (10) для Q позволяет получить решение следующим образом: во-первых, определить оптимальную и рациональную численность госслужащих по всем регионам и органам управления; во-вторых, решение моделей относительно p позволяет определить уровень текучести в госслужбе. Помимо этого, созданные модели и полученные решения позволяют разработать различные варианты количества государственных служащих по регионам и органам управления.
К достоинствам предложенных балансовых моделей, помимо простоты и эффективности, можно отнести следующее.
Во-первых, считая все параметры модели зависящими от времени t, получим линейные или нелинейные функции от времени, в результате переходим от стационарных моделей к динамическим линейным или нелинейным балансовым моделям.
Во-вторых, имеем простой переход к оптимизационным задачам. Для этого один из параметров балансовой модели вычленяем и выбираем в качестве целевой функции (например, потребуем минимума уволенных госслужащих, т.е. минимизации текучести кадров), в этом случае сама балансовая матрица выступает в качестве условия ограничения, и в результате получим известную оптимизационную модель целочисленного программирования.
Результаты исследования и их обсуждение
На основе разработанных математических моделей, а также новой иерархии в системе государственной службы КР проектируется и создается информационная система (рис. 1). Основное назначение данной системы заключается в оптимизации как количественного состава госслужащих, так и оптимизации заработной платы в сфере государственной службы на основе новой сетки и системы грейдов. Подробно система грейдов в сфере оплаты труда изложена в работе [4]. В известных работах академика Д.А. Новикова приводятся современные системы не только оплаты труда, но модели и методы стимулирования труда [5, 6].
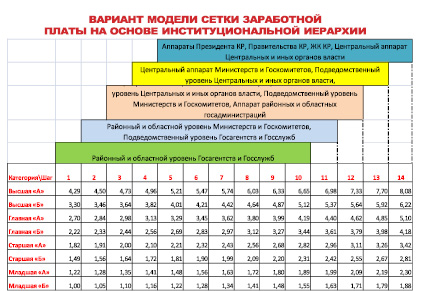
Рис. 1. Модель сетки заработной платы с многоуровневой иерархией
В нашей статье приведенные модели и информационная система опираются на современные системы оплаты труда. Как известно, создание эффективных систем стимулирования и оплаты труда является одной из центральных социально-экономических задач. Следует учитывать, что на уровень и принципы организации заработной платы государственных служащих влияют различные факторы. Отметим следующие факторы: производственные факторы, социальные факторы, рыночные факторы и институциональные факторы.
На сегодняшний день насчитывается большое число различных систем оплаты труда. Наиболее распространенные формы, модели и системы оплаты труда приведены в работе [7].
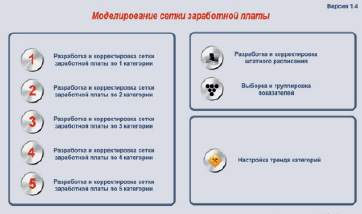
Рис. 2. Окно информационной системы (многоуровневая иерархия)
Предлагаемая информационная система включает в себя следующие основные блоки (рис. 2):
– блок «Разработка и корректировка штатного расписания», который позволяет создавать, формировать, редактировать и удалять штатные расписания любых органов государственного управления в Кыргызской Республике;
– блок «Выборка и группировка показателей» позволяет проводить численные эксперименты по количественным показателям органов государственного управления;
– блок «Настройка тренда категорий» позволяет проводить вычислительные эксперименты, математическое моделирование системы оплаты труда в сфере госслужбы КР.
Таким образом, осуществлена компьютерная реализация поставленных задач.
Заключение
В заключение отметим, что все поставленные в данной статье цели и задачи реализованы и решены. Предложены новые матричные модели для сферы государственной службы Кыргызстана. Составлены линейные и нелинейные прогнозные модели, которые можно также включать в матричные модели. Созданная информационная система позволяет проводить вычислительные эксперименты, численные расчеты и прогнозировать количественный состав государственных служащих. Спроектированная и разработанная автоматизированная информационная система была апробирована и прошла тестирование в Государственной службе КР.

