На ДВ России периодически проводятся учеты амурских тигров с целью оценки численности популяции [1, 2]. Они проводятся в зимнее время и могут охватывать различные территории, но методика является единой, и, соответственно, собираемая в ходе учетов информация тоже унифицирована. Во время учета на маршрутах собирается информация о следах амурского тигра. На основании этой информации производится оценка и приблизительный расчет количества особей, зафиксированных в ходе учета. До недавнего времени этот расчет производился только экспертным путем по методике с применением общих согласованных критериев, которые в свою очередь были разработаны и одобрены экспертами [3]. Поскольку данная методика задает только набор критериев, как по следовым параметрам оценивать принадлежность следов одной или разным особям, но не предлагает сам механизм действий, то каждый эксперт использует свой подход к решению этой задачи. Конечно, экспертная оценка может и, скорее всего, включает в процесс расчета другие и в том числе не формализуемые критерии, причем у каждого эксперта они могут быть свои. В результате один и тот же объем информации у разных экспертов дает разные результаты. Кроме того, при большом объеме информации точное следование критериям является крайне затруднительным ввиду чрезвычайной трудоемкости процесса.
Возникла необходимость создания автоматизированной системы расчета. Первый вариант алгоритма был реализован перед учетом 2005, и его общие принципы описаны в [3]. С тех пор алгоритм неоднократно модифицировался и тестировался, и здесь представлена его последняя версия.
Цель исследования: создание алгоритма расчета амурских тигров по результатам зимнего следового учета.
Материалы и методы исследования
Алгоритм основывается на методике, которая была разработана рядом экспертов в главе с Матюшкиным [3], и реализован на базе программных продуктов ArcGIS 10.3 и MS Access 2016 при помощи языков программирования Python (вер. 2.7) и VBA (вер. 7.0). В качестве исходных данных используется массив следов со следующими характеристиками: номер, промер передней пятки (при отсутствии этого показателя нужны промеры задней пятки или совмещенного следа), дата обнаружения, давность, отдельный параметр для выводков или особей, встреченных парами. Выходными данными является массив особей с принадлежащими им следами.
Результаты исследования и их обсуждение
Исходные данные – массив следов с заданными характеристиками. Следы в данном случае являются объектами, которые необходимо классифицировать. Для этого необходимо объединять определенные следы в группы, основываясь на критериях, которые допускают такое объединение, причем все возможные пары следов в пределах одной группы должны этим критериям соответствовать. Это задача классификации, где мы имеем четкий набор условий, из каких объектов может формироваться группа. Причем для оптимального решения задачи (а это задача формирования минимального количества групп) наши группы должны быть максимально полными. Для того, чтобы этого добиться, мы рассчитываем меры близости для каждой пары следов. В нашем случае для расчета такой меры используются два параметра: нормированная дистанция между следами и нормированная разница в промерах ширины пятки.
В общем, это некая численная мера вероятности того, что данная пара следов принадлежит к одной особи. Расчет данного показателя для следов ведется по формуле
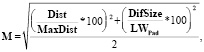
где M – искомая дистанция между следами в некотором пространстве, Dist – расстояние между следами (в км.), MaxDist – максимально возможная дистанция между следами для особи с предполагаемым полом и возрастом и с учетом разницы во времени, DifSize – разница в размерах передней пятки для данной пары следов, LWPad – лимитирующий параметр (допустимая разница в промерах пятки).
Показатель рассчитывается только для тех пар следов, которые по всем критериям могут быть отнесены к одной особи, и оперирует уже нормированными величинами. В результате мы получаем матрицу (M) метрик для всех допустимых пар объектов (в рамках заданных критериев). Слово метрика в данном случае подразумевает то, что мы переходим к понятию пространства и объектов в данном пространстве.
Далее мы приступаем к формированию групп. Для формирования максимально полной группы мы используем метод «ближайшего соседа» [4]. Берется начальный след и ищется ближайший к нему след. Затем для этих двух точек ищется ближайший к ним след, и так далее, пока мы не выберем все следы, удовлетворяющие заданным критериям. Первый след выбирается произвольно, и затем мы, таким образом, перебираем весь исходный массив следов. То есть мы пробуем все возможные варианты формирования группы. Таким образом, изначально у нас образуется количество групп, равное количеству следов в исходном массиве. Понятно, что это неоптимальное количество. Для начала мы избавляемся от абсолютно идентичных групп, т.е. от тех групп, следы которых полностью повторяются (у них отличается только порядок формирования группы). Затем мы фиксируем группы, в которых присутствуют уникальные следы, т.е. следы которые больше не встречались ни в одной из групп. Такие группы мы называем уникальными, и их мы уже не трогаем. Соответственно, у нас остаются те группы, следы которых, так или иначе, пересекаются с другими группами, в том числе и уникальными. Это и есть исходный массив для оптимизации. Это задача пересекающихся множеств, элементы которых не имеют однозначной идентификации. Нам же в конечном итоге надо оставить множества, которые имеют как минимум один уникальный элемент. Для проведения оптимизации необходимо выбрать какой-либо критерий, который бы рассчитывался для каждой группы, и оценивая который мы могли бы принимать решение о том, от каких групп нам следует избавляться и в какой последовательности это делать. В качестве такого критерия была выбрана мера избыточности группы. Эта мера рассчитывается как показатель того, насколько следы этой группы повторяемы в других группах. Причем она должна быть нормирована на размер группы. Рассчитывается она следующим образом.
Сначала мы рассчитываем коэффициенты уникальности/избыточности (US.t) для следов исходя из текущего набора групп. Данный коэффициент (далее US.t) для следа обозначает число групп, которые данный след содержат. Затем на базе рассчитанных коэффициентов US.t, мы рассчитываем коэффициенты уникальности/избыточности (далее US.c) для групп. Данный коэффициент US.c рассчитывается по формуле
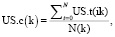
где US.t(ik) – коэффициент уникальности/избыточности для i-следа в k-группе, N(k) – кол-во следов в k-группе, i = 1,...N(k), k = 1,...K; где K – кол-во текущих групп.
Проще говоря, это усредненный по всей группе показатель коэффициента уникальности/избыточности (US.t) для следа. Когда он равен 1, то это значит, что все следы в группе уникальны, т.е. не повторяются больше ни в одной группе. Чем он больше, тем, значит, выше процент дублирования следов этой группы со следами в остальных группах. После расчета этой меры для каждой группы, можно рассчитать совокупную меру избыточности для всех анализируемых групп и начинать процесс отбрасывания лишних групп. Так как нам необходимо как можно дольше растянуть этот процесс (поскольку чем дольше будет идти этот процесс и больше будет итерационных шагов, тем меньше групп останется), то мы должны минимальным образом понижать совокупную избыточность анализируемых групп. Для этого на каждом итерационном шаге мы удаляем группу с минимальной избыточностью. Затем с учетом выбывшей группы пересчитываем все меры избыточности и повторяем так до тех пор, пока все группы не станут уникальными. Во время тестирования работы алгоритма пробовались также другие критерии и данный критерий показал наилучший результат. После этого, хотя требуемый минимум установлен, мы проводим процедуру удаления следов, имеющих неоднозначную идентификацию. В каждой группе существует как минимум один уникальный след и остальные неуникальные следы. Это множество следов, которые (в рамках построенной модели) имеют неоднозначную идентификацию (т.е. могут принадлежать разным особям) и являются предметом дальнейшего анализа. Нам необходимо провести безусловную идентификацию данных следов. Для этого в качестве критерия мы пользуемся мерой внутригрупповой дисперсии. Сначала по всем группам ищется неуникальный след, который вносит наибольший вклад в дисперсию группы. Данный след из этой группы исключается, и все показатели пересчитываются. Это процедура продолжается до тех пор, пока все следы во всех группах не станут уникальными. Вообще говоря, данная проблема довольно часто решается при решении задач классификации, и более универсальным и, видимо, более эффективным решением является выбор в качестве критерия оптимизации не просто дисперсии группы, а отношение внутригрупповых и межгрупповых дисперсий. Но поскольку такой подход более трудоемок (по времени и вычислительным ресурсам), а также могут быть проблемы со сходимостью, то этот вариант пока отброшен. Кроме того, основной задачей работы данного алгоритма является все-таки определение количества особей, а процесс безусловной идентификации следов при этом не так важен.
Основная модификация алгоритма заключалась во введении понятия «степень доверия к точности промера пятки» и его формализация для использования в алгоритме. Для этого был введен параметр «индивидуальная ошибка промера». Рассчитанная статистика по учетам показывает, что в целом для учета можно оценить, как варьируют показатели точности замера. И это позволяет в свою очередь внести те или иные поправки при корректировке следов конкретного учета. В исходной версии алгоритма при сравнении показателей промеров пятки мы использовали один параметр для оценки допустимого разброса. При этом предполагалось, что все следы имеют одну и ту же точность измерения. Но на самом деле это не так. Например, те следы для которых был осуществлен пересчет (с задней пятки или совмещенного следа) уже имеют большую ошибку. Следы с разной давностью также имеют разную ошибку измерения, след может увеличиваться в размерах со временем, и эта величина варьирует в зависимости от различных условий (количество солнечных дней в период между оставлением и обнаружением следа, температура, условия рельефа, глубина снега в месте замера и т.д.). Поэтому дополнительно для каждого следа определяется показатель «индивидуальная ошибка промера», параметры для расчета которого могут быть заданы в окне интерфейса (рис. 1) для конкретного рабочего массива.
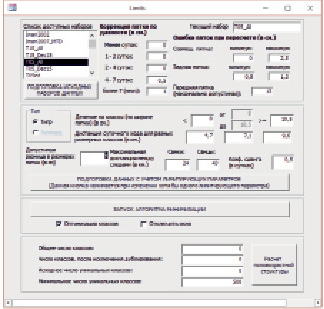
Рис. 1. Интерфейс программы расчета амурских тигров
В ареале амурского тигра на Сихотэ-Алине с 1997 г. работает программа мониторинга [5, 6]. В качестве примера работы алгоритма можно посмотреть мониторинговую площадку «Хор» за 2008 г.
В таблице можно увидеть рассчитанную для 9 следов диагональную матрицу метрик.
Матрица метрик для площадки Хор 2008
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
0 |
||||||||
|
2 |
35,8 |
0 |
|||||||
|
3 |
Х |
Х |
0 |
||||||
|
4 |
41,4 |
28,5 |
Х |
0 |
|||||
|
5 |
29,5 |
19,7 |
9,1 |
14,7 |
0 |
||||
|
6 |
Х |
Х |
Х |
Х |
Х |
0 |
|||
|
7 |
56,1 |
Х |
Х |
Х |
Х |
66,9 |
0 |
||
|
8 |
Х |
Х |
Х |
87,3 |
44,5 |
79,5 |
Х |
0 |
|
|
9 |
Х |
Х |
Х |
96,5 |
59,1 |
77,1 |
Х |
14,8 |
0 |
Визуально все объекты в этом пространстве удобно представить в виде графа (рис. 2), узлы которого – это точки следов, а ребра соединяют только те точки, которые можно отнести к одной особи с учетом заданных критериев. Цифры, расположенные на ребрах, означают меры близости в этой паре.
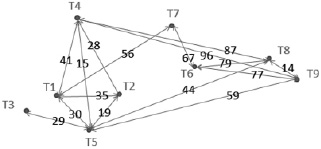
Рис. 2. Граф отношений между следами для площадки Хор 2008
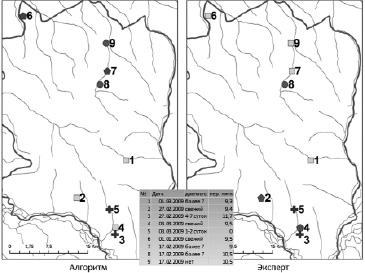
Рис. 3. Результат расчета по алгоритму и экспертная оценка ситуации на площадке Хор 2008
Окончательную картинку с результатами расчетов можно видеть на рис. 3. На ней значками одной конфигурации показаны следы отдельных особей. Номера на карте соответствуют номерам следов в таблице, где можно посмотреть наиболее важные параметры следов.
Как можно видеть на рис. 3, обе оценки дают одинаковое количество тигров – 4. Но распределение следов немного отличается между собой. При этом у эксперта (как можно видеть из таблицы следов) объединяются следы с разницей в более 1 см. Обработка большого количества мониторинговых площадок дает основания утверждать, что эта ситуация характерна для большинства экспертных оценок. То есть эксперты, как правило, не видят необходимости жестко соблюдать установленные критерии, для них это скорее руководство к действию, чем жесткая норма. При этом они могут руководствоваться своими внутренними соображениями, опытом, дополнительной информацией и так далее. Некоторые из этих дополнительных параметров тоже можно формализовать и ввести в алгоритм, что дает определенное поле деятельности для его модернизации. Также можно отметить, что в случаях, когда количество следов небольшое, то оценки численности экспертами и по алгоритму очень близки, но с увеличением количества следов оценки начинают сильнее отличаться [7]. Это, скорее всего, связано с тем, что большое количество следов экспертам сложнее обрабатывать и здесь срабатывает консервативный подход с тем, чтобы не насчитать лишнего, и, соответственно, критериями из методики пренебрегают еще больше. Алгоритму же не важно, какое количество информации он обрабатывает. Это зависит только от вычислительных ресурсов компьютера. Хотя лимит на общее количество обрабатываемых следов в алгоритме существует, и расчет может занимать несколько часов. По итогам работы алгоритма можно также получить сведения о половозрастной структуре исследуемой популяции.
Заключение
Надо отметить, что концептуально этот алгоритм не привязан только к амурскому тигру и следовым учетам. Его практическая реализация сделана для зимних следовых учетов амурского тигра и соответствующей методики, но в принципе, его можно использовать для следовых учетов других видов. Либо, в более широком смысле, для классификации объектов с рядом параметров, значения которых, при помощи определенных критериев, позволяют относить их к одному или разным классам.
Исследования проведены по заказу и при финансовой поддержке АНО-Центра «Амурский тигр».

