В современных науках существуют противоречия различных видов, так называемые парадоксы. Наличие парадокса в какой-либо теории свидетельствует о ее несовершенстве и побуждает исследователей вновь рассматривать все аспекты теоретического построения. Стремление разрешить парадокс и объяснить причины возникновения противоречия способствует совершенствованию научного знания.
Значительное число парадоксов до настоящего времени существует в аэрогидродинамике [1]. Исторически первым был обнаружен парадокс Даламбера – Эйлера, согласно которому при равномерном прямолинейном движении тела внутри несжимаемой и невязкой среды (жидкости или газа) рассчитанная сила сопротивления равна нулю. Этот парадокс проявляется и при стационарном безотрывном обтекании тела идеальной жидкостью (газом). В действительности тело всегда испытывает сопротивление движению со стороны окружающей его среды. Классическое объяснение возникновения парадокса Даламбера – Эйлера: реальные жидкости и газы обладают вязкостью, при движении тел в сплошной среде образуются вихри и поверхности разрыва скорости, то есть парадокс возник в силу переупрощенности модели [1]. Парадоксу Даламбера – Эйлера более 250 лет, но исследование причин его возникновения и условий существования продолжается [2–4].
Цель исследования: расчет давления потока разреженного газа, близкого по своим свойствам к идеальному, на элемент поверхности твердого тела. В работе рассматривается зависимость давления потока от следующих параметров: скорость потока, направление потока по отношению к поверхности, среднеквадратичная скорость теплового хаотического движения молекул газа в неподвижном объеме.
Метод и условия расчета
Действие газа на поверхность твердого тела является следствием множественных столкновений его молекул с поверхностью. Основное уравнение МКТ [5] позволяет рассчитать в рамках классической молекулярной физики давление молекул неподвижного (относительно некоторой поверхности) объема идеального газа на элемент этой поверхности. Движение молекул в газовом потоке отличается от движения молекул в неподвижном объеме газа тем, что кроме теплового хаотического движения молекулы участвуют в направленном перемещении потока в целом. В каждый момент времени тепловые скорости молекул, перемещающихся в направлении движения потока, превышают скорости молекул, направленные против потока. В результате этого перераспределения величин скоростей молекул (по сравнению с неподвижным объемом газа) и существует направленное движение потока.
В данной работе предлагается расчет давления газового потока на элемент поверхности твердого тела при следующих условиях и упрощениях:
1. Газ является идеальным, не имеет вязкости. Скорость потока невелика, плотность газа во всех его локальных объемах одинакова.
2. Столкновения молекул с поверхностью тела происходят абсолютно упруго, поверхность тела абсолютно гладкая, атомно-молекулярное строение тела не учитывается.
3. В системе отсчета, связанной с объемом газа, направления теплового хаотического движения молекул газа равновероятны, по величине скорости хаотического движения молекул одинаковы и равны некоторой скорости υо, усредненной по большому числу молекул.
4. В локальном объеме возле элемента поверхности газовый поток – плоский, безвихревой, стационарный.
Скорость молекулы газа в неподвижном объеме и в потоке
Рассмотрим неподвижные в системе отсчета XYZ элемент поверхности тела ΔS и прилегающий объем газа. Молекулы газа перемещаются хаотически, но часть молекул движется в направлении рассматриваемого элемента поверхности (рис. 1, а). За некоторое время Δt к элементу поверхности приблизятся молекулы, находящиеся в пределах полусферы с радиусом r = υо∆t, где υо – скорость молекул в тепловом движении.
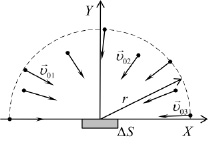
а) б)
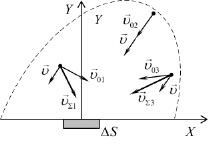
Рис. 1. Молекулы, движущиеся к элементу поверхности ∆S из неподвижного прилегающего объема газа (а) и газового потока (б)
В потоке газа молекулы двигаются и хаотически, и направленно (рис. 1, б). В этом случае поверхности ΔS за время Δt достигнут молекулы, движущиеся к ней из объема другой формы и размеров, так как вектор скорости каждой молекулы изменился в соответствии с вектором скорости направленного движения. Если поток газа движется со скоростью υ, то в некоторый момент времени вектор скорости каждой молекулы υƩi в соответствии с теоремой о сложении скоростей можно представить как геометрическую сумму вектора скорости этой молекулы в хаотическом движении υоi и скорости направленного движения υ.
На рис. 2 молекула газа находится в точке A. Элемент поверхности ∆S лежит в плоскости XOZ. Вектор суммарной скорости молекулы υƩi направлен к этому элементу. Скорость направленного движения потока газа υ находится на отрезке AD в плоскости, расположенной параллельно координатной плоскости XOY. Направление движения потока газа характеризуется величиной угла α (между вектором υ и перпендикуляром AB к плоскости, в которой лежит элемент поверхности). Угол β – угол между вектором скорости потока и вектором суммарной скорости молекулы υƩi. Углы θ и φ характеризуют направление суммарной скорости. В данной работе принято, что модули скоростей хаотического движения молекул в неподвижном объеме газа одинаковы и равны некоторой усредненной по всем молекулам величине υо, следовательно, суммарные скорости молекул, движущихся в одном направлении, также одинаковы υƩi = υƩ(θ, φ).
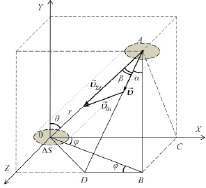
Рис. 2. Скорость молекулы газа в тепловом хаотическом движении – υоi, скорость направленного движения потока газа – υ, суммарная скорость молекулы – υƩi
Из геометрических соотношений (рис. 2):
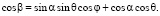 (1)
(1)
Суммарная скорость:
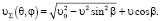
Если принять 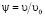 , то
, то
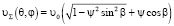 . (2)
. (2)
Число молекул, движущихся к элементу поверхности
В неподвижном объеме газа, в силу равновероятности движения молекул в любом направлении, векторы скоростей молекул будут равномерно распределены внутри полного телесного угла, равного 4π (соответствующего сфере). В пределах элемента телесного угла dω находится dN векторов скоростей. Плотность распределения скоростей молекул по направлениям в этом случае можно рассчитать как dN/dω = N/4π, где N – число молекул в рассматриваемом неподвижном объеме газа [5]. В газовом потоке плотность распределения скоростей молекул по направлениям зависит от скорости движения потока. Строгий анализ такого распределения требует отдельного исследования и выходит за рамки данной работы. При небольших скоростях потока можно принять, что плотность распределения скоростей молекул по направлениям не зависит от скорости направленного движения и равна N/4π.
Рассмотрим косой цилиндр, основание которого ΔS лежит в плоскости XOZ (рис. 2). Образующая цилиндра параллельна OA и равна r. В этом косом цилиндре молекулы двигаются в различных направлениях. Так как принято, что плотность распределения скоростей молекул по направлениям не зависит от скорости потока, то число частиц, движущихся к основанию цилиндра в потоке газа, можно считать равным числу частиц, движущихся к этому основанию из неподвижного объема [5]:
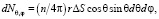
где n – концентрация молекул газа.
За время Δt основания цилиндра (рис. 2) достигнут молекулы, находящиеся на расстоянии 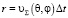 .
.
Таким образом, к элементу площади ΔS за время Δt в направлении, соответствующем углам θ и φ, приблизится следующее число молекул:
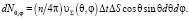 (3)
(3)
Давление потока газа на элемент поверхности
Изменение импульса молекулы массы m при абсолютно упругом столкновении с элементом поверхности (рис. 2): 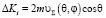 .
.
Изменение импульса для всех молекул из числа dNθ,φ (3) составит
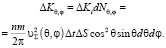
На элемент поверхности ΔS за время Δt воздействуют молекулы, движущиеся из различных точек всего прилегающего к поверхности объема. Всем возможным направлениям движения молекул к элементу соответствуют изменения угла θ от нуля до π/2, а угла φ – от нуля до 2π (рис. 2). Изменение импульса всех молекул, взаимодействующих с элементом ΔS за время Δt:
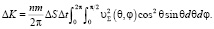 (4)
(4)
На основании изменения импульса (4) сила, действующая на элемент поверхности, рассчитывается как F = ∆K/∆t.
Давление на элемент поверхности:
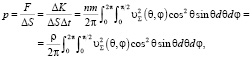 (5)
(5)
где m – масса молекулы, ρ = nm – плотность газа, υƩ(θ, φ) – суммарная скорость молекул, движущихся в направлении, которому соответствуют углы θ и φ (2).
Таким образом, давление потока идеального газа на элемент поверхности рассчитывается:
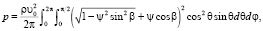 (6)
(6)
где угол β – угол между вектором скорости потока и вектором суммарной скорости молекул (рис. 2). Этот угол зависит как от направления движения молекул по отношению к поверхности (определяется углами θ и φ), так и от направления движения потока (угол α). Соотношение между тригонометрическими параметрами углов приведено в (1).
Статическое давление идеального газа – это давление молекул газа на элемент поверхности из неподвижного относительно поверхности прилегающего объема. Если прилегающий к поверхности объем перемещается относительно нее, то давление газа будет отличаться от статического. В зависимости от направления и величины скорости движения потока это давление может быть как больше, так и меньше статического. Давление потока идеального газа на элемент поверхности тела можно назвать кинетическим давлением. (Правильнее был бы термин «динамическое давление», но в последнем случае традиционно подразумевается кинетическая энергия направленного движения единицы объема газа или жидкости.)
Если υо – среднеквадратичная скорость хаотического движения молекул идеального газа в неподвижном его объеме, то статическое давление рассчитывается: po = ρυo2/3 [5]. Тогда отношение кинетического давления (5, 6) к статическому (относительное давление):
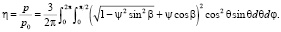 (7)
(7)
Относительное давление потока идеального газа η (7) рассчитано для различных по направлению и величине скоростей потока. Результаты расчета приведены на рис. 3. Если направленного движения газа нет, то отношение ψ (скорости потока к среднеквадратичной скорости молекул) равно нулю, а относительное давление потока (7) равно единице. Если поток направлен к поверхности и α = 0 (рис. 2), то относительное давление потока имеет максимальное (для данного отношения ψ) значение. В случае α = 180 ° (поток движется от поверхности) значение η минимально. Если скорость потока параллельна поверхности (α = 90 °), то увеличение скорости потока приводит к уменьшению его давления. Полученные результаты согласуются с широко известными экспериментальными данными.
Приведенный в данной работе метод расчета давления потока газа раскрывает механизм возникновения сил сопротивления при ламинарном обтекании тела, симметричного относительно его миделева сечения, даже в среде, лишенной вязкости. Для молекул, в данный момент времени движущихся к лобовой поверхности тела, геометрическая сумма их скоростей в тепловом хаотическом движении и вектора скорости направленного движения потока превышает усредненную тепловую скорость частиц. К кормовой стороне тела частицы двигаются (в среднем) со скоростью, которая меньше тепловой, так как движение к поверхности происходит за счет тепловой составляющей, а вектор скорости потока направлен «от поверхности». Таким образом, за одно и то же время к лобовой части тела приближается большее число частиц, нежели к кормовой части, и они оказывают в каждом столкновении большее силовое воздействие. Это различие числа и силы столкновений молекул газа с разными частями поверхности тела порождает разность давлений на лобовую и кормовую поверхности, то есть силу лобового сопротивления.
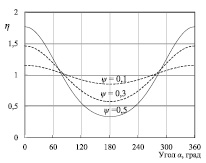
Рис. 3. Зависимость относительного давления потока (7) от угла α (между вектором скорости потока и нормалью к элементу поверхности) при различных относительных скоростях потока
Выводы
1. Метод расчета давления потока идеального газа на элемент поверхности тела, в соответствии с которым вектор скорости молекулы рассматривается как геометрическая сумма вектора тепловой скорости этой молекулы и вектора направленного движения потока, обеспечивает результаты в качественном отношении коррелирующие с экспериментальными данными для реальных газов.
2. Метод позволяет раскрыть механизм возникновения повышенного давления на лобовую поверхность обтекаемого тела (пониженного – на кормовую поверхность) в потоке газа, не обладающего вязкостью, и выявить одну из причин возникновения парадокса Даламбера – Эйлера: молекулы потока приближаются к лобовой части тела с большими (в среднем) скоростями, нежели к кормовой части. Классические аэродинамические модели рассматривают газ как сплошную среду и принимают во внимание только скорость ее направленного движения.
3. Положительными характеристиками предлагаемого метода расчета являются: обоснованность с позиций классической молекулярной физики, относительная простота, возможность использования в совокупности с известными расчетными комплексами [6, 7].

