Изучение физических свойств грунтов, которые определяют прочностные, деформационные, теплофизические, фильтрационные и другие их свойства, имеет особое практическое значение. Физические свойства грунтов определяются в процессе выполнения инженерно-геологических изысканий на площадках строительства всех видов сооружений, в том числе при строительстве подземных резервуаров [1]. В работе [2] излагается функциональная связь физических и прочностных характеристик грунтов, предназначенная для предварительной оценки и сопоставления искомых величин.
Грунты представляют собой многокомпонентные системы, состоящие из твердых минеральных частиц, воды в различных фазовых состояниях и газов. В работе [3] мерзлые грунты рассматриваются как многокомпонентные, многофазные физико-химические системы, изменяющиеся в зависимости от термодинамических параметров их состояния.
Показатели физических свойств грунтов взаимосвязаны друг с другом и изменение одного из них приводит к изменению других. В формулах взаимосвязи предшественников участвуют не все основные физические характеристики грунтов. В связи с этим предложена более общая формула, которая учитывает все основные показатели физических свойств грунтов.
В статье выполнен анализ формул взаимосвязи физических характеристик грунтов на всем диапазоне изменения их влажности от 0 до полной влагоемкости талых и мерзлых грунтов.
Результаты анализа формул взаимосвязи
Физические свойства грунтов характеризуются в основном плотностью грунта ρ, плотностью скелета грунта ρd, плотностью твердых частиц ρs, влажностью w, пористостью n, относительным содержанием воздуха (воздушной пористостью)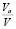 
и содержанием незамерзшей воды в мерзлых грунтах ww.
А.М. Пчелинцевым [4] получена следующая формула взаимосвязи физических характеристик грунтов:
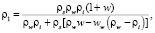(1)
где ρw – плотность воды; ρi – плотность льда.
Так как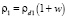 
, формулу (1) можно представить в виде
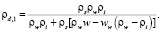(2)
В формуле (2) не учитывается количество воздуха, содержащегося в грунтах при неполном заполнении пор водой и льдом.
В связи со сложностью определения плотности мерзлых грунтов ненарушенного сложения в оттаявшем состоянии И.Н. Вотяковым [5] была предложена расчетная формула для определения плотности мерзлых грунтов по одной только влажности:
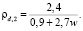(3)
Формула (3) получена при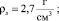 
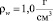и 
и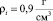з зависимости
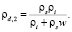(4)
В работе автора [6] предложена формула взаимосвязи, включающая все основные физические характеристики грунтов:
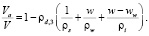(5)
Представим (5) в виде
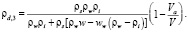(6)
Приведенные формулы взаимосвязи (2), (4) и (6) в зависимости от фазового состоянии воды в грунтах имеют вид
– в талых грунтах (ww = w)
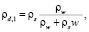(7)
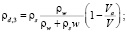(8)
– в мерзлых грунтах (ww = 0)
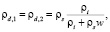(9)
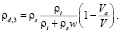(10)
При критических значениях влажности грунтов формулы (7)–(10) приобретают вид:
– в талых грунтах
при ww = w = 0
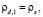(11)
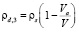(12)
или
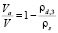= n; (13)
при ww = 0, w = wn,th и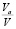 
= 0
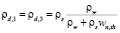; (14)
– в мерзлых грунтах
при ww = w = 0
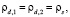(15)
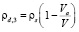(16)
или
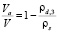= n; (17)
при ww = 0, w = wn,f и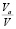 
= 0
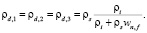(18)
Формулы (2) и (4) по сравнению с (6) дают, как следует из выражений (7)–(10), завышенные значения плотности грунтов, определяемые отношением
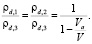(19)
На основании (13) максимальная погрешность по зависимости (19) при ww = w = 0 составляет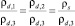 
.
Из зависимостей (11), (12) и (14)–(16) видно, что с увеличением влажности грунтов ошибка в определении плотности грунтов по формулам (2) и (4) уменьшается от максимальной при w = 0 до нулевого значения при w = wn. Ошибочность определения плотности грунтов по формулам (2) и (4) подтверждается равенствами (11) и (15), которые справедливы только для непористых грунтов.
Формула (6) позволяет определять по экспериментально найденным значениям ρd и w пористость, воздушную пористость и полную влагоемкость талых и мерзлых грунтов [6].
Эти определения можно сделать также из предварительно построенных графиков зависимости (5) [6]. Кроме того, при определенных допущениях формула (6) дает возможность определять количество незамерзшей воды в мерзлых грунтах [7].
Графическое представление зависимости (5) и определение количества незамерзшей воды в мерзлых грунтах
Зависимость (5) характеризует взаимосвязь показателей физических свойств грунтов, содержащих незамерзшую воду (0 ≤ ww < w). Графически эта зависимость может быть представлена [6] отдельно для талых грунтов и мерзлых грунтов в диапазоне незначительных фазовых переходов воды и можно пренебречь содержанием небольшого количества незамерзшей воды:
для талых грунтов (ww = w)
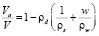, (20)
для мерзлых грунтов (ww = 0)
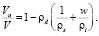(21)
Зависимости (20) и (21) являются линейными уравнениями. При w = 0 графики для талых и мерзлых грунтов сходятся в одной точке, ордината которой равна пористости грунта.
При полном заполнении пор грунта водой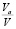 
= 0. Тогда из зависимостей (20) и (21) получаем выражения полной влагоемкости талых и мерзлых грунтов соответственно:
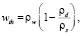(22)
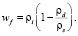(23)
В настоящее время разработаны различные методы определения количества незамерзшей воды в мерзлых грунтах, основанные на использовании теплового эффекта фазового перехода воды, адсорбции, криоскопии, ядерно-магнитного резонанса и др. [8, 9 и др.], требующие сложного оборудования и эксперимента, а некоторые из них имеют ограничения по температуре. Разработанный метод основан на положении о том, что количество незамерзшей воды в мерзлых грунтах практически не зависит от влажности грунта и закономерности деформации водонасыщенного образца грунта в условиях невозможности бокового его расширения при кристаллизации поровой воды [7]. Способ заключается в следующем. Образец талого грунта помещают в металлический стакан и насыщают водой до полного заполнения пор водой и замораживают при постоянной заданной температуре до полной стабилизации деформации, происходящей в условиях невозможности бокового расширения только в продольном направлении.
Из зависимости (5) при полном насыщении пор грунта водой, т.е. Va/V = 0 получаем выражение влажности грунта по незамерзшей воде
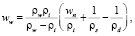(24)
где wn – влажность водонасыщенного грунта.
Влажность грунта при полной влагоемкости определяется зависимостью
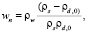(25)
где ρd,0 – плотность скелета грунта при w = wn.
Объем образца водонасыщенного грунта в процессе кристаллизации поровой воды увеличивается в соответствии с увеличением объема последней при переходе ее в лед и при невозможности бокового расширения образца зависимость (24) с учетом (25) принимает вид
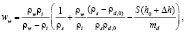(26)
где S – площадь поперечного сечения образца; h0 – начальная высота талого водонасыщенного образца грунта; Δh – приращение высоты образца в процессе кристаллизации поровой воды.
В зависимости (26) можно принять, что плотности компонентов мерзлого грунта при изменении температуры остаются неизменными, так как температурные деформации их очень незначительны. Тогда, предварительно определив значения плотности компонентов, массу и размеры образца, по экспериментально найденному значению приращения высоты образца при заданной температуре, можно определить влажность мерзлого грунта по незамерзшей воде.
Заключение
На основе анализа формул взаимосвязи показателей физических свойств грунтов установлено, что формула (6) по отношению к формулам (2) и (4) является более общей зависимостью, удовлетворяющей граничным условиям при критических значениях влажности грунтов, что позволяет по данным инженерно-геологических изысканий определять, кроме пористости и полной влагоемкости, воздушную пористость талых и мерзлых грунтов.
Формула (6) может быть представлена в виде графиков зависимости воздушной пористости талых и мерзлых грунтов от их влажности для оперативного определения ряда показателей их физических свойств
После определенных допущений из формулы (6) получена зависимость для определения количества незамерзшей воды по величине температурных деформаций образцов грунта.