В силу некоторой априорной информации о неизвестном точном решении поставленная задача классифицируется как некорректная задача [1, 2]. И поскольку класс задач, поставленных некорректно, зачастую требует регуляризующих алгоритмов для получения тех или иных решений, то поиск решения задачи сводится к нахождению решающей процедуры, качество которой охарактеризовано так называемой функцией риска, или средней величиной погрешности решения. Получение оптимальных решений [3] приближенными методами – процесс достаточно трудоемкий. Поиск оптимальных решений задач, поставленных некорректно, чаще всего оборачивается итерационным процессом [4], который в свою очередь должен быть обеспечен нахождением правила останова, что вызывает трудности и громоздкость при попытке оценить погрешности [5]. Подобные итерационные процессы и проблемы поиска оптимальных решений детально изучены в научных исследованиях известных ученых, таких как А.М. Федотов, а также в работах В.П. Тананы [6], А.Б. Бредихиной [7], А.П. Гогина [8], К.М. Чекирова [9], Е. Чжана [10]. В силу своей актуальности исследования по итерационным процессам и некорректным задачам, а также по методам регуляризации встречаются во многих других работах современных исследователей в области вычислительной математики. Основой для дальнейших рассуждений получения подобных оптимальных решений посредством итераций является изучение поведения исходных данных с аддитивными случайными погрешностями. Таким образом, получая ошибки в исходных данных, смоделированных случайными величинами и имеющих корреляционную взаимосвязь, имеем задачу, классифицируемую как некорректная задача и требующую нахождения решения методами регуляризации, в результате применения которых имеет место возникновение погрешности решения, или так называемой функции риска. В классе всех решающих процедур с указанной функцией риска требуется найти оптимальное решение, поиском и нахождением которого, и обусловлена актуальность и научная значимость данной работы.
Цель исследования: получение оптимального решения операторного уравнения первого рода в гильбертовом пространстве, посредством нахождения соответствующего вида оператора для множеств с регулярной границей. Наряду с этим построить оптимальный минимаксный алгоритм и задать способ построения регуляризующего алгоритма, а также параметра регуляризации для установки правила останова рассматриваемого итерационного процесса поиска решающей процедуры среди множества решающих процедур.
Материалы и методы исследования
В данной работе применены методы исследования операторных уравнений, операторы действуют в гильбертовых пространствах, исходные данные моделируются случайными величинами, то есть погрешности исходных данных заданы в соответствии с законами теории вероятностей и случайных величин. Использованы понятия нахождения решающей процедуры и функции риска, характеризующей качество решающей процедуры, итерационные методы нахождения оптимальных решений поставленной задачи посредством установки правила останова, а также модифицированный способ построения регуляризующего алгоритма получения оптимального решения и оценки их погрешностей.
Результаты исследования и их обсуждение
Пусть задан класс задач, описываемый в абстрактной форме операторным уравнением первого рода вида
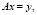(1)
где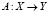 
– линейный оператор, действующий в гильбертовых пространствах X, Y, x – искомый, а y – данный элементы. Будем предполагать, что исходные данные заданы с аддитивной случайной погрешностью, т.е. вместо точного значения исходных данных y известно
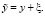(2)
Ошибки в задании исходных данных моделируются случайной величиной со значениями в пространстве Y с нулевым средним и заданным корреляционным оператором R, то есть
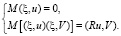
Для всех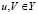 
здесь M – математическое ожидание, 
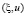– скалярное произведение в пространстве Y. Относительно неизвестного точного решения уравнения (1) задана априорная информация вида
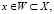(3)
где W – компактное, абсолютно-выпуклое подмножество пространства решений X. Если оператор уравнения (1) не имеет ограниченного, то рассматриваемая задача относится к классу некорректно поставленных [1].
Следуя [2], произвольное отображение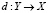 
будем называть решающей процедурой для задачи (1)–(3). Качество произвольной решающей процедуры будем характеризовать ее функцией риска 
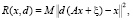то есть средней величиной погрешности решения при условии, что точное решения уравнения (1) равно x. Оптимальной решающей процедурой будем называть отображение d0, для которого справедливо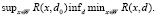 
В монографии [2] доказано, что при выполнении основного ограничения на задачу (1)–(3)
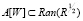. (4)
В классе всех решающих процедур с конечной функцией риска существует оптимальная, а в классе всех линейных решающих процедур построена последовательность линейных операторов, минимизирующая функционал погрешности вида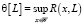 
.
Эта последовательность имеет вид
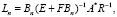(5)
где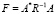 
– информационный оператор задачи, B – последовательность операторов конечного ранга, максимизирующих функцию.
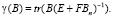(6)
На множестве T(W) – выпуклой оболочки семейства операторов единичного ранга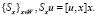 
Как отмечено в [2], выполнение условия (4) достаточно для того, чтобы информационный оператор задачи 
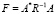является непрерывным.
В некоторых частных случаях задача о максимизации функции (6) решается аналитически, например когда множество W – эллипсоид или параллелепипед в пространстве X (см. раздел 14 в [2]). В случае параллелепипеда оператор B, максимизирующий функцию (6), суть оператор, этот параллелепипед порождающий. Ограничимся в целях простоты изложения априорным множеством, заданным в виде параллелепипеда. Для рассматриваемой в дальнейшем задачи итерационного уточнения, это довольно-таки общий случай, так как параллелепипед характеризует покоординатную точность априорного приближения к решению. Численная реализация задачи построения минимизирующей последовательности сопряжена с целым рядом сложностей, возникающих из-за необходимости обращать матрицы достаточно высокого порядка, к тому же при малом уровне шума являющиеся плохо обусловленными.
В настоящей работе сделана попытка обойти трудности, связанные с обращением матриц, при помощи итерационного процесса, дающего приближение к оптимальному решению с учетом того, что априорное множество W не слишком велико.
Будем считать, что нам из каких-либо предварительных вычислений известно приближение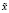 
к точному решению уравнения (1) и W – есть выпуклое центрально-симметричное множество с центром в 
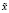(точность приближения 
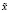). Наша задача состоит в построении итерационного уточнения приближения 
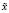. Не ограничивая общности 
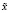, можно считать нулем пространства решения X.
Рассмотрим итерационный процесс вида
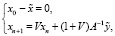(7)
где V – оператор перехода итерационного процесса (7). Например, для метода простой итерации, рассмотренного для задачи (1)–(3) в работе [9], оператор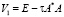 
, а процесс (7) превращается в
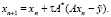(8)
То есть в легко реализуемую вычислительную процедуру. Из широко используемых на практике итерационных процессов приведем еще процесс с оператором перехода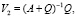 
для которого процесс (7) примет вид
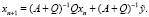(9)
Оператор Q выбирается из условий простоты обращения оператора A + Q. Итерационный процесс (9) порождает широко известное семейство регуляризованных, итерационных процессов.
В дальнейшем оператор перехода V будем выбирать из условия, что всегда определен оператор вида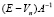 
.
Итерационный процесс (7) порождает семейство решающих процедур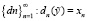 
. Функция риска решающей процедуры dn порождаемой процессом (7), примет вид
.
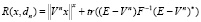Рассмотрим правило останова итерационного процесса (7). Будем выбирать оптимальное число итераций n0 из следующих условий
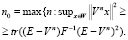(10)
При данном выборе числа итераций максимальная погрешность оптимальной итерационной процедуры допускает оценку
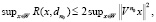(11)
которая для параллелепипедного множества корректности W согласно [2] примет вид
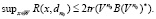(12)
В работе [7] было показано, что итерационный процесс (8) с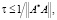 
если число итераций n0 выбирать по правилу останова (10), определяет состоятельную решающую процедуру, т.е. 
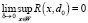, однако ее скорость сходимости для произвольного оператора Q будет меньше скорости сходимости оптимальной решающей процедуры (5).
Модифицируем теперь правило останова [9] так, чтобы итерационный процесс (7) определял оптимальную по порядку решающую процедуру, то есть имеющую ту же скорость сходимости к нулю при δ→0 что и оптимальная линейная решающая процедура [9]. Далее, приняв во внимание (12), правила прекращения решения для процесса поиска оптимального решения, запишем в виде
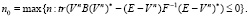(13)
Для простоты предположим, что оператор V – самосопряженный положительный и все операторы, входящие в представление (13), перестановочны. Определим следующее правило останова:
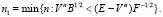(14)
Откуда следует, что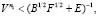 
следовательно
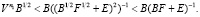
Таким образом,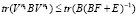 
, из правила (14) получаем
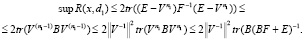
что гарантирует оптимальность по порядку итерационного процесса (7) с правилом останова (14). Очевидно, подобное правило останова можно определить и для неперестановочных операторов.
Следует отметить, что численная реализация итерационного процесса (7) значительно легче, чем реализация оптимальной линейной решающей процедуры, поскольку не требует обращений плохо обусловленных матриц, которые возникают при малых значениях мощности шума (мала величина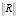 
). Само правило останова можно существенно упростить, рассматривая неравенства для норм Гильберта – Шмидта, входящих в итерационный процесс матриц.
Для практической реализации наиболее удобен процесс вида (9) с матрицей Q = B или Q = αE + B, если B вырождена, α ≥ 0. Этот процесс требует для достижения момента останова значительно меньше итераций, чем процесс вида (8).
Отметим также, что правило останова (10) пригодно и для произвольного множества корректности W.
Заключение
В данной работе построены линейные оптимальные, регуляризующие и итерационные алгоритмы для построения приближенных решений задач, описываемых линейным операторным уравнением, исходные данные которой представлены приближенными значениями. И на основе рассмотрения понятия класса решающих процедур для данного уравнения вводится понятие функции риска решающих процедур, порождаемых итерационными процессами. Методом модификации правила останова существующей процедуры установлено правило останова для исследуемого итерационного процесса, посредством чего находится оптимальное по порядку решение поставленной задачи. Стоит отметить, что подобные алгоритмы могут быть применимы и для других некорректно поставленных задач с перестановочными операторами. Особенностью рассмотренных методов поиска приближенного решения является то, что вместе с получением решения мы также получаем и оценку его погрешности.
Данный итерационный процесс построен в попытке избежать сложностей при аналитических решениях задач подобного рода.