Явление тепловой самодефокусировки излучения («тепловая линза») впервые было обнаружено и исследовано в лазерных резонаторах. Оно ограничивает предельную мощность оптоволоконных усилителей [1] и влияет на распространение света в оптических волноводных структурах [2, 3]. Мощность излучения внутри резонатора в несколько раз (а иногда и на порядки) превышает выходную мощность лазерного пучка. Поглощение света приводит к нагреву среды. Из-за этого показатель преломления изменяется Δn = (∂n/∂T)·ΔT.
Цель данной работы: изучить возможность применения метода «тепловой линзы» для определения показателей поглощения слабопоглощающих жидкостей. В жидкости образуется осесимметричное распределение показателя преломления вследствие явления теплопроводности и неоднородного нагрева. Практически всегда показатель преломления уменьшается с ростом температуры (∂n/∂T < 0). Поэтому по краям он будет больше, чем в центре пучка. Такое распределение показателя преломления эквивалентно рассеивающей линзе. В случае лазерного резонатора данный эффект вреден (увеличивается расходимость пучка, падает стабильность лазера, появляются паразитные моды), и с ним борются, например, используя жидкости для активной среды с меньшей температурной зависимостью.
Для определения показателя поглощения удобнее размещать исследуемое вещество вне резонатора [4]. Схема установки приведена на рисунке. Пучок света, генерируемый лазером 1, проходит через модулятор 2 (необходим, чтобы создаваемая тепловая линза меняла свое фокусное расстояние) и фокусируется собирающей линзой 3 в кювету с исследуемой жидкостью 4. Из-за дефокусировки в жидкости размер пучка в дальней зоне увеличится. Для того, чтобы найти относительное значение интенсивности на оси пучка использованы диафрагма 5 и фотодетектор 6. Вольтметр 7 может измерять переменное или постоянное напряжение и позволил померить относительное изменение светового потока.
Фокусное расстояние тепловой линзы
Показатель преломления среды зависит только от радиальной составляющей и может быть представлен как
n(r) = n(0) + r(∂n/∂r) r = 0 + (1/2)r2(∂2n/∂r2) r = 0 + ... (1)
В данном случае второе слагаемое обращается в ноль. Пренебрегая членами третьего и выше порядков и используя уравнение лучей [3]
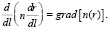(2)
Получим выражение, связывающее радиус кривизны луча с распределением показателя преломления:
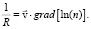(3)
Если при прохождении через кювету диаметр лазерного пучка меняется незначительно, то (3) принимает вид
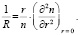(4)
Эффективное фокусное расстояние определяется длиной среды L и радиусом кривизны луча R:
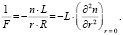(5)
Учитывая зависимость показателя преломления жидкости от температуры среды, получим
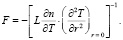(6)
Распределение температуры в среде
Запишем уравнение теплового баланса для изменения температуры ΔT в цилиндрических координатах:
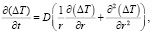(7)
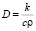, k – коэффициент теплопроводности, c – удельная теплоемкость, ρ – плотность вещества. Значения k, c, ρ, D для некоторых часто используемых жидкостей приведены в табл. 1.
Решение (7) приведено в [6] и имеет вид
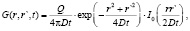(8)
Q – теплота, выделяющаяся на единицу длины. В данном эксперименте мы применяли непрерывный лазер, поэтому для получения конечного результата нужно проинтегрировать (8) по времени.
Схема экспериментальной установки: 1 – лазер, 2 – модулятор, 3 – собирающая линза, 4 – кювета с исследуемой жидкостью, 5 – диафрагма, 6 – фотодетектор, 7 – цифровой вольтметр
Таблица 1
Плотность, удельная теплоемкость, коэффициент теплопроводности и коэффициент температуропроводности для некоторых жидкостей [5]
|
Параметр |
Вещество |
Дистиллированная вода |
Ацетон (ЧДА) |
Этиловый спирт |
Изопропиловый спирт |
|
плотность вещества (•103), кг/м3 |
1 |
0,8 |
0,8 |
0,79 |
|
|
удельная теплоемкость кДж/(кг•К) |
4,18 |
2,22 |
2,41 |
2,08 |
|
|
коэффициент теплопроводности (•103), Вт/(м•К) |
588 |
160 |
166 |
154 |
|
|
коэффициент температуропроводности (•10-3), м2/с |
141 |
90 |
83 |
94 |
|
Был выбран одномодовый лазер с гауссовым профилем распределения интенсивности по сечению пучка:
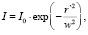(9)
w – радиус пучка, I0 – интенсивность излучения на оси пучка, I0 = P/(π•w2), P – мощность излучения.
Из (8) и (9) получим
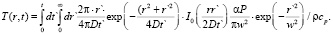(10)
В случае если z <<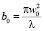 
, размер пучка при прохождении жидкости будет меняться слабо, и в первом приближении может быть принят постоянным.
Дважды дифференцируя по r и интегрируя (10) по r`, получаем
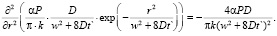(11)
Далее проинтегрируем (11) по времени импульса:
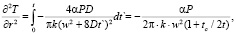(12)
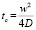– характерное время релаксации при тепловыделении.
Используя (6), получаем
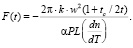
Если время велико –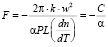 
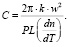(13)
Изменение диаметра пучка в дальней зоне
Рассмотрим пучок с гауссовым распределением интенсивности по сечению. Его размер на экране w (расстояние до экрана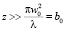 
) вычисляется как
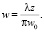(14)
При прохождении через диафрагму радиусом а останется мощность:
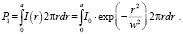
Так как
,
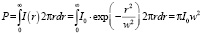то
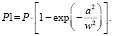
Если диафрагма мала, то прошедшая мощность
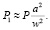(15)
Линза с фокусным расстоянием F изменяет радиус сферической волны по формуле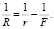 
Используя формализм комплексного параметра пучка q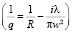 
, получим
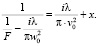(16)
Здесь х – расстояние до новой перетяжки, v0 – ее размер. Решив (16), найдем
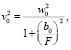
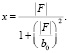(17)
Если показатель поглощения мал, то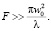 
Тогда
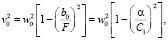
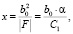C1 = C/b0. (18)
Найдем параметры пучка и мощность, прошедшую через диафрагму:
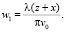(19)
Так как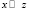 
, то
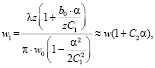(20)
α – показатель поглощения среды.
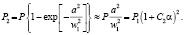(21)
В первом приближении:
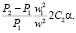(22)
Измерение показателей поглощения
В качестве источника излучения в установке, изображенной на рисунке, был использован полупроводниковый лазер OMEGA LASER PEN RP50 с длиной волны 650 нм и мощностью около 50 мВт. К сожалению, качество его излучения оказалось не очень высоким – не удалось реализовать предельно малый размер перетяжки. Характерный размер составил w0 = 100–150 мкм. Поэтому предельная чувствительность установки составила около 0,01 м-1. На точность измерений оказывало некоторое влияние и определение поглощения калибровочной жидкости. Для калибровки в исследуемую жидкость добавлялся раствор бриллиантовой зелени. По ослаблению пучка определялся показатель поглощения получившегося раствора α ~ 1 м-1. Для получения градуировочного раствора добавлялась в нужной пропорции чистая жидкость. По сравнению относительного изменения мощности после диафрагмы для исследуемой и для градуировочного раствора определялся искомый показатель поглощения. Результаты измерений приведены в табл. 2.
Анализ полученных данных позволяет сделать вывод о хорошем соответствии результатов опыта и ранее измерений по ранее известным методикам для не очень малых значений показателя поглощения жидкости.
Таблица 2
Сравнение показателей поглощения, измеренных методом тепловой линзы и найденных в литературных источниках (* – оценка по действительной части показателя преломления из дисперсионных соотношений Крамерса – Кронига [5])
|
Показатель поглощения α (м-1), (λ = 0,65 мкм) |
Дистиллированная вода |
Ацетон (ЧДА) |
Этиловый спирт |
Изопропиловый спирт |
|
Измеренный |
0,5 |
0,4 |
1,4 |
0,5 |
|
По литературным данным |
0,33–0,41 |
0,35 |
0,7 |
0,3* |
Заключение
Метод «тепловой линзы» может быть использован для определения показателя поглощения слабопоглощающих жидкостей. Для работы необходима предварительная калибровка установки на образцах с известным показателем поглощения. Главным достоинством метода является очень высокая чувствительность (до 10-4 м-1). К недостаткам следует отнести малый динамический диапазон ( < 100) при неизменяемой мощности лазера. Также ограничивает использование метода сложность перестройки по длине волны. Для нахождения спектра поглощения следует использовать лазеры на красителях, работающие в сине-зеленом или желто-красном диапазонах (как альтернатива для дискретных значений – аргон-ионный (криптонный) лазер с селекцией длин волн).