Голография Френеля с точки зрения математики – это преобразования Френеля, которые обычно сводятся к двумерным преобразованиям. С точки зрения физики происходит преобразование координат точек одного плоского объекта к координатам другого плоского объекта [1–2]. При расчете распределений световых полей мы имеем дело с трехмерной задачей, которая, в общем случае, описывается интегралом Кирхгофа. Решение такой проблемы даже с использованием численных методов, не говоря уже об аналитическом подходе, задача очень сложная. Поэтому для случая зоны Френеля используют так называемое параксиальное приближение, в котором предполагается, что размеры рассматриваемых объектов значительно меньше расстояний между ними. В этом случае трехмерная задача сводится к двумерной, для которой можно использовать аппарат преобразования Френеля.
Задача оценки амплитудных и фазовых распределений волны света, который отражается объемным объектом произвольного вида на заданную плоскость фиксации, является трехмерной, и решение ее представляет собой расчет трехмерных интегралов [3–5]. Расчет подобных интегралов – задача в вычислительном отношении очень сложная. Однако существуют естественные ограничения, которые дают возможность рассматривать трехмерный объект как двумерный. Поверхность объекта разбивается на элементы, каждый из которых можно приблизительно рассматривать как плоскость, а фазовые и амплитудные распределения по поверхности объекта замещаются распределением фаз и амплитуд на плоскости близкой к объекту.
При решении задач, целью которых является формирование изображений, важно уметь правильно передать распределение яркости и относительно крупные шероховатости объекта (т.е. отклонения от гладкости, значения которых сильно превышают длины волн освещающего источника) [6–8]. Указанные проблемы решаются определением распределения модуля отражающего коэффициента вдоль поверхности объекта, который при этом пересчитывается на плоскость, касающуюся объекта и расположенную нормально к линии рассматривания. Также необходимо задать геометрическую форму поверхности, используя которую можно сформировать распределение расстояний от каждой точки поверхности объекта до плоскости касания вдоль линии наблюдения [9–11].
Объемная голография Френеля с использованием двух опорных волн
На рис. 1 представлена схема записи голограмм на основе бесщелевого метода [12–13]. Схема является обобщенной, так как позволяет записывать по бесщелевому методу как отражающие, так и пропускающие объекты. На рис. 1 показано, что прошедшая сквозь объект или отраженная от него волна представляется, в соответствии с методом Габора, как сумма дифрагированной и недифрагированной составляющих.
Волны V1 и V2 освещают соответственно пропускающий и отражающий объекты.
Предложенная схема представляет собой совокупность двух схем записи голограмм: осевой метод Габора и внеосевой метод записи [14].
Рассмотрим подробнее метод Габора. В соответствии с этим методом пропускающий коэффициент прозрачного объекта σ(x, y) и волну U(x, y), которая проходит сквозь такой объект, можно рассматривать как одновременное действие двух волн:
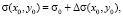 (1)
(1)
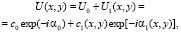 (2)
(2)
здесь σ0 и ∆σ соответственно описывают недифрагированную и дифрагированную составляющие коэффициента пропускания; c0 – амплитуда недифрагированной составляющей волны (когерентный фон), соответствующая σ0; c1(x, y) – амплитуда дифрагированной составляющей волны, соответствующая диффузной компоненте ∆σ(x0, y0); α0 и α1(x, y) – фазы этих волн.
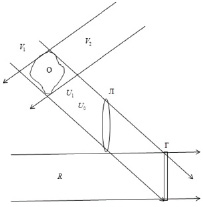
Рис. 1. Запись голограмм пропускающих и отражающих объектов
Для записи голограммы используются три волны: 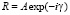 – опорная волна;
– опорная волна; 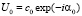 – невозмущенный фон (волна) (действует так же как и опорная волна, но соосная предметной);
– невозмущенный фон (волна) (действует так же как и опорная волна, но соосная предметной); 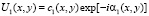 – объектная волна. Здесь A, U0, U1 – амплитуды, γ, α0, α1 – фазы этих волн. Г – регистрирующая среда (голограмма), Л – изображающая линза, О – исследуемый объект. Для условия «тени»
– объектная волна. Здесь A, U0, U1 – амплитуды, γ, α0, α1 – фазы этих волн. Г – регистрирующая среда (голограмма), Л – изображающая линза, О – исследуемый объект. Для условия «тени»
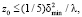 (3)
(3)
здесь z0 – удаление объекта от плоскости голограммы, δmin – размер наименьшей неоднородности объекта, l – длина световой волны. Расчет распределения интенсивности световой волны рядом с голограммой
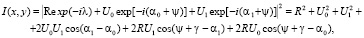 (4)
(4)
где 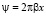 ,
, 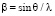 – частота в пространственной области, l – длина световой волны, R2 и
– частота в пространственной области, l – длина световой волны, R2 и 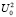 – энергетические характеристики опорного поля и невозмущенной компоненты объектного поля,
– энергетические характеристики опорного поля и невозмущенной компоненты объектного поля, 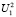 – световой оттиск записываемого объекта [15].
– световой оттиск записываемого объекта [15].
Введем новые переменные для описания распределения интенсивности световой волны I(x, y) рядом с плоскостью голограммы в следующем виде:
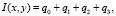 (5)
(5)
где
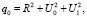
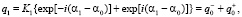
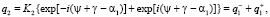
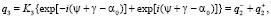
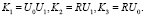 (6)
(6)
Подобная голограмма записывается в среде, осуществляющей фазовую модуляцию (например, галоидосеребряные фотографические слои и др.). Соответствующая обработка фотопластинки в линейном режиме приводит к тому, что пропускание такой голограммы можно выразить посредством экспоненциальных функций, т.е. пропускание является нелинейной функцией по отношению к интенсивности I(x, y) и его можно представить в виде произведения трех экспоненциальных сомножителей
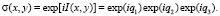 (7)
(7)
Как было сказано ранее, если такую голограмму осветить волной, которая совпадает с исходной опорной волной R(k), то за голограммой формируются три световых пучка, соответствующие 0 и ±1 порядкам дифракции (рис. 2).
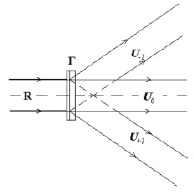
Рис. 2. Восстановление голограммы
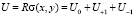 . (8)
. (8)
Представим выражения для интенсивностей волны в 0 и ±1 порядках дифракции после голограммы в следующем виде:
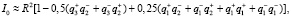 (9)
(9)
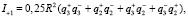 (10)
(10)
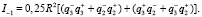 (11)
(11)
Если голограмму освещать когерентным светом, то в выражениях 9–11 каждая из компонент имеет следующий смысл: 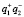 и
и 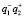 – показывают, что в нулевом порядке присутствуют два изображения – действительное и мнимое;
– показывают, что в нулевом порядке присутствуют два изображения – действительное и мнимое; 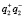 и
и 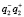 – в +1 порядке присутствует действительное изображение, а в –1 порядке – мнимое изображение;
– в +1 порядке присутствует действительное изображение, а в –1 порядке – мнимое изображение; 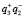 и
и 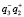 – проекции действительных и мнимых изображений во всех трех порядках дифракции;
– проекции действительных и мнимых изображений во всех трех порядках дифракции; 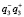 – невозмущенный фон. Также в (9) присутствуют слагаемые
– невозмущенный фон. Также в (9) присутствуют слагаемые 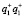 и
и 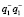 , которые описывают искаженные действительное и мнимое изображения, фазовые множители которых удвоены. При использовании белого света для восстановления, вышерассмотренные компоненты описывают:
, которые описывают искаженные действительное и мнимое изображения, фазовые множители которых удвоены. При использовании белого света для восстановления, вышерассмотренные компоненты описывают: 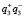 – световой спектр, возникающий из-за действия голографической решетки;
– световой спектр, возникающий из-за действия голографической решетки; 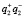 – изображения объекта в действительной и мнимой областях, имеющие радужную окраску;
– изображения объекта в действительной и мнимой областях, имеющие радужную окраску; 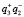 и
и 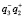 – сфокусированные изображения исходного объекта.
– сфокусированные изображения исходного объекта.
Выводы
Предложена многолучевая модель записи голограмм Френеля для объемных объектов. С этой целью разработан способ перехода от трехмерного объекта к двумерному. В основе метода лежат принципы геометрической оптики, позволяющие произвести пересчет характеристик трехмерного объекта на плоскость, расположенную как можно ближе к объекту. Таким образом трехмерная задача расчета световых полей вблизи плоскости голограммы сводится к двумерной, что позволяет воспользоваться преобразованиями Френеля при расчетах.
Показано, что световая волна от объекта может быть рассмотрена как сумма двух волн: волна не испытавшая возмущений, а значит, ее можно использовать как опорную волну, и возмущенная объектом волна, которая несет информацию об объекте. Волна от объекта – это классическая объектная волна, а невозмущенная составляющая действует как вторая опорная волна, соосная объектной волне, помимо основной, падающей под углом к объектной волне. Такой подход позволяет рассматривать записанную голограмму как сочетание двух голограмм – осевой (голограмма Габора) и внеосевой (голограмма Лейта).
Учет невозмущенной составляющей объектной волны при записи голограмм приводит к возникновению дополнительных компонентов, описывающих новые функциональные свойства рассмотренной голограммы.

