Задача изучения сложных фазовых объектов, особенно динамического типа, чаще всего сводится к необходимости сбора данных об изменениях оптической неоднородности во времени в этих средах. Более того, если мы говорим об интерферометрических исследованиях, это должна быть довольно подробная интерферометрическая база данных, то есть запись интерферограмм объекта или среды, снятых в разные последовательные моменты времени и при разных значениях чувствительности интерферометра [1–3]. Чтобы более точно судить о временных изменениях, происходящих в исследуемой фазовой среде, необходимо делать похожие снимки с довольно короткими временными интервалами [4]. Однако при обработке всей этой информации, особенно если необходимо сравнить интерферограммы исследуемой фазовой среды, полученные в разные моменты времени, приходится иметь дело с огромным количеством данных [5–7]. При вводе данных в компьютер необходимо использовать методы, позволяющие значительно уменьшить их общий объем [8]. В этом случае способ должен позволить не потерять важную часть информации во время сокращения, а также реализовать способность восстанавливать весь первоначальный объем информации, переносимой интерферограммами. В качестве такого метода предлагается использовать расфокусировку. Аберрация типа расфокусировки позволяет исключить высокочастотный компонент из интерферограммы, максимально упростить его, то есть, в конечном итоге, значительно уменьшить объем информации, вводимой в компьютер. Однако в случае обработки изображений, таких как интерферограммы, то есть имеющих сложную структуру, довольно сложно идентифицировать определяющие характерные точки. Построение сложных стилизованных изображений из простейших «информативных фрагментов» [9], которые являются наиболее характерными особенностями данного изображения, является вариантом решения проблемы, рассмотренной выше. Расфокусировка изображений оптическими методами позволяет выделить эти «информативные фрагменты», которые в дальнейшем распознаются голографическим коррелятором. С выхода голографического коррелятора информация поступает на компьютер. Компьютер синтезирует исходное изображение с использованием информативных фрагментов [10–11]. Теоретически и экспериментально было показано, что дефокусировка сопровождается выделением информативных элементов с инверсией контраста только в оптических системах, использующих некогерентное освещение. Степень расфокусировки подбирается в каждом случае индивидуально, в зависимости от характеристик высокочастотной составляющей сложной интерференционной картины. При некогерентном освещении оптического устройства, используемого вместе с голографическим коррелятором, возможна реализация нужного значения расфокусированности изображения.
Целью данного исследования является разработка математической модели некогерентной оптической системы, которая позволила бы осуществить предварительную, низкочастотную фильтрацию сложных интерферограмм в системах их автоматической обработки и дешифровки.
Функция передачи оптического устройства, реализующего степень расфокусированности исследуемого изображения
Образование изображения с заданным значением расфокусированности происходит при прохождении некогерентного излучения сквозь оптическое устройство, включенное в схему коррелятора. Схема такого оптического устройства, сквозь которое проходит некогерентное излучение, показана на рис. 1.
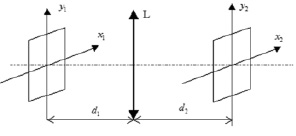
Рис. 1. Схема расфокусирующего оптического устройства: d1 и d2 – расстояния от объекта до линзы, и от линзы до изображения соответственно. L – линза
Условие использования некогерентного светового излучения предполагает, что оптическое устройство нелинейно по отношению к интенсивности излучения. В этом случае преобразование световой интенсивности можно записать в следующем виде, т.е. как преобразование свертки [12]:
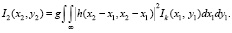(1)
Здесь Ik аппроксимация геометрической оптики для интенсивности идеального изображения; h – импульсная характеристика, то есть амплитуда в плоскости изображения для точки, имеющей координаты (x2, y2), когда она подвергается воздействию точечного источника, который расположен в точке (x1, y1); g – действительная константа; I2 – интенсивность изображения в точке с координатами (x2, y2).
Как показывает частотный анализ этих оптических систем, в них реализовано линейное преобразование для значений интенсивности светового поля. Учитывая этот факт, можно ввести частотные спектры распределения значений Ik и I2, которые нормированы относительно идеального спектра, и значения которых задаются соотношениями [13]:
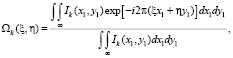(2)
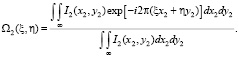(3)
Здесь ξ, η значения координат в области частот. Аналогично функция передачи оптического устройства может быть нормализована:
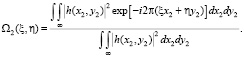(4)
Если мы применим теорему о свертке к выражению (1), то получим соотношение:
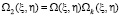. (5)
Функция Ω(ξ, η) является передаточной функцией оптической системы. Ω(ξ, η) – фактически это весовой коэффициент сложного типа для частотной переменной в точке (ξ, η), который вводится оптической системой и который присваивается весовому коэффициенту переменной, имеющей нулевую частоту. Для известной оптической когерентной передаточной функции системы G(ξ, η) можно рассчитать оптическую передаточную функцию, используя следующую формулу:
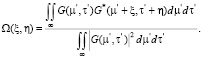(6)
Здесь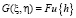 
изображение Фурье функции отклика.
После изменения переменных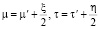 
у нас получается выражение:
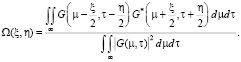(7)
В случае когерентной системы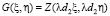 
[14]. Здесь Z(x, y) функция отверстия; λ – усредненное значение длины волны; d2 – это удаление объектива от изображения.
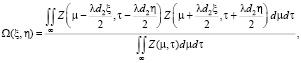(8)
здесь вместо функции Z2 подставляем Z. Принимаем во внимание, что Z имеет значения 1 или, вне изображения, 0.
Рассмотрим оптическую систему при наличии аберрации. Если мы рассмотрим погрешности фазы в точке с координатами (x, y) на выходе оптического устройства как kV(x, y), где k – характеристика волны, и установим погрешность оптической длины пути V, то передающий коэффициент можно записать в виде:
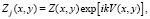(9)
Zj(x, y) – запись функции зрачка в общем виде. Если мы рассмотрим аберрацию, то для когерентной передаточной функции мы можем написать соотношение:
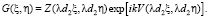(10)
Пересечение функци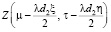й 
и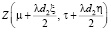 
может быть представлено в виде некоторого соотношения B(ξ, η).
Присутствие аберраций изменяет выражение для оптической передаточной функции:
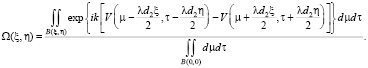(11)
При условии, что мы рассматриваем дефокусировку как аберрацию, известная формула тонкой линзы преобразуется в следующий вид:
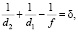
здесь d1 – расстояние между объектом и объективом; d2 – расстояние между объективом и плоскостью сфокусированного изображения; f – фокусное расстояние объектива; δ является характеристикой смещения плоскости, в которой мы видим изображение, по отношению к плоскости, в которой изображение будет сфокусировано. Выражение для эффективной ошибки длины пути с такой аберрацией, как дефокусировка, можно записать как [15]:
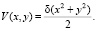
Результаты моделирования процесса дефокусировки
На рис. 2 показаны результаты расфокусировки интерферограмм для фазового объекта, такого как тонкая линза, которые были получены соответственно в каналах 3 и 4 голографического интерферо- метра [1–3]. На всех фигурах внутренний квадрат представляет интерференционную картину в присутствии фазовой среды. За пределами внутреннего квадрата мы имеем интерференционную картину, которая получается в отсутствие фазовой среды, при этом все остальные параметры интерферограммы остаются неизменными [4]. Представленные на рисунках интерферограммы имеют различные значения расфокусирующего коэффициента (расфокусирующие коэффициенты интерферограмм на рис. 2, a–в равны δ = 0; 0,003; 0,007). Рисунки показывают, что правильный подбор расфокусирующего коэффициента интерферограммы позволяет довольно четко различить муаровую структуру, то есть низкочастотную составляющую. В этом случае дефокусировка работает как пространственный фильтр, который удаляет высокие частоты в интерферограммах, которые создаются на выходе голографического интерферометра с несколькими выходными каналами.
а) б) в)
Рис. 2. Интерферограммы линзы. Канал 3 голографического интерферометра с несколькими выходными каналами [1]: а) расфокусировка отсутствует; параметр расфокусирирующий коэффициент δ = 0; б) расфокусирирующий коэффициент δ = 0,003; в) расфокусирирующий коэффициент δ = 0,007
Выводы
Разработана математическая модель, описывающая процесс расфокусировки изображений для случая некогерентной оптической системы и немонохроматического света.
Предложенная модель может быть использована в качестве метода предварительной подготовки изображений (интерферограмм) в компьютерных системах для обработки сложных интерферограмм без использования устройств оптической расфокусировки. Метод расфокусировки может быть достаточно эффективно использован в двух случаях:
а) в качестве фильтра нижних частот, который при соответствующем выборе параметра расфокусировки уменьшает влияние высокочастотных компонентов сложной интерференционной картины и более четко различает муаровую картину.
б) как способ выделения информативных фрагментов изображений, с помощью которого можно при необходимости синтезировать исходное изображение. Этот метод предварительной обработки изображений позволяет существенно сократить объем входных данных при их компьютерной обработке, классификации и декодировании интерферограмм.