Процесс ортогонализации позволяет построить ортонормированный базис Ψ как для евклидова, так и для сепарабельного гильбертова пространства на основе исходного базиса Ф того же пространства. Реально базис строится для евклидова пространства. В случае гильбертова пространства приходится проводить усечение счетного базиса, а при недостаточной точности вычислений наращивать удерживаемый отрезок базиса. В любом варианте отрезок исходного базиса будем обозначать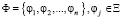 
, где Ξ – пространство, в котором выполняется ортогонализация в соответствии со скалярным произведением (φ1, φ2).
Цель исследования: обоснование выбора метода эффективной ортогонализации базисов евклидова/гильбертова пространств.
Классическая ортогонализация Грама-Шмидта
Результатом перекрестных скалярных произведений элементов строится матрица Грама
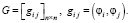(1)
Процесс построения матрицы Грама является наиболее энергоемким во всех энергетических методах вычислений, в которых требуется проводить ортогонализацию. Он опирается на теорему Шмидта [1]. Она конструктивна: процесс доказательства одновременно является эффективным алгоритмом ортогонализации.
Теорема Шмидта
Пусть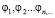 
– линейно независимая система элементов в евклидовом пространстве Ξ. Тогда в Ξ существует система элементов 
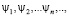удовлетворяющая условиям:
1) она ортонормированная: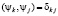 
(δkj – символ Кронекера);
2) каждый элемент ψn есть линейная комбинация элементов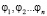 
:
;
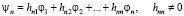3) каждый элемент φn представим в виде
.
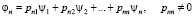Каждый элемент системы 1)–3) определен однозначно с точностью до множителя ±1.
Доказательство и алгоритм ортогонализации являются рекурсией.
Шаг 1. Элемент ψ1 определим так: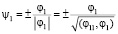 
.
Отсюда видно, что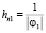 
.
Шаг k. В n-мерном векторном пространстве оцениваются «проекции» элемента ψk на уже построенные ортонормированные «направления», соответствующие всем предыдущим ψj, благодаря чему оценивается остаток bk (не равный нулю из-за линейной независимости векторов ψj базиса)
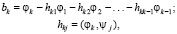
после чего делением на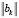 
, 
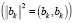выполняется нормирование нового ортогонального элемента: 
.
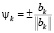Отметим важную особенность процесса ортогонализации Шмидта: на k-ом шаге используется новый независимый элемент φk исходного базиса, через него и построенные ранее элементы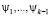 
строится ортонормированный элемент ψk. Можно существенно поднять эффективность процесса ортогонализации, переписав его в форме, удобной для машинного счета, использующей лишь перекрестные скалярные произведения элементов исходного базиса, которые сведены в матрицу Грама (1). Рассмотрим некоторые подходы.
Матричный алгоритм Шмидта
Классический алгоритм Шмидта предполагает вычисление скалярных произведений на каждом шаге процесса ортогонализации. Алгоритмически более удобным представляется предварительное вычисление матрицы Грама. После этого ставится вопрос о разложении ее на матричные множители, позволяющие явно выражать элементы ортонормированного базиса через элементы исходного базиса:
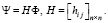(2)
Детальное рассмотрение классической процедуры ортогонализации позволяет описать алгоритм, в котором используется матричная форма представления промежуточной информации. Для удобства интерпретации нижеизложенного введем специальные матричные обозначения, сопутствующие вычислительному процессу. В частности, для краткости будем обозначать конструкциями вида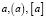 
скаляр, вектор-столбец и матрицу соответственно. Условимся для этих объектов единичной размерности использовать упрощенную запись 
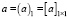, чтобы не возникало иллюзии, что в результате матричных операций появляется скаляр.
Полагаем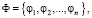 
Ψ= =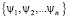 
вектор-столбцами. Введем матричное обозначение для скалярного произведения (векторов, квадратных матриц) в виде
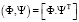, (3)
так что результатом свертки (3) является n×n-матрица. Такая запись удобна тем, что позволяет расшифровывать процедуру перемножения векторов или матриц из элементов пространства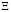 
через матричную операцию. Например, матрица Грама есть скалярное произведение вектор-столбцов Ф
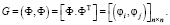
Очевидны свойства однородности операции при работе со скалярными числовыми множителями α, β, векторами a, b из чисел, n×n-матрицами A, B:
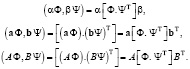(4)
Свойства (4) устанавливают цель построения матрицы Шмидта H, выражающей ортонормированный базис Ψ через исходный Ф (2). Поскольку скалярное произведение ортонормированного вектора Ψ на себя должно давать единичную матрицу Е:
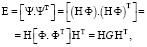
то разложение Шмидта состоит в представлении матрицы Грама в форме
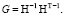(5)
Рекурсивный матричный алгоритм
Его суть состоит в последовательном наполнении матрицы Шмидта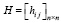 
и ей сопутствующей матрицы 
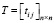посредством приращения строк. Обозначим 
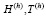верхнетреугольные квадратные матрицы (подматрицы H, T соответственно) размерностью k×k. Изначально обе матрицы полагаем обнуленными: 
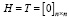. Через 
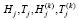обозначаем j-е строки соответствующих матриц.
Шаг k = 1. Полагаем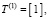 
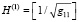. Далее – по индукции.
Шаг k. Перебираем строки матриц в последовательности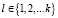 
и назначаем значения матрицы T(k) по правилу
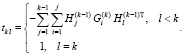
Оцениваем норму остатка разложения по уже построенному отрезку базиса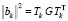 
и нормируем коэффициенты строки к матрицы Шмидта
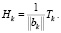
При достижении k предела n процесс построения матрицы Шмидта окончен. Погрешность вычисления можно оценить вычислением любой матричной нормы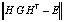 
или использовать ресурсы, предусмотренные конкретной вычислительной системой (например, в Mathematica [2] для такой цели можно использовать оператор Accuracy).
Метод Холецкого
Разложение Холецкого построено для класса эрмитовых матриц, для которых транспонирование в сочетании с комплексным сопряжением возвращает исходную матрицу. Матрица Грама относится к более узкому классу симметричных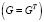 
, состоящих из действительных чисел.
Ассоциация с разложением Холецкого [3]
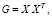(6)
которое для любой положительно определенной матрицы G существует и единственно [4], устанавливает связь матрицы Шмидта и нижнетреугольной матрицы Холецкого
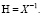(7)
Прямой алгоритм разложения таков.
Квадратная n×n-матрица изначально полагается равной нулю: X = 0.
1. Перебирается последовательность строк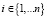 
.
2. Для каждого i перебираются номера столбцов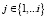 
.
Вычисляется частичная сумма
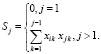
Значение элемента xij матрицы X равно
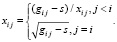
Нижнетреугольная матрица X построена. Точность разложения можно оценить нормой невязки разложения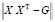 
.
Замечание. В силу симметрии матриц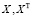 
последовательность действий можно организовать не по столбцам, а по строкам (реализовано в Mathematica процедурой CholeskyDecomposition).
Способ сингулярного разложения
В силу эрмитовости неотрицательно определенная матрица имеет сингулярное разложение [3]. Положительно определенная симметричная матрица Грама, как частный случай эрмитовой, может быть представлена в спектральной форме:
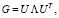(8)
где Λ – диагональная матрица спектра, состоящая из положительных собственных чисел G, т.е.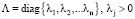 
. При этом спектр Λ может быть упорядочен в любой последовательности с учетом кратности (например, в порядке невозрастания значений λj). Унитарная (в случае матрицы Грама – ортогональная) матрица U удовлетворяет условию
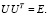
Представим Λ в виде произведения двух функций от матрицы, обозначенных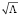 
и состоящих из соответствующих корней из положительных собственных чисел: 
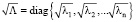. Тогда
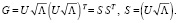(9)
Здесь матрица H не является нижнетреугольной матрицей Холецкого. Тем не менее подстановка
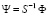
ортогонализирует исходный базис Ф пространства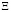 
.
Замечание. В системе Mathematica сингулярное разложение реализуется операцией SingularValueDecomposition. При этом собственные числа матрицы упорядочиваются по убыванию.
Сравнительный анализ эффективности алгоритмов декомпозиции
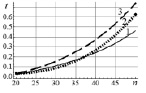
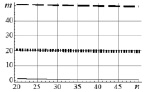
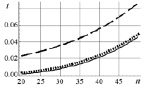
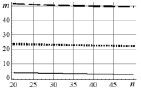
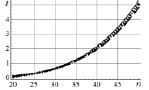
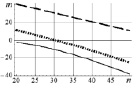
Проведен сравнительный анализ эффективности методов разложения (сингулярного (С), Холецкого (Х), Шмидта (Ш)) в зависимости от размерности n (ось абсцисс) матрицы Грама при различных значениях мантисс μ действительных величин, участвующих в разложениях, в их десятичном представлении. Графически обработанные результаты численного эксперимента сведены в таблице, где метками 1, 2, 3 обозначены значения μ = 10, 30, 60 соответственно. В левом столбце таблицы по оси ординат отложено время счета (секунды), в правом – гарантированное количество m доверительных разрядов после запятой в десятичном представлении результатов счета. Кривые построены на основе обработки статистической информации методом наименьших квадратов. Для сбора статистики для каждой размерности n генерировалась случайным образом система линейно независимых векторов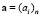 
количеством N >> 1 раз (практически принималось N = 20) и строились матрицы Грама посредством скалярного произведения 
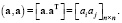Затем выполнялись действия в соответствии с анализируемым методом и оцениваемые характеристики статистически усреднялись и аппроксимировались полиномами четвертой степени от размерности n и резервируемой длины мантиссы представления десятичных чисел m. Результаты представлены сериями кривых таблицы при 
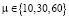. Анализ результатов позволяет сделать ряд выводов.
Зависимости от размерности матрицы Грама
|
Быстродействие |
Точность |
|
|
С |
|
|
|
Х |
|
|
|
Ш |
|
|
Выводы относительно времени счета t':
1) t' в методе Шмидта значительно превышает таковое в методах сингулярного разложения и разложения Холецкого и длина мантиссы на нем практически не сказывается;
2) t' в сингулярном разложении существенно зависит от размерности базиса; при базисах малой размерности длина мантиссы практического значения не имеет; при любом m t' значительно превышает время счета по Холецкому;
3) в отношении t' метод Холецкого является по сравнению с использованными средствами наиболее ресурсосберегающим; при коротких мантиссах t' практически одинаково для различных n, однако для мантисс существенного размера начинает значительно увеличиваться.
Выводы относительно точности, оцениваемой количеством A доверительных знаков после десятичной точки:
1) в методах Холецкого и сингулярного разложения точность разложения слабо зависит от размерности n; при малой длине мантиссы она может теряться;
2) точность метода Шмидта существенно падает с ростом n; при малых размерностях n довольно быстро теряется: переход графиков через нулевую отметку свидетельствует о явной непригодности результатов решения к использованию; достичь доверия результатам можно только за счет существенного увеличения рабочего диапазона мантиссы чисел в десятичном представлении.
Замечание. Ортогонализация базиса является энергозатратным процессом в решении механических задач энергетическими методами, например, методом граничных состояний. Методом граничных состояний решались задачи для различных сред: упругих, анизотропных [5, 6], термостатики, термоупругости [7].
Выводы
1. Выигрышным во всех отношениях является метод декомпозиции Холецкого, даже не смотря на то, что конечной целью процесса ортогонализации является построение матрицы Шмидта (это достигается обращением матрицы Холецкого в соответствии с (7)). Точность вычисления при переходе от X к H не должна падать существенно (для треугольной матрицы можно указать более короткий путь для обращения, чем традиционные вычисления алгебраических дополнений элементов; вычисление определителя сводится к перемножению диагональных элементов матрицы).
2. Метод сингулярного (спектрального) разложения несколько более трудоемок, чем метод Холецкого, но он имеет практическое преимущество, состоящее в возможности упорядочения спектра матрицы Грама в соответствии с потребностями исследователя. В частности, при использовании ортонормированного базиса для решения конкретных задач можно ограничивать размерность отрезка базиса гильбертова пространства более существенно, чем без возможности упорядочения. От этого зависит размерность разрешающей бесконечной системы уравнений при слабой корректировке суммы Бесселя (левая часть неравенства Бесселя) со всеми вытекающими отсюда последствиями.
Исследование выполнено при финансовой поддержке РФФИ и Липецкой области в рамках научных проектов № 19-41-480003 «р_а», № 19-48-480009 «р_а».